10 Bài tập Một số bài toán liên quan đến diện tích (có lời giải)

38 người thi tuần này 4.6 292 lượt thi 10 câu hỏi 45 phút

Đề số 1

🔥 Đề thi HOT:

2722 người thi tuần này

10 Bài tập Ứng dụng ba đường conic vào các bài toán thực tế (có lời giải)

7 K lượt thi 10 câu hỏi

1278 người thi tuần này

13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)

11.6 K lượt thi 13 câu hỏi

1097 người thi tuần này

12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)

6.1 K lượt thi 12 câu hỏi

485 người thi tuần này

185 câu Trắc nghiệm Toán 10 Bài 1:Phương trình đường thẳng trong mặt phẳng oxy có đáp án (Mới nhất)

5 K lượt thi 185 câu hỏi

325 người thi tuần này

16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án

7.2 K lượt thi 16 câu hỏi

302 người thi tuần này

10 Bài tập Các bài toán thực tế ứng dụng nhị thức Newton (có lời giải)

1.1 K lượt thi 10 câu hỏi

297 người thi tuần này

Bộ 5 đề thi cuối kì 2 Toán 10 Kết nối tri thức cấu trúc mới có đáp án - Đề 1

1.2 K lượt thi 21 câu hỏi

263 người thi tuần này

10 Bài tập Viết phương trình cạnh, đường cao, trung tuyến, phân giác của tam giác (có lời giải)

1.1 K lượt thi 10 câu hỏi

Nội dung liên quan:

15 câu Trắc nghiệm Toán 10 Kết nối tri thức Phương trình đường thẳng có đáp án

2852 lượt thi

1 đề

20 câu Trắc nghiệm Toán 10 Kết nối tri thức. Phương trình đường thẳng có đáp án (Phần 2)

2425 lượt thi

3 đề

10 Bài tập Xác định vectơ chỉ phương, vectơ pháp tuyến của đường thẳng, hệ số góc của đường thẳng (có lời giải)

584 lượt thi

1 đề

10 Bài tập Viết phương trình đường thẳng khi biết VTPT hoặc VTCP hoặc hệ số góc và 1 điểm đi qua (có lời giải)

383 lượt thi

1 đề

10 Bài tập Viết phương trình đường thẳng đi qua một điểm và vuông góc hoặc song song với một đường thẳng cho trước (có lời giải)

479 lượt thi

1 đề

10 Bài tập Viết phương trình cạnh, đường cao, trung tuyến, phân giác của tam giác (có lời giải)

415 lượt thi

1 đề

10 Bài tập Phương trình đoạn chắn của đường thẳng (có lời giải)

285 lượt thi

1 đề

15 câu Trắc nghiệm Toán 10 Kết nối tri thức Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách có đáp án

1538 lượt thi

1 đề

20 câu Trắc nghiệm Toán 10 Kết nối tri thức Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách. có đáp án (Phần 2)

2109 lượt thi

3 đề

10 Bài tập Vị trí tương đối giữa hai đường thẳng (có lời giải)

256 lượt thi

1 đề

Danh sách câu hỏi:

Câu 1

Trong mặt phẳng tọa độ Oxy, đường thẳng Δ: 5x + 3y – 15 = 0 tạo với các trục tọa độ một tam giác có diện tích bằng bao nhiêu?

A. 7,5;

B. 5;

C. 15;

D. 3.

Lời giải

Trong mặt phẳng tọa độ Oxy, đường thẳng Δ: 5x + 3y – 15 = 0 tạo với các trục tọa độ một tam giác (ảnh 1)

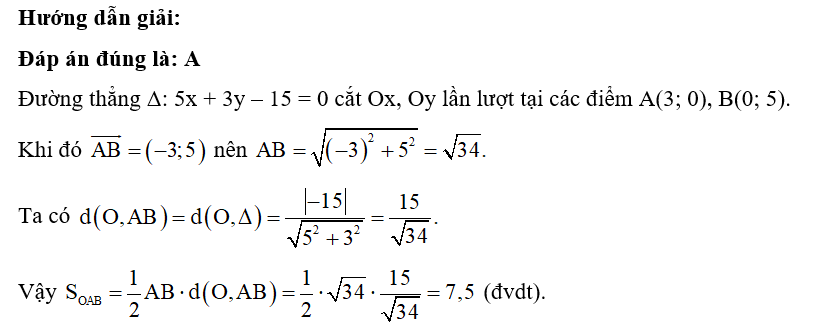
Câu 2

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC biết A(2; –1), B(1; 2) và C(2; –4). Diện tích tam giác ABC là

A. 4;

B. 2;

C. 3;

D. 1,5.

Lời giải

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC biết A(2; –1), B(1; 2) và C(2; –4). Diện tích tam giác ABC là (ảnh 1)

Câu 3

Trong mặt phẳng tọa độ Oxy, cho ba điểm A(3; –4), B(1; 5), C(3; 1). Diện tích tam giác ABC là

A. $\sqrt{26}$ ;

B. $2 \sqrt{5}$ ;

C. 10;

D. 5.

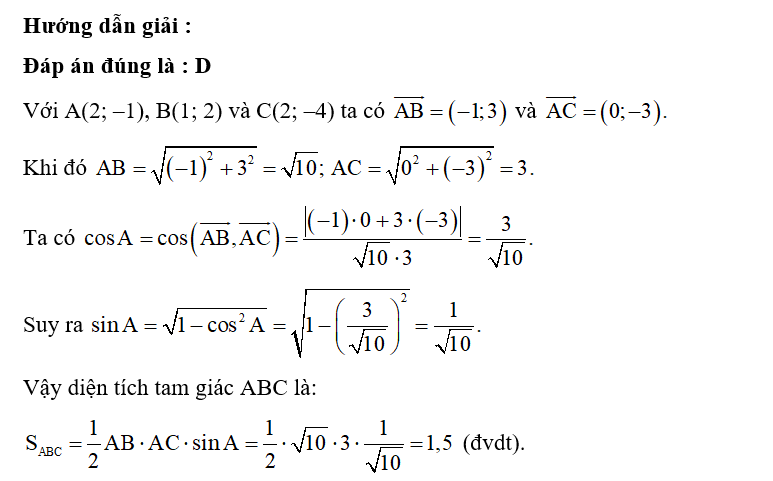
Lời giải

Hướng dẫn giải:

Đáp án đúng là: D

Ta có: $\vec{A C} = (0; 5) \Rightarrow {\vec{n}}_{A C} = (1; 0)$ là vectơ pháp tuyến của đường thẳng AC.

Từ $\vec{A C} = (0; 5)$ ta có $A C = \sqrt{0^{2} + 5^{2}} = 5.$

Phương trình đường thẳng AC là : x – 3 = 0.

Khi đó $d (B, A C) = \frac{|1 - 3|}{\sqrt{1^{2}}} = 2.$

Diện tích tam giác ABC là $S_{A B C} = \frac{1}{2} d (B, A C) \cdot A C = 5$ (đvdt).

Câu 4

Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d₁: mx – y – 4 = 0; d₂: –mx – y – 4 = 0. Gọi S là tập hợp các giá trị nguyên dương của m để tam giác tạo thành bởi d₁, d₂ và trục hoành có diện tích lớn hơn 8. Số phần tử của tập hợp S là

A. 1;

B. 3;

C. 2;

D. 4.

Lời giải

Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d1: mx – y – 4 = 0; d2: –mx – y – 4 = 0. (ảnh 1)

Câu 5

Trong mặt phẳng tọa độ Oxy, đường thẳng d đi qua điểm I(1; 3) và tạo với hai tia Ox, Oy một tam giác có diện tích bằng 6. Phương trình đường thẳng d nào sau đây không thỏa mãn điều kiện trên?

A. $(9 + 6 \sqrt{2}) x - y - 6 \sqrt{2} - 6 = 0$ ;

B. $(9 - 6 \sqrt{2}) x - y + 6 \sqrt{2} - 6 = 0$ ;

C. 3x – y + 6 = 0;

D. 3x + y – 6 = 0.

Lời giải

Trong mặt phẳng tọa độ Oxy, đường thẳng d đi qua điểm I(1; 3) và tạo với hai tia Ox, Oy một (ảnh 1)

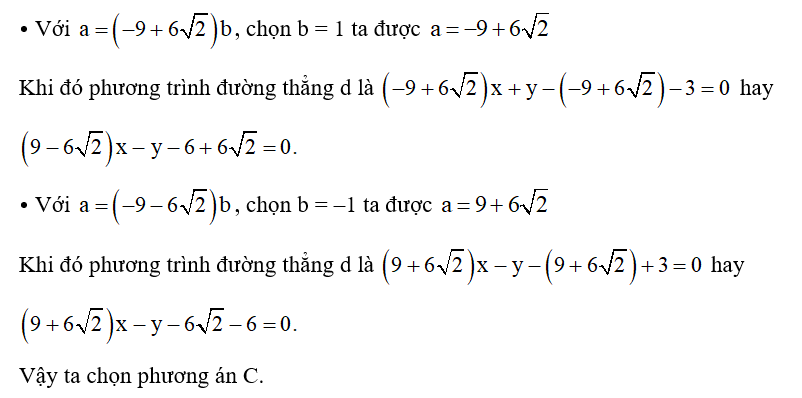
Trong mặt phẳng tọa độ Oxy, đường thẳng d đi qua điểm I(1; 3) và tạo với hai tia Ox, Oy một (ảnh 2)

Câu 6

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; –3), B(0; 2), C(–2; 4). Đường thẳng Δ đi qua A và chia tam giác ABC thành hai phần có diện tích bằng nhau. Phương trình của đường thẳng Δ là

A. 2x – y – 7 = 0;

B. x + y + 2 = 0;

C. x – 3y – 10 = 0;

D. 3x + y = 0.

Lời giải

Hướng dẫn giải:

Đáp án đúng là: D

Gọi I là giao điểm của đường thẳng Δ và BC.

Gọi H là hình chiếu của A trên BC.

Theo đề bài ta có: S_AIB= S_{AIC $\Leftrightarrow \frac{1}{2} . A H . I B = \frac{1}{2} . A H . I C \Leftrightarrow I B = I C$}. Suy ra I là trung điểm của đoạn thẳng BC.

Với B(0; 2), C(–2; 4) ta có I(–1; 3). Khi đó $\vec{A I} = (- 2; 6),$ suy ra ${\vec{n}}_{A I} = (3; 1)$ .

Đường thẳng Δ đi qua A(1; –3) và nhận vectơ ${\vec{n}}_{A I} = (3; 1)$ làm vectơ pháp tuyến nên có phương trình là 3(x – 1) + 1(y + 3) = 0 hay 3x + y = 0.

Câu 7

Trong mặt phẳng tọa độ Oxy, cho điểm M(2; 1). Đường thẳng d đi qua M, cắt các tia Ox, Oy lần lượt tại A và B (A, B khác O) sao cho tam giác OAB có diện tích nhỏ nhất. Phương trình đường thẳng d là

A. 2x – y – 3 = 0;

B. x – 2y = 0;

C. x + 2y – 4 = 0;

D. x – y – 1 = 0.

Lời giải

Trong mặt phẳng tọa độ Oxy, cho điểm M(2; 1). Đường thẳng d đi qua M, cắt các tia Ox, Oy lần lượt tại (ảnh 1)

Câu 8

Trong mặt phẳng tọa độ Oxy, đường thẳng d: $\frac{x}{a} + \frac{y}{b} = 1 (a, b \in ℤ; a, b \neq 0)$ đi qua M(–1; 6) và tạo với tia Ox, Oy một tam giác có diện tích bằng 4. Giá trị S = a + 2b có thể bằng

A. S = 6;

B. S = 8;

C. S = 10;

D. S = 12.

Lời giải

Trong mặt phẳng tọa độ Oxy, đường thẳng d: x/a + y/b = 1( a,b thuộc Z ; a,b khác 0) đi qua M(–1; 6) và tạo với tia Ox, Oy (ảnh 1)

Câu 9

Trong mặt phẳng tọa độ Oxy, cho đường thẳng d đi qua A(2; 1) có hệ số góc k nguyên dương. Phương trình đường thẳng d tạo với hai trục tọa độ một tam giác có diện tích bằng 0,5 là

A. x + y – 3 = 0;

B. x – y – 1 = 0;

C. 4x – y – 7 = 0;

D. x – 4y + 2 = 0.

Lời giải

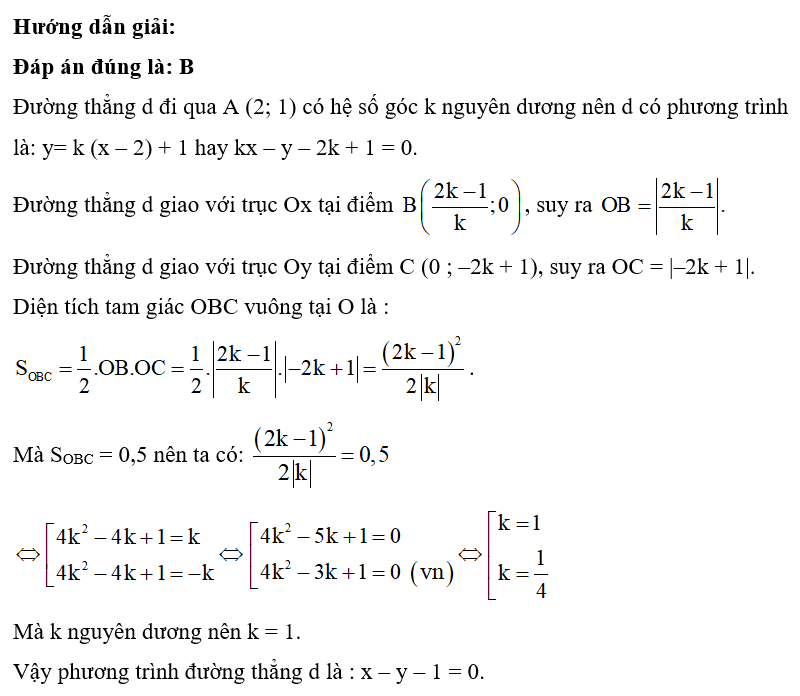
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d đi qua A(2; 1) có hệ số góc k nguyên dương. (ảnh 1)

Câu 10

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với A(1; –2), đường cao CH: x – y + 1 = 0, phân giác trong BN: 2x + y + 5 = 0. Diện tích tam giác ABC bằng

A. $\frac{45}{4}$ ;

B. $\frac{45}{2}$ ;

C. $\frac{41}{2}$ ;

D. $\frac{41}{4}$ .

Lời giải

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với A(1; –2), đường cao CH: x – y + 1 = 0 (ảnh 1)

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với A(1; –2), đường cao CH: x – y + 1 = 0 (ảnh 2)

4.6

58 Đánh giá

50%

40%

10 Bài tập Một số bài toán liên quan đến diện tích (có lời giải)

🔥 Đề thi HOT:

10 Bài tập Ứng dụng ba đường conic vào các bài toán thực tế (có lời giải)

13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)

12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)

185 câu Trắc nghiệm Toán 10 Bài 1:Phương trình đường thẳng trong mặt phẳng oxy có đáp án (Mới nhất)

16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án

10 Bài tập Các bài toán thực tế ứng dụng nhị thức Newton (có lời giải)

Bộ 5 đề thi cuối kì 2 Toán 10 Kết nối tri thức cấu trúc mới có đáp án - Đề 1

10 Bài tập Viết phương trình cạnh, đường cao, trung tuyến, phân giác của tam giác (có lời giải)

Nội dung liên quan:

15 câu Trắc nghiệm Toán 10 Kết nối tri thức Phương trình đường thẳng có đáp án

20 câu Trắc nghiệm Toán 10 Kết nối tri thức. Phương trình đường thẳng có đáp án (Phần 2)

10 Bài tập Xác định vectơ chỉ phương, vectơ pháp tuyến của đường thẳng, hệ số góc của đường thẳng (có lời giải)

10 Bài tập Viết phương trình đường thẳng khi biết VTPT hoặc VTCP hoặc hệ số góc và 1 điểm đi qua (có lời giải)

10 Bài tập Viết phương trình đường thẳng đi qua một điểm và vuông góc hoặc song song với một đường thẳng cho trước (có lời giải)

10 Bài tập Viết phương trình cạnh, đường cao, trung tuyến, phân giác của tam giác (có lời giải)

10 Bài tập Phương trình đoạn chắn của đường thẳng (có lời giải)

15 câu Trắc nghiệm Toán 10 Kết nối tri thức Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách có đáp án

20 câu Trắc nghiệm Toán 10 Kết nối tri thức Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách. có đáp án (Phần 2)

10 Bài tập Vị trí tương đối giữa hai đường thẳng (có lời giải)

Danh sách câu hỏi:

Trong mặt phẳng tọa độ Oxy, đường thẳng Δ: 5x + 3y – 15 = 0 tạo với các trục tọa độ một tam giác có diện tích bằng bao nhiêu?

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC biết A(2; –1), B(1; 2) và C(2; –4). Diện tích tam giác ABC là

Trong mặt phẳng tọa độ Oxy, cho ba điểm A(3; –4), B(1; 5), C(3; 1). Diện tích tam giác ABC là

Trong mặt phẳng tọa độ Oxy, đường thẳng d đi qua điểm I(1; 3) và tạo với hai tia Ox, Oy một tam giác có diện tích bằng 6. Phương trình đường thẳng d nào sau đây không thỏa mãn điều kiện trên?

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; –3), B(0; 2), C(–2; 4). Đường thẳng Δ đi qua A và chia tam giác ABC thành hai phần có diện tích bằng nhau. Phương trình của đường thẳng Δ là

Trong mặt phẳng tọa độ Oxy, cho điểm M(2; 1). Đường thẳng d đi qua M, cắt các tia Ox, Oy lần lượt tại A và B (A, B khác O) sao cho tam giác OAB có diện tích nhỏ nhất. Phương trình đường thẳng d là

Trong mặt phẳng tọa độ Oxy, đường thẳng d: xa+yb=1 a,b∈ℤ;a,b≠0 đi qua M(–1; 6) và tạo với tia Ox, Oy một tam giác có diện tích bằng 4. Giá trị S = a + 2b có thể bằng

Trong mặt phẳng tọa độ Oxy, cho đường thẳng d đi qua A(2; 1) có hệ số góc k nguyên dương. Phương trình đường thẳng d tạo với hai trục tọa độ một tam giác có diện tích bằng 0,5 là

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với A(1; –2), đường cao CH: x – y + 1 = 0, phân giác trong BN: 2x + y + 5 = 0. Diện tích tam giác ABC bằng

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Trong mặt phẳng tọa độ Oxy, đường thẳng d: $\frac{x}{a} + \frac{y}{b} = 1 (a, b \in ℤ; a, b \neq 0)$ đi qua M(–1; 6) và tạo với tia Ox, Oy một tam giác có diện tích bằng 4. Giá trị S = a + 2b có thể bằng