12 Bài tập Xác định hệ số a, b, c khi biết các tính chất của hàm số bậc hai (có lời giải)
46 người thi tuần này 4.6 847 lượt thi 12 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 3
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 2
Đề kiểm tra Ôn tập chương 9 (có lời giải) -Đề 1
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 3
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 2
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 1
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải:
Xét hàm số y = ax2 – 4x + c có b = – 4.
Đồ thị hàm số là parabol có bề lõm hướng xuống nên ta có: a < 0
Đồ thị có đỉnh S(–2; 7) nên ta có: \(\frac{{ - b}}{{2a}} = - 2 \Leftrightarrow \frac{{ - ( - 4)}}{{2a}} = - 2 \Leftrightarrow - 4a = 4 \Leftrightarrow a = - 1\) (thỏa mãn điều kiện).
Đồ thị cắt trục tung tại điểm (0; 3) nên ta có: c = 3
Vậy hàm số y = ax2 – 4x + c có a = –1; b = –4; c = 3.
Lời giải
Hướng dẫn giải:
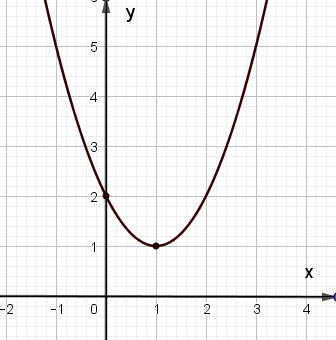
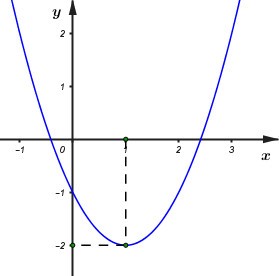
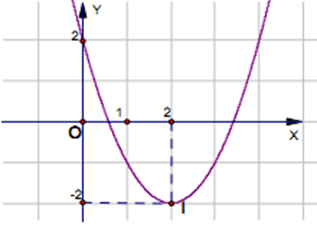
Dựa vào hình vẽ, ta thấy đồ thị hàm số y = ax2 + bx + c có bề lõm hướng lên, đỉnh S(1; 1) và cắt trục tung tại điểm (0; 2).
Do đó ta có:
a > 0 (1)
\( - \frac{b}{{2a}} = 1\) (2); \( - \frac{\Delta }{{4a}} = 1 \Leftrightarrow - \frac{{{b^2} - 4ac}}{{4a}} = 1\) (3)
c = 2 (4)
Thay (4) vào (3) ta có: \( - \frac{{{b^2} - 4a.2}}{{4a}} = 1 \Leftrightarrow - {b^2} + 8a = 4a \Leftrightarrow - {b^2} + 4a = 0\) (5)
Từ (2) ta có: b = –2a (6)
Thay (6) vào (5) ta có: –(–2a)2 + 4a = 0 ⇔ –4a2 + 4a = 0
⇔ 4a(–a + 1) = 0 ⇔ \(\left[ \begin{array}{l}a = 0\,\,(L)\\a = 1\,\,(TM)\end{array} \right.\)
Với a = 1 ta có: b = –2.1 = –2
Vậy hàm số y = ax2 + bx + c có a = 1, b = –2, c = 2.
Câu 3
Lời giải
Hướng dẫn giải:
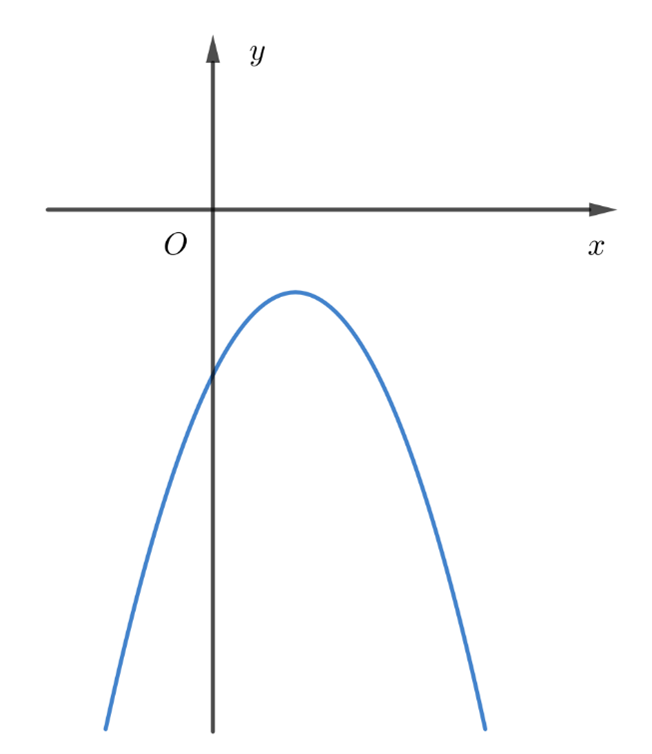
Đáp án đúng là: C.
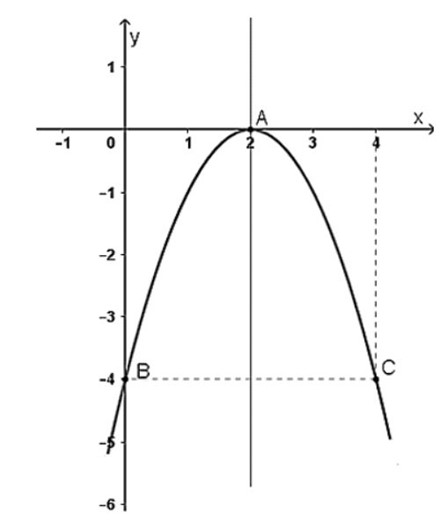
Ta thấy đồ thị hàm số có bề lõm hướng xuống, do đó a < 0.
Câu 4
Lời giải
Hướng dẫn giải:
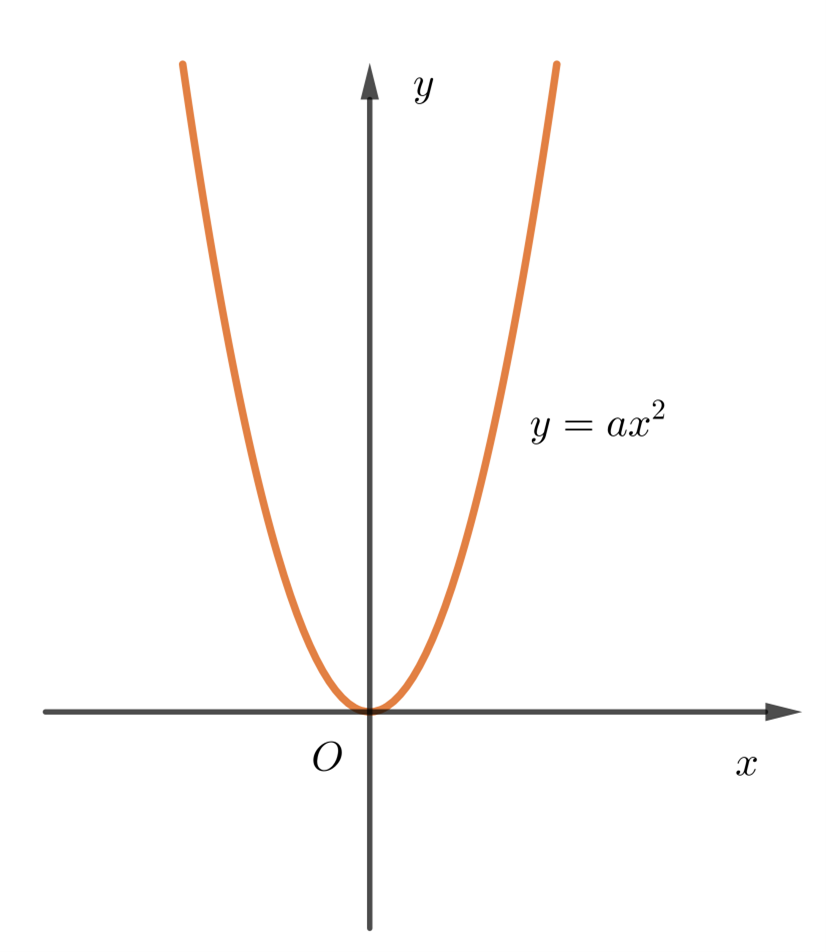
Đáp án đúng là: C.
Ta thấy đồ thị hàm số cắt trục tung tại điểm (0; 0) do đó c = 0.
Đồ thị có bề lõm hướng lên trên nên a > 0.
Câu 5
Lời giải
Hướng dẫn giải:
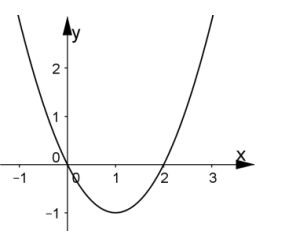
Đáp án đúng là: D.
Dựa vào đồ thị ta thấy
+ Đồ thị có bề lõm hướng lên trên nên a > 0.
+ Parabol cắt trục tung tại điểm (0; 0) nên c = 0.
+ Đỉnh của parabol có hoành độ là 1, lớn hơn 0 hay \( - \frac{b}{{2a}}\)> 0 và tung độ là – 1, nhỏ hơn 0 hay \( - \frac{\Delta }{{4a}}\)< 0.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.