15 câu Trắc nghiệm Toán 10 Kết nối tri thức Bài 8. Tổng và hiệu của hai vectơ có đáp án
38 người thi tuần này 4.6 2.5 K lượt thi 15 câu hỏi 30 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 3
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 2
Đề kiểm tra Ôn tập chương 9 (có lời giải) -Đề 1
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 3
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 2
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 1
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Danh sách câu hỏi:
Câu 1
A. Với ba điểm bất kì A, B, C ta có \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {BC} \);
B. Với ba điểm bất kì A, B, C ta có \(\overrightarrow {AB} + \overrightarrow {CB} = \overrightarrow {AC} \);
C. Với ba điểm bất kì A, B, C ta có \(\overrightarrow {AB} + \overrightarrow {CA} = \overrightarrow {BC} \);
D. Với ba điểm bất kì A, B, C ta có \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \).
Lời giải
Đáp án D
Quy tắc ba điểm được phát biểu như sau: Với ba điểm bất kì A, B, C ta có \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \).
Câu 2
A. \(\overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow {AB} \);
B. \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \);
C. \(\overrightarrow {IA} = - \overrightarrow {IB} \);
D. \(\overrightarrow {BA} + \overrightarrow {AC} = \overrightarrow {BC} \).
Lời giải
Đáp án A
Xét tam giác ABC, có:
\(\overrightarrow {BA} + \overrightarrow {AC} = \overrightarrow {BC} \) (quy tắc ba điểm). Do đó D đúng.
Vì G là trọng tâm tam giác nên \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \). Do đó B đúng.
Ta có I là trung điểm của AB nên \(\overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0 \) hay \(\overrightarrow {IA} = - \overrightarrow {IB} \). Do đó A sai và C đúng.
Câu 3
A. 5cm;
B. 10dm;
C. 10cm;
D. 15cm.
Lời giải
Đáp án đúng là C
Xét tam giác ABC vuông cân tại A có AH là đường cao nên AH là đường trung tuyến suy ra H là trung điểm của BC.
Gọi D là điểm đối xứng với A qua H.
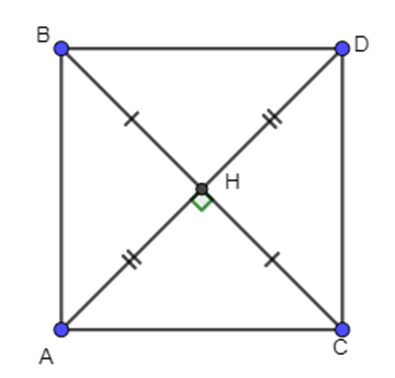
Xét tứ giác ABDC có AD cắt BC tại H là trung điểm của mỗi đường. Do đó ABDC là hình bình hành.
⇒ \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \) (quy tắc hình bình hành)
⇒ \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right|\)
Ta lại có hình bình hành ABDC có \(\widehat {BAC} = {90^0}\) nên ABDC là hình chữ nhật do đó AD = BC =10 cm.
⇒ \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD = BC = 10cm\).
Vậy độ dài \(\overrightarrow {AB} + \overrightarrow {AC} \) là 10 cm.
Câu 4
A. Mọi vectơ khác vectơ - không;
B. Không có vectơ nào ;
C. Chính nó;
D. Mọi vectơ kể cả vectơ – không.
Lời giải
Đáp án đúng là C
Vectơ \(\overrightarrow 0 \) được coi là vectơ đối của chính nó.
Câu 5
A. \(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {OC} - \overrightarrow {OD} \);
B. \(\overrightarrow {OB} - \overrightarrow {OA} = \overrightarrow {OC} - \overrightarrow {OD} \);
C. \(\overrightarrow {OA} - \overrightarrow {OD} = \overrightarrow {OC} - \overrightarrow {OB} \);
D. \(\overrightarrow {OA} - \overrightarrow {OC} = \overrightarrow {OD} - \overrightarrow {OB} \).
Lời giải
Đáp án đúng là B
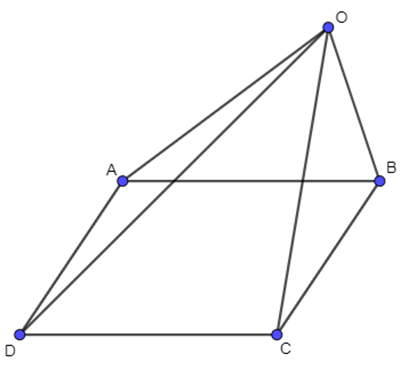
+) Áp dụng quy tắc hiệu ta có: \(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {BA} \) và \(\overrightarrow {OC} - \overrightarrow {OD} = \overrightarrow {DC} \):
\(\overrightarrow {OB} - \overrightarrow {OA} = \overrightarrow {AB} \) và \(\overrightarrow {OC} - \overrightarrow {OD} = \overrightarrow {DC} \);
Vì ABCD là hình bình hành nên AB = CD và AB // CD khi đó \(\overrightarrow {AB} = \overrightarrow {DC} \). Suy ra \(\overrightarrow {OA} - \overrightarrow {OB} \ne \overrightarrow {OC} - \overrightarrow {OD} \) và \(\overrightarrow {OB} - \overrightarrow {OA} = \overrightarrow {OC} - \overrightarrow {OD} \). Do đó B đúng, A sai.
+) Áp dụng quy tắc hiệu ta có: \(\overrightarrow {OA} - \overrightarrow {OD} = \overrightarrow {DA} \) và \(\overrightarrow {OC} - \overrightarrow {OB} = \overrightarrow {BC} \):
Vì ABCD là hình bình hành nên AD = CB và AD // CB khi đó \(\overrightarrow {DA} = \overrightarrow {CB} \). Suy ra \(\overrightarrow {OA} - \overrightarrow {OD} \ne \overrightarrow {OC} - \overrightarrow {OB} \). Do đó C sai.
+) Áp dụng quy tắc hiệu ta có: \(\overrightarrow {OA} - \overrightarrow {OC} = \overrightarrow {CA} \) và \(\overrightarrow {OD} - \overrightarrow {OB} = \overrightarrow {BD} \):
Vì hai vectơ \(\overrightarrow {CA} \) và \(\overrightarrow {BD} \) không cùng phương nên không bằng nhau. Suy ra\(\overrightarrow {OA} - \overrightarrow {OC} \ne \overrightarrow {OD} - \overrightarrow {OB} \). Do đó D sai.
Câu 6
A. 9,39 dm;
B. 3,06 dm;
C. 7,31 dm;
D. 2,70 dm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \);
B. \(\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \);
C. \(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow 0 \);
D. \(\overrightarrow {GC} + \overrightarrow {GO} = \overrightarrow 0 \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. \(\overrightarrow {PR} \);
B. \(\overrightarrow {MR} \);
C. \(\overrightarrow {MP} \);
D. \(\overrightarrow {MN} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. M là một điểm bất kì;
B. M là điểm thỏa mãn ACMD là hình bình hành;
C. M là điểm thỏa mãn ACDM là hình bình hành;
D. Không tồn tại điểm M.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. M là trung điểm của đoạn thẳng NP;
B. N là trung điểm của đoạn thẳng MP;
C. P là trung điểm của đoạn thẳng MN;
D. Cả A, B, C đều sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. 10N;
B. 4N;
C. 5,32N;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A. (900; 1 000);
B. (1 000; 1 100);
C. (1 100; 1 200);
D. (1 200; 1 300).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A. \(\left| {\overrightarrow a } \right| = 2\left| {\overrightarrow b } \right|\);
B. \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right|\);
C. \(\left| {\overrightarrow a } \right| = \sqrt 2 \left| {\overrightarrow b } \right|\);
D. \(\left| {\overrightarrow a } \right| = \frac{1}{{\sqrt 2 }}\left| {\overrightarrow b } \right|\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A. \[\frac{{\sqrt 2 a}}{2}\];
B. \[\sqrt 2 \]a;
C. \[\frac{{\sqrt 2 a}}{3}\];
D. a
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.