10 Bài tập So sánh hai mẫu số liệu tương đồng và xem xét mẫu nào ổn định hơn (có lời giải)
34 người thi tuần này 4.6 554 lượt thi 10 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 3
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 2
Đề kiểm tra Ôn tập chương 9 (có lời giải) -Đề 1
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 3
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 2
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 1
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Danh sách câu hỏi:
Câu 1
Lời giải
Hướng dẫn giải:
Đáp án đúng là: A.
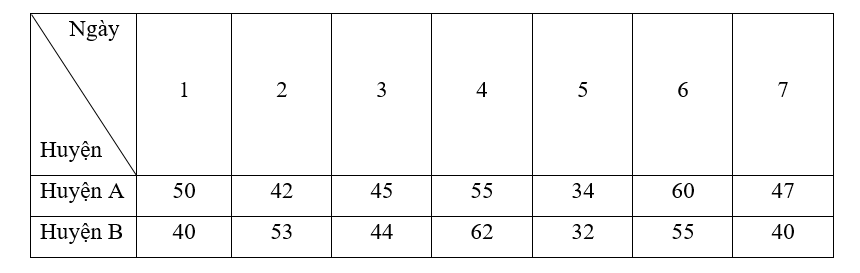
- Sắp xếp số lượng người tham gia hiến máu của huyện A trong 7 ngày theo thứ tự không giảm ta có:
34; 42; 45; 47; 50; 55; 60.
+ Giá trị nhỏ nhất của mẫu số liệu trên là 34.
+ Giá trị lớn nhất của mẫu số liệu trên là 60.
Suy ra khoảng biến thiên RA = 60 – 34 = 26.
Ta lại có:
+ Giá trị tứ phân vị thứ nhất là trung vị của mẫu: 34; 42; 45.
Do đó Q1A = 42.
+ Giá trị tứ phân vị thứ ba là trung vị của mẫu: 50; 55; 60.
Do đó Q3A = 55.
Suy ra khoảng tứ phân vị ∆QA = Q3A – Q1A = 55 – 42 = 13.
- Sắp xếp số lượng người tham gia hiến máu của huyện B trong 7 ngày theo thứ tự không giảm ta có:
32; 40; 40; 44; 53; 55; 62.
+ Giá trị nhỏ nhất của mẫu số liệu trên là 32.
+ Giá trị lớn nhất của mẫu số liệu trên là 62.
Suy ra khoảng biến thiên RB = 62 – 32 = 30.
Ta lại có:
+ Giá trị tứ phân vị thứ nhất là trung vị của mẫu: 32; 40; 40.
Do đó Q1B = 40.
+ Giá trị tứ phân vị thứ ba là trung vị của mẫu: 53; 55; 62.
Do đó Q3B = 55.
Suy ra khoảng tứ phân vị ∆QB = Q3B – Q1B = 55 – 40 = 15.
Ta thấy khoảng biến thiên và khoảng tứ phân vị trong số lượng người tham gia hiến máu của huyện A bé hơn huyện B nên số lượng người tham gia của huyện A ổn định hơn.
Câu 2
A. Huyện A;
Lời giải
Hướng dẫn giải:
Đáp án đúng là: A.
- Số trung bình lượng người tham gia hiến máu trong 7 ngày của huyện A là:
Công thức tính phương sai của một mẫu số liệu là:
S2 =
Thay số ta có:
= [(50 – 47,57)2 + (42 – 47,57)2 + (45 – 47,57)2 + (55 – 47,57)2 + (34 – 47,57)2 + (60 – 47,57)2 + (47 – 47,57)2] ≈ 62,53.
Do đó phương sai của mẫu số liệu trên là 62,53.
Độ lệch chuẩn của mẫu số liệu trên là SA = = ≈ 7,91.
- Số trung bình lượng người tham gia hiến máu trong 7 ngày của huyện B là:
Công thức tính phương sai của một mẫu số liệu là:
S2 =
Thay số ta có:
= [(40 – 46,57)2 + (53 – 46,57)2 + (44 – 46,57)2 + (62 – 46,57)2 + (32 – 46,57)2 + (55 – 46,57)2 + (40 – 46,57)2] ≈ 93,67.
Do đó phương sai của mẫu số liệu trên là 93,67.
Độ lệch chuẩn của mẫu số liệu trên là SB = = ≈ 9,68.
Ta thấy phương sai và độ lệch chuẩn trong số lượng người tham gia hiến máu của huyện A bé hơn huyện B nên số lượng người tham gia của huyện A ổn định hơn.
Câu 3
Lời giải
Hướng dẫn giải:
Đáp án đúng là: B.
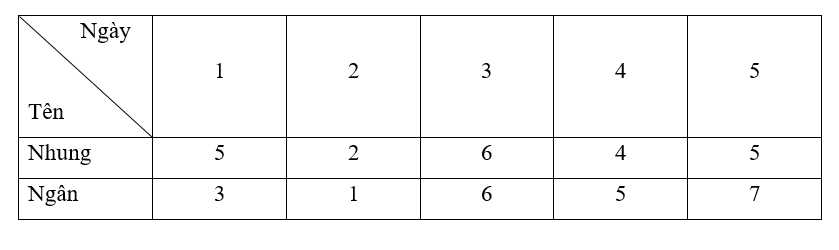
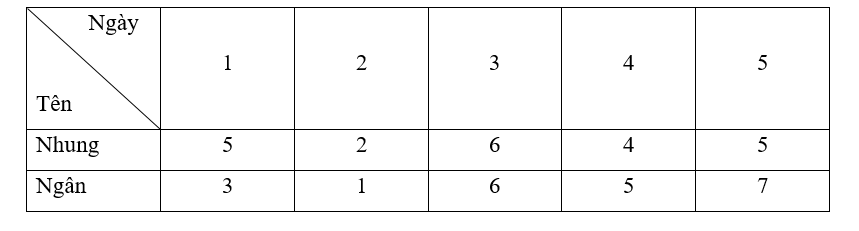
- Sắp xếp số giờ sử dụng Internet của bạn Nhung theo thứ tự không giảm ta có:
2; 4; 5; 5; 6.
+ Giá trị nhỏ nhất của mẫu số liệu trên là 2
+ Giá trị lớn nhất của mẫu số liệu trên là 6
Suy ra khoảng biến thiên R1 = 6 – 2 = 4.
Ta lại có:
+ Giá trị tứ phân vị thứ nhất là trung vị của mẫu: 2; 4.
Do đó Q1 =
+ Giá trị tứ phân vị thứ ba là trung vị của mẫu: 5; 6.
Do đó Q3 =
Suy ra khoảng tứ phân vị ∆Q1 = Q3 – Q1 = 5,5 – 3 = 2,5.
- Sắp xếp số giờ sử dụng Internet của bạn Ngân theo thứ tự không giảm ta có:
1; 3; 5; 6; 7.
+ Giá trị nhỏ nhất của mẫu số liệu trên là 1
+ Giá trị lớn nhất của mẫu số liệu trên là 7
Suy ra khoảng biến thiên R2 = 7 – 1 = 6.
Do đó của mẫu số liệu trên là 6.
Ta lại có:
+ Giá trị tứ phân vị thứ nhất là trung vị của mẫu: 1; 3.
Do đó Q1' =
+ Giá trị tứ phân vị thứ ba là trung vị của mẫu: 6; 7.
Do đó Q3' =
Suy ra khoảng tứ phân vị ∆Q2 = Q3' – Q1' = 6,5 – 2 = 4,5
Ta thấy khoảng biến thiên và khoảng tứ phân vị trong số giờ sử dụng Internet của bạn Nhung bé hơn Ngân nên số giờ sử dụng Internet của bạn Nhung ổn định hơn.
Câu 4
Lời giải
Hướng dẫn giải:
Đáp án đúng là: B.
- Số giờ trung bình sử dụng Internet của bạn Nhung là:
Công thức tính phương sai của một mẫu số liệu là:
S2 =
Thay số ta có:
= [(5 – 4,4)2 + (2 – 4,4)2 + (6 – 4,4)2 + (4 – 4,4)2 + (5 – 4,4)2] = 1,84.
Do đó phương sai của mẫu số liệu trên là 1,84.
Độ lệch chuẩn của mẫu số liệu trên là S1 = = ≈ 1,36.
- Số giờ trung bình sử dụng Internet của bạn Ngân là:
Công thức tính phương sai của một mẫu số liệu là:
S2 =
Thay số ta có:
= [(3 – 4,4)2 + (1 – 4,4)2 + (6 – 4,4)2 + (5 – 4,4)2 + (7 – 4,4)2] = 4,64.
Do đó phương sai của mẫu số liệu trên là 4,64.
Độ lệch chuẩn của mẫu số liệu trên là S2 = = ≈ 2,15.
Ta thấy phương sai và độ lệch chuẩn trong số giờ sử dụng Internet của bạn Nhung bé hơn Ngân nên số giờ sử dụng Internet của bạn Nhung ổn định hơn.
Câu 5
Lời giải
Hướng dẫn giải:
Đáp án đúng là: B.
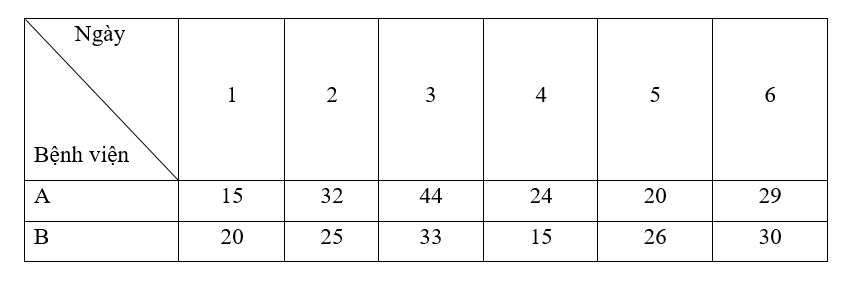
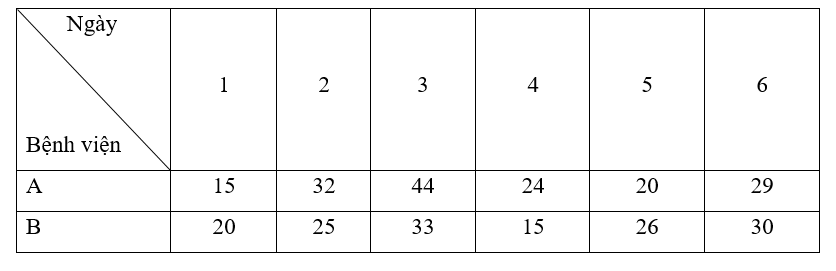
- Sắp xếp số lượng bệnh nhân khỏi bệnh của bệnh viện A theo thứ tự không giảm ta có:
15; 20; 24; 29; 32; 44.
+ Giá trị nhỏ nhất của mẫu số liệu trên là 15
+ Giá trị lớn nhất của mẫu số liệu trên là 44
Suy ra khoảng biến thiên RA = 44 – 15 = 29.
Ta lại có:
+ Giá trị tứ phân vị thứ nhất là trung vị của mẫu: 15; 20; 24.
Do đó Q1A = 20.
+ Giá trị tứ phân vị thứ ba là trung vị của mẫu: 29; 32; 44.
Do đó Q3A = 32.
Suy ra khoảng tứ phân vị ∆QA = Q3A – Q1A = 32 – 20 = 12.
- Sắp xếp số lượng bệnh nhân khỏi bệnh của bệnh viện B theo thứ tự không giảm ta có:
15; 20; 25; 26; 30; 33.
+ Giá trị nhỏ nhất của mẫu số liệu trên là 15
+ Giá trị lớn nhất của mẫu số liệu trên là 33
Suy ra khoảng biến thiên RB = 33 – 15 = 18.
Ta lại có:
+ Giá trị tứ phân vị thứ nhất là trung vị của mẫu: 15; 20; 25.
Do đó Q1B = 20.
+ Giá trị tứ phân vị thứ ba là trung vị của mẫu: 26; 30; 33.
Do đó Q3B = 30.
Suy ra ∆QB = Q3B – Q1B = 30 – 20 = 10.
Do đó khoảng tứ phân vị của mẫu số liệu trên là 10.
Ta thấy khoảng biến thiên và khoảng tứ phân vị trong số lượng bệnh nhân khỏi bệnh của bệnh viện B bé hơn bệnh viện A nên số lượng bệnh nhân khỏi bệnh của bệnh viện B ổn định hơn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.