Đề KSCL THCS Phú Diễn - HN_năm học 2025-2026_Tháng 12 có đáp án

1) Gọi chiều dài và chiều rộng ban đầu của khu vườn lần lượt là: \[x,{\rm{ }}y{\rm{ }}\left( m \right){\rm{ }}\left( {x,{\rm{ }}y > 1} \right).\]

Diện tích ban đầu của khu vườn là: \[xy{\rm{ }}\left( {{m^2}} \right)\]

Vì chiều dài của khu vườn sau khi tăng thêm 3m là \(x + 3\) (m) và chiều rộng của khu vườn sau

khi tăng thêm 2m là \(y + 2\) (m) thì diện tích khu vườn tăng 84m2 nên ta có phương trình: \(\left( {x + 3} \right)\left( {y + 2} \right) = xy + 84\) hay \(2x + 3y = 78\) (1)

Vì chiều dài, chiều rộng của khu vườn lúc sau khi đều giảm đi 1m lần lượt là \(x - 1\)(m), \(y - 1\)(m) 

thì diện tích khu vườn giảm đi 31m2 nên ta có phương trình:

\(\left( {x - 1} \right)\left( {y - 1} \right) = xy - 31\) hay \(x + y = 32\) (2)

Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}2x + 3y = 78\\x + y = 32\end{array} \right.\)       suy ra \(\left\{ \begin{array}{l}x = 18(tm)\\y = 14(tm)\end{array} \right.\).

Vậy chiều dài và chiều rộng ban đầu của khu vườn lần lượt là 18m, 14m.

2) Gọi số xe ban đầu đội vận chuyển đã chuẩn bị là: x (xe) (\[x \in {\mathbb{N}^*}\]).

Số tấn hàng trên mỗi xe theo như dự định của đội là: \(\frac{{36}}{x}\) (tấn/xe).

Trong thực tế số chiếc xe vận chuyển hàng của đội là: \(x + 3\) (xe).

Số tấn hàng trên mỗi xe trong thực tế của đội là: \(\frac{{36}}{{x + 3}}\) (tấn/xe).

Vì lượng hàng phải chở trên mỗi xe trong thực tế giảm xuống 1 tấn so với kế hoạch ban đầu nên

ta có phương trình: \(\frac{{36}}{x} - 1 = \frac{{36}}{{x + 3}}\) suy ra \[x =  - 12\] (ktm) hoặc \[x = 9\] (tm).

Vậy ban đầu đội vận chuyển đã chuẩn bị 9 xe.

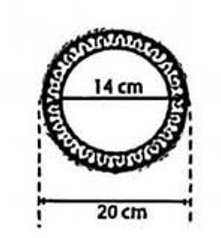
1) Bán kính đường tròn lớn là \(20:2 = 10\left( {cm} \right)\)

Bán kính đường tròn nhỏ là: \(14:2 = 7cm\)

Diện tích phần viền tráng men xanh của đĩa xứ là:

\(S = \pi \left( {{{10}^2} - {7^2}} \right) = 51\pi  \approx 51.3,14 = 160,14 \approx 160\left( {c{m^2}} \right)\)

2)

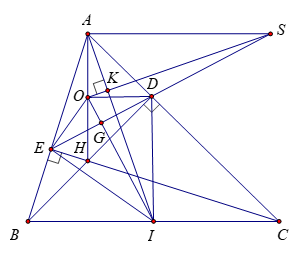
a) \(\Delta BEC\) vuông tại \(E\), có \(EI\) là đường trung tuyến ứng với cạnh huyền \(BC\), nên:

\(IE = IB = IC = \frac{1}{2}BC\)

\(\Delta BDC\) vuông tại \(D\), có \(DI\) là đường trung tuyến ứng với cạnh huyền \(BC\), nên:

\(ID = IB = IC = \frac{1}{2}BC\)

Do đó \(IB = IC = ID = IE\,\left( { = \frac{1}{2}BC} \right)\)

Vậy bốn điểm \(B\,,\,D\,,\,C\,,\,E\) cùng thuộc đường tròn tâm \(I\), đường kính \(BC\).

Xét \(\left( I \right)\), có \(DE\) là dây cung không đi qua tâm, do đó \(DE < BC\)

b) Xét \(\Delta ADB\) và \(\Delta AEC\), có: \(\widehat {ADB} = \widehat {AEC} = 90^\circ \) và \(\widehat {BAC}\) chung, nên  (g.g)

Suy ra \(\frac{{AD}}{{AE}} = \frac{{AB}}{{AC}} \Rightarrow AE.AB = AD.AC\)

\(\Delta ABC\) có hai đường cao \(BD\) và \(CE\) cắt nhau tại \(H\), nên \(H\) là trực tâm của \(\Delta ABC\)

Suy ra \(AH \bot BC\) \( \Rightarrow \widehat {ABC} + \widehat {BAH} = 90^\circ \) hay \(\widehat {IBE} + \widehat {OAE} = 90^\circ \)

Do \(IB = IE\left( { = \frac{1}{2}BC} \right)\) nên \(\Delta IBE\) cân tại \(I\) \( \Rightarrow \widehat {IEB} = \widehat {IBE}\)

\(\Delta AEH\) vuông tại \(E\), có \(EO\) là đường trung tuyến ứng với cạnh huyền \(AH\) nên \(OE = OA = OH = \frac{1}{2}AH\)

Do đó \(\Delta OAE\) cân tại \(O\) \( \Rightarrow \widehat {OEA} = \widehat {OAE}\)

Suy ra \(\widehat {IEB} + \widehat {OEA} = \widehat {IBE} + \widehat {OAE} = 90^\circ \) \( \Rightarrow \widehat {OEI} = 90^\circ \)

Vậy \(OE \bot EI\)

c) Chứng minh tương tự câu b, ta cũng có: \(OD \bot DI\)

\(\Delta ADH\) vuông tại \(D\), có \(DO\) là đường trung tuyến ứng với cạnh huyền nên: \(OD = OA = OH = \frac{1}{2}AH\)

Suy ra \(OD = OE\left( { = \frac{1}{2}AH} \right)\) nên \(O\) thuộc đường trung trực của \(DE\)

Mà \(ID = IE\left( { = \frac{1}{2}BC} \right)\) nên \(I\) thuộc đường trung trực của \(DE\)

Do đó \(OI\) là đường trung trực của \(DE\) hay \(OI \bot DE\)

Gọi \(G\) là giao điểm của \(OI\) và \(DE\); \(K\) là giao điểm của \(AI\) và \(OS\).

Ta có:  (g.g) \( \Rightarrow \frac{{OD}}{{OI}} = \frac{{OG}}{{OD}} \Rightarrow O{D^2} = OG.OI\)

 (g.g) \( \Rightarrow \frac{{OK}}{{OG}} = \frac{{OI}}{{OS}} \Rightarrow OK.OS = OG.OI\)

Do đó \(OK.OS = O{D^2} = O{A^2}\)\( \Rightarrow \frac{{OK}}{{OA}} = \frac{{OA}}{{OS}}\)

Xét \(\Delta OKA\) và \(\Delta OAS\), có: \(\frac{{OK}}{{OA}} = \frac{{OA}}{{OS}}\) và \(\widehat {AOS}\) chung

Do đó  (c.g.c)

\( \Rightarrow \widehat {OAS} = \widehat {OKA} = 90^\circ \) \( \Rightarrow SA \bot AO\) hay \(SA \bot AH\), mà \(AH \bot BC\) nên \(SA\,{\rm{//}}\,BC\) (đpcm)

Gọi số thiệp mẫu \(A\) và số thiệp mẫu \(B\) mà câu lạc bộ cần làm trong một ngày hội lần lượt là \(x\,,\,\,\,y\) (\[x\,,\,y \in \mathbb{N}*\] và \(x \le 200\), \(y \le 240\)).

Nếu chỉ làm thiệp mẫu \(B\), trong một giờ các bạn hoàn thành được \(60\) thiệp.

Vì thời gian làm một thiệp mẫu \(A\) gấp đôi thời gian làm một thiệp mẫu \(B\), nên nếu chỉ làm thiệp mẫu \(A\), trong một giờ các bạn hoàn thành được: \(60:2 = 30\) (thiệp).

Thời gian các bạn hoàn thành \(x\) thiệp mẫu \(A\) là \(\frac{x}{{30}}\) (giờ)

Thời gian các bạn hoàn thành \(y\) thiệp mẫu \(B\) là \(\frac{y}{{60}}\) (giờ)

Vì một ngày, câu lạc bộ có \(8\) giờ làm việc, nên ta có: \(\frac{x}{{30}} + \frac{y}{{60}} = 8\) (*)

Tiền lãi thu được khi bán hai loại thiệp chúc mừng là:

\(T = 24\,000x + 18\,000y = 6000\left( {4x + 3y} \right)\) (đồng)

Từ (*) suy ra \(2x + y = 480\) hay \(4x + 2y = 960\)

Ta có: \(4x + 3y = \left( {4x + 2y} \right) + y = 960 + y \le 960 + 240 = 1\,200\)

Nên \(T \le 6\,000.1\,200 = 7\,200\,000\)

Dấu “=” xảy ra khi và chỉ khi \(y = 240\) (thỏa mãn).

Khi đó: \(x = \frac{{480 - y}}{2} = \frac{{480 - 240}}{2} = 120\) (thỏa mãn).

Vậy trong một ngày hội, câu lạc bộ cần làm \(120\) thiệp mẫu \(A\) và \(240\) thiệp mẫu \(B\) để thu được tiền lãi cao nhất là \(7\,200\,000\) đồng.