Đề thi tuyển sinh vào lớp 10 Toán năm học 2021 - 2022 Sở GD&ĐT Đà Nẵng có đáp án

Ta có: \(A = \sqrt 4  + \sqrt 3 .\sqrt {12}  = \sqrt {{2^2}}  + \sqrt {3.12}  = 2 + \sqrt {36}  = 2 + 6 = 8.\)

Với \(x > 0;x \ne 4\) ta có:

\(B = \left( {\frac{{\sqrt x }}{{2 + \sqrt x }} + \frac{{x + 4}}{{4 - x}}} \right):\frac{x}{{x - 2\sqrt x }}\)

\(B = \left[ {\frac{{\sqrt x \left( {\sqrt x  - 2} \right)}}{{\left( {\sqrt x  + 2} \right).\left( {\sqrt x  - 2} \right)}} - \frac{{x + 4}}{{\left( {\sqrt x  + 2} \right).\left( {\sqrt x  - 2} \right)}}} \right]:\frac{x}{{\sqrt x \left( {\sqrt x  - 2} \right)}}\)

\(B = \frac{{x - 2\sqrt x  - x - 4}}{{\left( {\sqrt x  + 2} \right).\left( {\sqrt x  - 2} \right)}} \cdot \frac{{\sqrt x \left( {\sqrt x  - 2} \right)}}{x}\)

\(B = \frac{{ - 2\left( {\sqrt x  + 2} \right)}}{{\left( {\sqrt x  + 2} \right).\left( {\sqrt x  - 2} \right)}} \cdot \frac{{\sqrt x \left( {\sqrt x  - 2} \right)}}{x} = \frac{{ - 2}}{{\sqrt x }}.\)

Vậy với \(x > 0;x \ne 4\) thì \(B = \frac{{ - 2}}{{\sqrt x }}.\)

Xét \(B <  - \sqrt x \)\( \Leftrightarrow \frac{{ - 2}}{{\sqrt x }} <  - \sqrt x \)\( \Leftrightarrow  - 2 <  - x \Leftrightarrow x < 2\)

Mà \(x \in \mathbb{Z}\) và \(x > 0;x \ne 4\) nên \(x = 1.\)

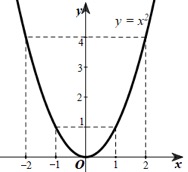
a) * Vẽ đồ thị \(\left( P \right):y = {x^2}\)  

Hàm số \(\left( P \right):y = {x^2}\) có hệ số \(a = 1 > 0\) nên hàm số đồng biến khi \(x > 0\) và nghịch biến khi \(x < 0\) và đồ thị hàm số có bề lõm quay lên, nhận trục \(Oy\) làm trục đối xứng.
Ta có bảng giá trị sau:

Vậy đồ thị \(\left( P \right)\) là parabol đi qua các điểm \(\left( { - 2;4} \right),\left( { - 1;2} \right),\left( {0;0} \right),\left( {1;1} \right),\left( {2;4} \right)\).

* Chứng minh rằng \(\left( d \right)\) luôn đi qua điểm \(C\left( {2;4} \right).\)

Giả sử \(C\left( {2;4} \right) \in \left( d \right)\)

\( \Leftrightarrow {y_C} = k.{x_C} - 2k + 4\)

\( \Leftrightarrow 4 = k.2 - 2k + 4\)

\( \Leftrightarrow 4 = 4\) (luôn đúng với mọi \(k\))

Vậy \(\left( d \right)\) luôn đi qua điểm \(C\left( {2;4} \right)\) với mọi \(k\).

b)

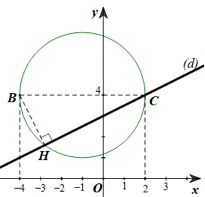
Ta có: \(H\) là hình chiếu của điểm \(B\left( { - 4;4} \right)\) trên \(\left( d \right)\)

\( \Rightarrow BH \bot HC\) (vì \(C \in \left( d \right)\))

\( \Rightarrow \Delta HBC\) vuông tại \(H\)

Áp dụng định lí Pythagore cho tam giác \(HBC\) vuông tại \(H\), ta có:

\(B{C^2} = B{H^2} + H{C^2}\)

 Có: \({S_{BHC}} = \frac{1}{2}.BH.HC\)

Áp dụng bất đẳng thức \(a.b \le \frac{{{a^2} + {b^2}}}{2}\) với hai số không âm \(a,b\), ta được:

\({S_{BHC}} = \frac{1}{2}.BH.HC \le \frac{1}{2}.\frac{{B{H^2} + C{H^2}}}{2} = \frac{{B{C^2}}}{4}\)   \(\left( 1 \right)\)

Mà \(BC = \left| {{x_C} - {x_B}} \right| = \left| {2 - \left( { - 4} \right)} \right| = \left| 6 \right| = 6\)       \(\left( 2 \right)\)

Thay \(\left( 2 \right)\) vào \(\left( 1 \right)\) ta được: \({S_{BHC}} \le 9{\rm{  }}(c{m^2})\)

Dấu “=” xảy ra khi và chỉ khi \(\left\{ {\begin{array}{*{20}{c}}{BH = HC}\\{B{H^2} + H{C^2} = B{C^2} = 36}\end{array}} \right. \Leftrightarrow BH = HC = 3\sqrt 2 \)

Vậy khi \(k\) thay đổi \(\left( {k \ne 0} \right)\) thì diện tích tam giác \(HBC\) không vượt quá \(9c{m^2}\).

a) Với \(m = 2\) thì phương trình \(\left( * \right)\) trở thành:

\({x^2} + 4x - 12 = 0\)

\( \Leftrightarrow {x^2} + 6x - 2x - 12 = 0\)

\( \Leftrightarrow x\left( {x + 6} \right) - 2\left( {x + 6} \right) = 0\)

\( \Leftrightarrow \left( {x + 6} \right)\left( {x - 2} \right) = 0\)

\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x + 6 = 0}\\{x - 2 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - 6}\\{x = 2}\end{array}} \right.\)

Vậy với \(m = 2\) thì phương trình \(\left( * \right)\) có tập nghiệm là \(S = \left\{ { - 6;2} \right\}\).

b) Phương trình \(\left( * \right)\) có \(a.c = 1.\left( { - 12} \right) = - 12 < 0\) nên luôn có hai nghiệm phân biệt trái dấu \({x_1},{x_2}\).

Theo định lí Vi-et ta có: \(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = - 4m + 4}\\{{x_1}.{x_2} = - 12}\end{array}} \right.\)   \(\left( 1 \right)\)

Vì \({x_2}\) là nghiệm của phương trình \(\left( * \right)\) nên ta có: \(x_2^2 + 4\left( {m - 1} \right){x_2} - 12 = 0\)

\( \Leftrightarrow x_2^2 + 4m{x_2} - 4{x_2} - 12 = 0\)

\( \Leftrightarrow x_2^2 + 4\left( {m{x_2} - 4} \right) - 4{x_2} + 4 = 0\)

\( \Leftrightarrow 4\left( {4 - m{x_2}} \right) = x_2^2 - 4{x_2} + 4\)

\( \Leftrightarrow 4\left( {4 - m{x_2}} \right) = {\left( {{x_2} - 2} \right)^2}\)

\( \Leftrightarrow 2.\sqrt {4 - m{x_2}} = \sqrt {{{\left( {{x_2} - 2} \right)}^2}} \)

\( \Leftrightarrow 2.\sqrt {4 - m{x_2}} = \left| {{x_2} - 2} \right|\)          \(\left( 2 \right)\)

Mà theo bài có: \(4\left| {{x_1} - 2} \right|.\sqrt {4 - m{{\rm{x}}_2}} = {\left( {{x_1} + {x_2} - {x_1}{x_2} - 8} \right)^2}\) \(\left( 3 \right)\)

Thay \(\left( 1 \right)\),\(\left( 2 \right)\) vào \(\left( 3 \right)\) ta được: \(2.\left| {{x_1} - 2} \right|.\left| {{x_2} - 2} \right| = {\left( { - 4m + 4 + 12 - 8} \right)^2}\)

\( \Leftrightarrow 2.\left| {\left( {{x_1} - 2} \right)\left( {{x_2} - 2} \right)} \right| = {\left( {8 - 4m} \right)^2}\)

\( \Leftrightarrow 2.\left| {{x_1}{x_2} - 2\left( {{x_1} + {x_2}} \right) + 4} \right| = {4^2}.{\left( {2 - m} \right)^2}\)

\( \Leftrightarrow 2.\left| { - 12 - 2\left( { - 4m + 4} \right) + 4} \right| = 16{\left( {m - 2} \right)^2}\)

\( \Leftrightarrow 2.\left| { - 16 + 8m} \right| = 16{\left( {m - 2} \right)^2}\)

\( \Leftrightarrow 16.\left| {m - 2} \right| = 16{\left( {m - 2} \right)^2}\)

\( \Leftrightarrow \left| {m - 2} \right| = {\left( {m - 2} \right)^2}\)

\( \Leftrightarrow {\left( {m - 2} \right)^2} = {\left( {m - 2} \right)^4}\)

\( \Leftrightarrow {\left( {m - 2} \right)^4} - {\left( {m - 2} \right)^2} = 0\)

\( \Leftrightarrow {\left( {m - 2} \right)^2}.\left[ {{{\left( {m - 2} \right)}^2} - 1} \right] = 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{{\left( {m - 2} \right)}^2} = 0}\\{{{\left( {m - 2} \right)}^2} - 1 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m - 2 = 0}\\{{{\left( {m - 2} \right)}^2} = 1}\end{array}} \right.\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m - 2 = 0}\\{m - 2 = 1}\\{m - 2 = - 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 2}\\{m = 3}\\{m = 1}\end{array}} \right.\)

Vậy \(m \in \left\{ {1;2;3} \right\}\).

rrow {x^2} + 1000x - 750000 = 0\)

\( \Leftrightarrow {x^2} + 1500x - 500x - 750000 = 0\)

\( \Leftrightarrow x\left( {x + 1500} \right) - 500\left( {x + 1500} \right) = 0\)

\( \Leftrightarrow \left( {x + 1500} \right)\left( {x - 500} \right) = 0\)

\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x + 1500 = 0}\\{x - 500 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - 1500\left( {ktm} \right)}\\{x = 500\left( {tm} \right)}\end{array}} \right.\)

Vậy theo kế hoạch, địa phương này cần \(\frac{{12000}}{{500}} = 24\) (giờ) để xét nghiệm xong.

a) Gọi số lớn là \(x\)\(\left( {x > 15,x \in \mathbb{N}} \right)\), số bé là \(y\)\(\left( {y \in \mathbb{N}} \right)\).

Tổng của hai số là 2021 nên ta có phương trình: \(x + y = 2021\)  \(\left( 1 \right)\)

Hiệu của số lớn và số bé bằng 15 nên ta có phương trình: \(x - y = 15\) \(\left( 2 \right)\)

Từ \(\left( 1 \right)\),\(\left( 2 \right)\) ta có hệ phương trình:

\(\left\{ {\begin{array}{*{20}{c}}{x + y = 2021}\\{x - y = 15}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{2x = 2036}\\{y = x - 15}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 1018}\\{y = 1003}\end{array}} \right.\left( {tm} \right)\)

Vậy số lớn là 1018, số bé là 1003.