Đề thi tuyển sinh vào lớp 10 Toán năm học 2022 - 2023 Sở GD&ĐT Đà Nẵng có đáp án

\(A = \sqrt 9  + \sqrt {16}  + 2\sqrt 2  - \sqrt 8 \)

\( = \sqrt {{3^2}}  + \sqrt {{4^2}}  + 2\sqrt 2  - \sqrt {{2^2}.2} \)

\( = 3 + 4 + 2\sqrt 2  - 2\sqrt 2 \)

\( = 7\).

Với \(x \ge 0,x \ne 1\) ta có:

\(B = \left( {\frac{{\sqrt x }}{{\sqrt x  + 1}} + \frac{1}{{\sqrt x  - 1}}} \right):\frac{{x + 1}}{{x - 1}}\)

\( = \frac{{\sqrt x \left( {\sqrt x  - 1} \right) + \sqrt x  + 1}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}:\frac{{x + 1}}{{x - 1}}\)

\( = \frac{{x - \sqrt x  + \sqrt x  + 1}}{{x - 1}}.\frac{{x - 1}}{{x + 1}}\)

\( = \frac{{x + 1}}{{x + 1}} = 1\).

Vậy với \(x \ge 0,x \ne 1\) thì \(B = 1\).

a) • Vẽ đồ thị hàm số \(y =  - {x^2}\)

Hàm số có hệ số \(a =  - 1 < 0\) nên hàm số đồng biến khi \(x < 0\), nghịch biến khi \(x > 0\)

Do đó đồ thị hàm số \(y =  - {x^2}\) là parabol có bề lõm quay xuống dưới.

Bảng giá trị:

Vậy parabol \(y =  - {x^2}\) đi qua các điểm \(\left( { - 2; - 4} \right),\left( { - 1; - 1} \right);\left( {0;0} \right),\left( {1; - 1} \right),\left( {2; - 4} \right)\).

• Vẽ đồ thị hàm số \(y = 2x - 3\):

Bảng giá trị:

Vậy đồ thị hàm số \(y = 2x - 3\) là đường thẳng đi qua hai điểm \(\left( {0; - 3} \right)\) và \(\left( {\frac{3}{2};0} \right)\).

Ta có đồ thị hàm số \(y =  - {x^2}\) và \(y = 2x - 3\) trên cùng một mặt phẳng tọa độ như sau:

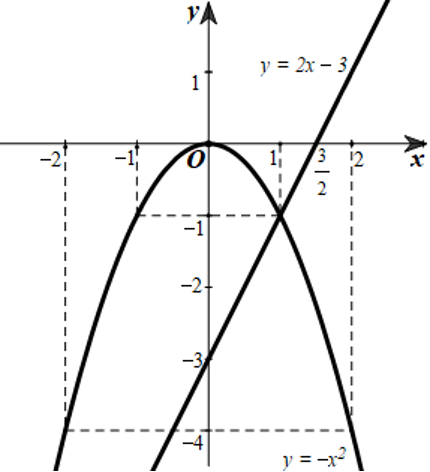
b) Xét phương trình hoành độ giao điểm của đồ thị hàm số \(y =  - {x^2}\) và \(y = 2x - 3\):

\( - {x^2} = 2x - 3\)

\( \Leftrightarrow {x^2} + 2x - 3 = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}x = 1\\x =  - 3\end{array} \right.\)

Với \(x = 1 \Rightarrow y =  - 1\)

Với \(x =  - 3 \Rightarrow y =  - 9\)

Do đó giao điểm của hai đồ thị đó là \(A\left( {1; - 1} \right),B\left( { - 3; - 9} \right)\).

Gọi \(H,K\) lần lượt là hình chiếu vuông góc của \(A,B\) trên trục \(Ox\).

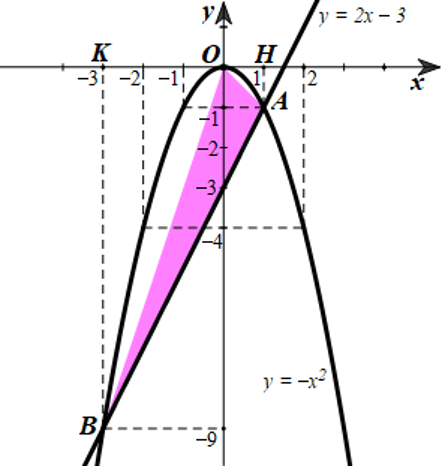
\({S_{ABKH}} = \frac{{\left( {AH + BK} \right).HK}}{2} = \frac{{\left( {1 + 9} \right).4}}{2} = 20\left( {c{m^2}} \right)\)

\({S_{OAH}} = \frac{1}{2}OH.AH = \frac{1}{2}.1.1 = \frac{1}{2}\left( {c{m^2}} \right)\)

\({S_{OBK}} = \frac{1}{2}OK.BK = \frac{1}{2}.3.9 = \frac{{27}}{2}\left( {c{m^2}} \right)\)

Vậy \({S_{OAB}} = {S_{ABKH}} - {S_{OAH}} - {S_{OBK}} = 20 - \frac{1}{2} - \frac{{27}}{2} = 6\,\,\left( {c{m^2}} \right)\).

Ta có: \(\left\{ \begin{array}{l}x - 3y = 5\\2x + 3y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x = 6\\y = \frac{{1 - 2x}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y =  - 1\end{array} \right.\)

Vậy hệ phương trình đã cho có nghiệm duy nhất \(\left( {x;y} \right) = \left( {2; - 1} \right)\).

Đổi 20 phút = \(\frac{1}{3}\) giờ.

Gọi vận tốc ban đầu của xe máy là \(x\left( {km/h} \right)\left( {x > 0} \right)\).

Vận tốc lúc sau của xe máy là \(x + 8\left( {km/h} \right)\).

Thời gian xe máy dự định đi hết quãng đường AB là \(\frac{{160}}{x}\) (giờ).

Quãng đường xe đi được sau 2 giờ là \(2x(km)\).

Quãng đường còn lại là: \(160 - 2x\left( {km} \right)\).

Thời gian xe đi với vận tốc \(x + 8(km/h)\) là \(\frac{{160 - 2x}}{{x + 8}}\) (giờ).

Do xe máy đến \(B\) đúng thời gian quy định nên ta có phương trình:

\(\frac{{160}}{x} = 2 + \frac{1}{3} + \frac{{160 - 2x}}{{x + 8}}\)

\( \Leftrightarrow \frac{{160}}{x} - \frac{{160 - 2x}}{{x + 8}} = \frac{7}{3}\)

\( \Leftrightarrow \frac{{160x + 1280 - 160x + 2{x^2}}}{{{x^2} + 8x}} = \frac{7}{3}\)

\( \Leftrightarrow \frac{{1280 + 2{x^2}}}{{{x^2} + 8x}} = \frac{7}{3}\)

\( \Leftrightarrow 6{x^2} + 3840 = 7{x^2} + 56x\)

\( \Leftrightarrow {x^2} + 56x - 3840 = 0\)

\( \Leftrightarrow {x^2} - 40x + 96x - 3840 = 0\)

\( \Leftrightarrow x\left( {x - 40} \right) + 96\left( {x - 40} \right) = 0\)

\( \Leftrightarrow \left( {x - 40} \right)\left( {x + 96} \right) = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}x = 40(tm)\\x =  - 96(ktm)\end{array} \right.\)

Vậy vận tốc ban đầu của xe máy là \(40(km/h)\).