Đề thi tuyển sinh vào lớp 10 Toán năm học 2023 - 2024 Sở GD&ĐT TP.HCM có đáp án

a) Xét hàm số \(\left( d \right):y = x + 4\)

Ta có bảng giá trị

                                                                                                            Xét hàm số \(\left( P \right):y = \frac{{{x^2}}}{2}\)

Ta có bảng giá trị

                                                                                                            (0,25 điểm)

Đồ thị hàm số \(\left( P \right)\) và \(\left( d \right)\):

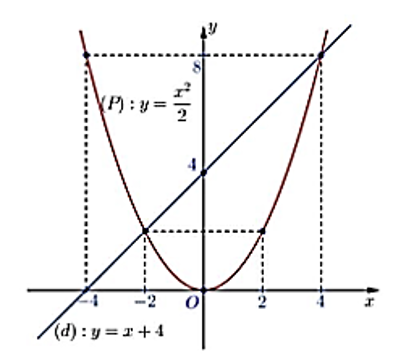
 (0,5 điểm)

b) Phương trình hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là \(\frac{{{x^2}}}{2} = x + 4\)

\( \Leftrightarrow \frac{{{x^2}}}{2} - x - 4 = 0 \Leftrightarrow {x^2} - 2x - 8 = 0\)

\( \Leftrightarrow \left( {x - 4} \right)\left( {x + 2} \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x =  - 2\\x = 4\end{array} \right.\)                                                     (0,25 điểm)

+ Với \(x =  - 2\) thì \(y =  - 2 + 4 = 2\).                                                     (0,25 điểm)

+ Với \(x = 4\) thì \(y = 4 + 4 = 8\).                                                           (0,25 điểm)

Vậy tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là \(\left( { - 2;\,2} \right)\) và \(\left( {4;\,8} \right)\).

Vì phương trình đã cho có 2 nghiệm là \({x_1},{x_2}\) nên theo định lý Vi-ét, ta có:

\(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - b}}{a} = \frac{{13}}{2}\\{x_1}.{x_2} = \frac{c}{a} = \frac{{ - 6}}{2} =  - 3\end{array} \right.\).                                                                   (0,5 điểm)

Ta có:

\(A = \left( {{x_1} + {x_2}} \right)\left( {{x_1} + 2{x_2}} \right) - x_2^2\)

\( = x_1^2 + 2{x_1}{x_2} + {x_2}{x_1} + 2x_2^2 - x_2^2\)

\( = x_1^2 + x_2^2 + 3{x_1}{x_2}\)

\( = {\left( {{x_1} + {x_2}} \right)^2} + {x_1}{x_2}\)                                                                            (0,25 điểm)

\( = {\left( {\frac{{13}}{2}} \right)^2} + \left( { - 3} \right) = \frac{{157}}{4}\).                                                                  (0,25 điểm)

Vậy \(A = \frac{{157}}{4}\).

a) Đổi 1,58 m = 158 cm.

Thay \(T = 158\) và \(N = 2\) vào \(M = T - 100 - \frac{{T - 150}}{N}\), ta có:

\(M = 158 - 100 - \frac{{158 - 150}}{2} = 54\) (kg).

Vậy cân nặng lý tưởng của bạn Hạnh là 54 kg.                                           (0,25 điểm)

b) Thay \(M = 68\) và \(N = 4\) vào \(M = T - 100 - \frac{{T - 150}}{N}\), ta có:

\(68 = T - 100 - \frac{{T - 150}}{4}\)\( \Leftrightarrow \frac{{4T - \left( {T - 150} \right)}}{4} = 168\)\( \Leftrightarrow 3T + 150 = 672\)           (0,25 điểm)

\( \Leftrightarrow 3T = 522 \Leftrightarrow T = 174\) (cm).                                                                      (0,25 điểm)

Vậy để cân nặng của Phúc là lý tưởng thì chiều cao của bạn Phúc cần đạt là 174 cm hay 1,74 m.

- Nếu mua nhiều hơn 10 bông hồng thì từ bông thứ 11 trở đi mỗi bông được giảm thêm 10% trên giá niêm yết, do đó giá mỗi bông hồng từ bông hồng thứ 11 đến 20 là:

15 000 . (100% – 10%) = 13 500 (đồng).

- Nếu mua nhiều hơn 20 bông hồng thì từ bông thứ 21 trở đi mỗi bông được giảm thêm 20% trên giá đã giảm, do đó giá mỗi bông hồng từ bông hồng thứ 21 là:

13 500 . (100% – 20%) = 10 800 (đồng).

a) Nếu khách hàng mua 30 bông hồng thì số tiền phải trả là:

15 000 . 10 + 13 500 . 10 + 10 800 . 10 = 393 000 (đồng).     (0,25 điểm)

b) Vì số tiền bạn Thảo phải trả là 555 000 > 393 000 (đồng) nên bạn đã mua nhieuf hơn 30 bông hồng.

Gọi \(x\) là số bông hồng mà bạn Thảo đã mua \(\left( {x \in \mathbb{N},x > 30} \right)\).

Ta có:

\(15000.10 + 13500.10 + 10800\left( {x - 20} \right) = 555000\)                           (0,25 điểm)

\( \Leftrightarrow x = 45\) (nhận).                                                                               (0,25 điểm)

Vậy bạn Thảo đã mua 45 bông hồng.

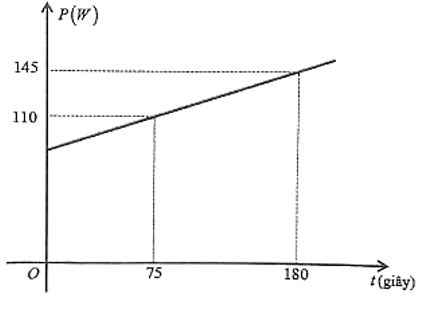
a) Quan sát đồ thị ta thấy:

Tại thời điểm \(t = 75\) (giây) thì công suất hao phí là \(110W\) nên đồ thị hàm số \(P = at + b\) đi qua điểm \(\left( {75;\,110} \right)\). Ta có phương trình: \(110 = 75a + b\). (1)

Tại thời điểm \(t = 180\) (giây) thì công suất hao phí là \(145\,W\) nên đồ thị hàm số \(P = at + b\) đi qua điểm \(\left( {180;\,145} \right)\). Ta có phương trình: \(145 = 180a + b\). (2)

Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}110 = 75a + b\\145 = 180a + b\end{array} \right.\)                                 (0,25 điểm)

\( \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{3}\\b = 85\end{array} \right.\).                                                                                                (0,25 điểm)

Vậy các hệ số cần tìm là \(a = \frac{1}{3},\,b = 85\).

b) Từ câu a) ta có: \(P = \frac{1}{3}t + 85\). Gọi \({t_0}\) (giây) là thời gian đun nước với công suất hao phí là \(P\left( {{t_0}} \right) = 105\,W\), ta có phương trình

\(\frac{1}{3}{t_0} + 85 = 105\)                  (0,25 điểm)

\( \Leftrightarrow {t_0} = 60\).                             (0,25 điểm)

Vậy thời gian để đun nước với công suất hao phí \(105\left( W \right)\) là 60 giây.