20 câu Trắc nghiệm Toán 10 Cánh diều Bài 1. Hàm số và đồ thị (Đúng-sai, trả lời ngắn) có đáp án
31 người thi tuần này 4.6 285 lượt thi 20 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 3
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 2
Đề kiểm tra Ôn tập chương 9 (có lời giải) -Đề 1
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 3
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 2
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 1
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Danh sách câu hỏi:
Câu 1
A. \(\mathbb{R}\backslash \left\{ 1 \right\}\).
B. \(\mathbb{R}\backslash \left\{ 3 \right\}\).
C. \(\mathbb{R}\backslash \left\{ 2 \right\}\).
D. \(\left( {1; + \infty } \right)\).
Lời giải
Đáp án đúng là: A
Điều kiện xác định: \[2x - 2 \ne 0 \Leftrightarrow x \ne 1\].
Nên tập xác định của hàm số là \[D = \mathbb{R}\backslash \left\{ 1 \right\}\].
Câu 2
A. \(y = \frac{{2\sqrt x }}{{{x^2} + 4}}\).
B. \(y = {x^2} - \sqrt {{x^2} + 1} - 3\).
C. \(y = \frac{{3x}}{{{x^2} - 4}}\).
D. \(y = {x^2} - 2\sqrt {x - 1} - 3\).
Lời giải
Đáp án đúng là: B
\(y = \frac{{2\sqrt x }}{{{x^2} + 4}}\) có tập xác định là \(\left( {0;\,\, + \infty } \right)\).
\(y = \frac{{3x}}{{{x^2} - 4}}\) có tập xác định là \(\mathbb{R}\backslash \left\{ { - 2;\,\,2} \right\}\).
\(y = {x^2} - 2\sqrt {x - 1} - 3\) có tập xác định là \(\left[ {1;\,\, + \infty } \right)\).
Câu 3
A. \(m \le - 4\).
B. \(m < - 4\).
C. \(m > 0\).
D. \(m < 4\).
Lời giải
Đáp án đúng là: B
Hàm số \(y = \frac{{2x + 1}}{{{x^2} - 2x - 3 - m}}\) xác định trên \(\mathbb{R}\) khi phương trình \({x^2} - 2x - 3 - m = 0\) vô nghiệm hay \(\Delta ' = m + 4 < 0 \Leftrightarrow m < - 4\).
Câu 4
A. Hàm số nghịch biến trên khoảng \(\left( {0; + \infty } \right)\).
B. Hàm số vừa đồng biến, vừa nghịch biến trên khoảng \(\left( {0; + \infty } \right)\).
C. Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\).
D. Hàm số không đồng biến, không nghịch biến trên khoảng \(\left( {0; + \infty } \right)\).
Lời giải
Đáp án đúng là: A
\(\begin{array}{l}\forall {x_1},\,{x_2} \in \left( {0; + \infty } \right):\,{x_1} \ne {x_2}\\f\left( {{x_2}} \right) - f\left( {{x_1}} \right) = \frac{3}{{{x_2}}} - \frac{3}{{{x_1}}} = \frac{{ - 3\left( {{x_2} - {x_1}} \right)}}{{{x_2}{x_1}}} \Rightarrow \frac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} = - \frac{3}{{{x_2}{x_1}}} < 0\end{array}\)
Vậy hàm số nghịch biến trên khoảng \(\left( {0; + \infty } \right)\).
Câu 5
A. \(\left( { - 2;0} \right)\).
B. \(\left( {1;1} \right)\).
C. \(\left( { - 2; - 12} \right)\).
D. \(\left( {1; - 1} \right)\).
Lời giải
Đáp án đúng là: A
Thay tọa độ điểm vào hàm số ta thấy chỉ có điểm \(\left( { - 2;0} \right)\) thỏa mãn.
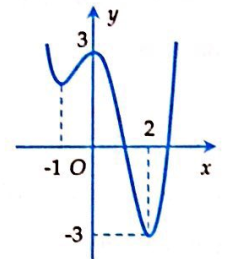
Câu 6
A. Hàm số đồng biến trên khoảng \(\left( {0;2} \right)\).
B. Hàm số nghịch biến trên khoảng \(\left( { - 3;0} \right)\).
C. Hàm số đồng biến trên khoảng \(\left( { - 1;0} \right)\).
D. Hàm số nghịch biến trên khoảng \(\left( {0;3} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. 0.
B. \(\frac{9}{2}\).
C. \(\frac{{ - 9}}{2}\).
D. \(\frac{3}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. \[x + y = \frac{{7\sqrt 2 }}{2}\].
B. \[x + y = \frac{{3\sqrt 2 }}{2}\].
C. \[x + y = \frac{{\sqrt 2 }}{2}\].
D. \[x + y = \frac{{5\sqrt 2 }}{2}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. \(f\left( 3 \right) = 36\).
B. \(f\left( 3 \right) = 18\).
C. \(f\left( 3 \right) = 29\).
D. \(f\left( 3 \right) = 25\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho một tấm nhôm hình vuông cạnh 6 cm. Người ta muốn cắt một hình thang như hình vẽ. Tìm tổng \(x + y\) để diện tích hình thang\[EFGH\] đạt giá trị nhỏ nhất. (ảnh 1)](https://video.vietjack.com/upload2/images/1753790873/1753790942-image2.png)