Bộ 10 đề thi giữa kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 10
33 người thi tuần này 4.6 7.2 K lượt thi 13 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải
a) Đúng. Phương trình \[\left( * \right)\] có các hệ số là \[a = 2\,;\,\,b = - 5\,;\,\,c = 1.\]
b) Sai. Để phương trình có dạng \[ax + by = c\] là phương trình bậc nhất hai ẩn thì \(a \ne 0\) hoặc \(b \ne 0.\)
Do đó, phương trình \[\left( * \right)\] là phương trình bậc nhất hai ẩn \[x,{\rm{ }}y\] vì \(a = 2 \ne 0\); \(b = - 5 \ne 0.\)
c) Sai. Thay \[x = 0\,;{\rm{ }}y = 5\] vào phương trình \[\left( * \right)\], ta được: \[4 \cdot 0 - 7 \cdot 5 = --\,35 \ne - 1.\]
Do đó cặp số \[\left( {0\,;\,\,5} \right)\] không phải là nghiệm của phương trình \[\left( * \right)\].
d) Đúng. Ta có \[4x - 7y = - 1\] suy ra \[7y = 4x + 1\] nên \[y = \frac{4}{7}x + \frac{1}{7}\].
Do đó, biểu diễn hình học tất cả các nghiệm của phương trình \[\left( * \right)\] là đường thẳng \[y = \frac{4}{7}x + \frac{1}{7}.\]
Câu 2
A. \(x \ne 2.\)
B. \(x \ne - 1.\)
C. \[x \ne 2\] và \(x \ne - 1.\)
D. \(x \ne 2\) và \(x \ne 0.\)
Lời giải
Vì \(x - 2 \ne 0\) khi \(x \ne 2\) và \(x + 1 \ne 0\) khi \(x \ne - 1\) nên ĐKXĐ của phương trình \[\frac{1}{{x - 2}} + \frac{x}{{x + 1}} = - \frac{1}{2}\] là \[x \ne 2\] và \(x \ne - 1.\)
Câu 3
A. \[2x + y \le 8\].
B. \[0x - 2 < 0\].
C. \[{x^2} - 5x + 4 > 0.\]
D. \[\frac{2}{3}x--1 \ge 5.\]
Lời giải
Bất phương trình có dạng \[ax + b < 0\] (hoặc \[ax + b > 0\,;\,\,ax + b \le 0\,;\,\,ax + b \ge 0\,)\] trong đó \[a\,,\,\,b\] là hai số đã cho, \(a \ne 0\) được gọi là bất phương trình bậc nhất một ẩn \(x.\)</>
Bất phương trình \[2x + y \le 8\] có hai ẩn \(x\,,\,\,y\) nên không phải là bất phương trình bậc nhất một ẩn.
Bất phương trình \[0x - 2 < 0\] có dạng \[ax + b \le 0\] và \(a = 0\) nên không phải là bất phương trình bậc nhất một ẩn.
Bất phương trình \[{x^2} - 5x + 4 > 0\] có vế trái là đa thức bậc hai, vế phải là 0 nên không phải là bất phương trình bậc nhất một ẩn.
Ta có \[\frac{2}{3}x--1 \ge 5\] hay \[\frac{2}{3}x--6 \ge 0\]. Bất phương trình \[\frac{2}{3}x--6 \ge 0\] có dạng \[ax + b \ge 0\] và \(a = 2\) nên là bất phương trình bậc nhất một ẩn.
Vậy chọn đán án D.
Câu 4
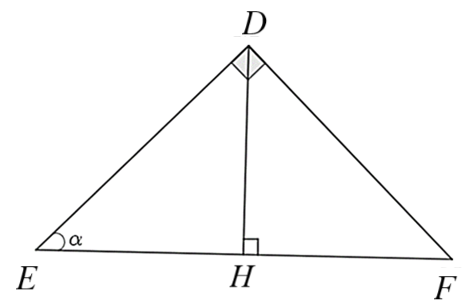
A. \(\frac{{EH}}{{DH}}\).
B. \(\frac{{DH}}{{EF}}\).
C. \(\frac{{DF}}{{EF}}\).
D. \(\frac{{DH}}{{EH}}\).
Lời giải
Đáp án đúng là: A
Xét \(\Delta DEF\) vuông tại \[D,\] ta có:
\(\cot E = \frac{{EH}}{{DH}}\) hay \(\cot \alpha = \frac{{EH}}{{DH}}.\)
Vậy chọn đáp án A.
Câu 5
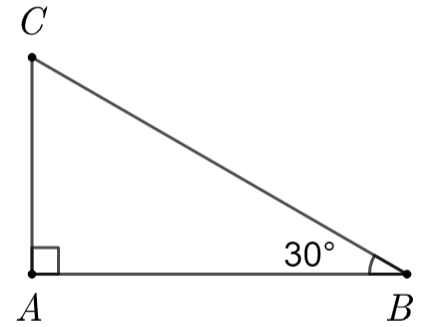
A. \(\frac{{\sqrt 3 }}{2}.\)
B. \(\frac{1}{2}\).
C. \(\frac{{\sqrt 2 }}{2}.\)
D. 1.
Lời giải
Đáp án đúng là: B
|
Tam giác \[ABC\] có cạnh huyền \(BC\) nên tam giác \[ABC\] vuông tại \[A\] nên \(\sin B = \frac{{AC}}{{BC}}\). Suy ra \[\frac{{AC}}{{BC}} = \sin 30^\circ = \frac{1}{2}.\] Vậy tỉ số giữa cạnh đối \(AC\) và cạnh huyền \(BC\) bằng \[\frac{1}{2}.\] |
|
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.