Đề kiểm tra Khảo sát sự biến thiên và vẽ đồ thị của hàm số (có lời giải) - Đề 1
92 người thi tuần này 4.6 893 lượt thi 22 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Câu 1
Lời giải
Câu 2
Lời giải
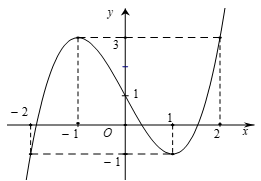
Đồ thị trên là đồ thị hàm bậc \(3\) có \(a < 0\). Suy ra chọn đáp án C.
Câu 3
Lời giải
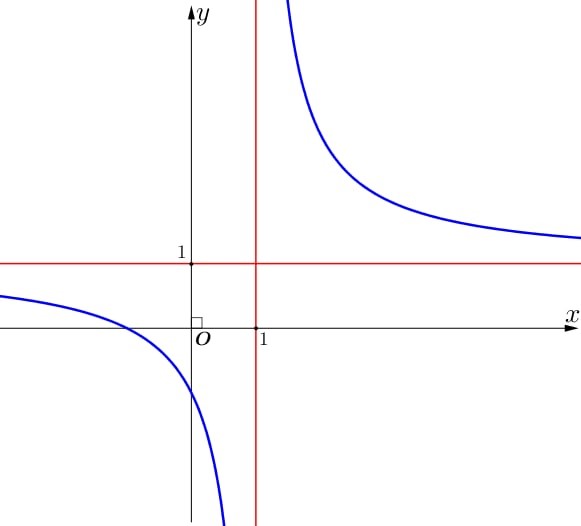
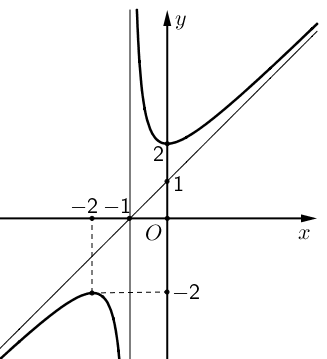
Ta có đồ thị hàm số có tiệm cận đứng \(x = 1\), nên loại A, B.
Đồ thị hàm số có tiệm cận ngang \(y = 1\) nên chọn D.
Vì \[\mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} \left( {\frac{{x + 1}}{{x - 1}}} \right) = - \infty \] và \[\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \left( {\frac{{x + 1}}{{x - 1}}} \right) = + \infty \].
Câu 4
Lời giải
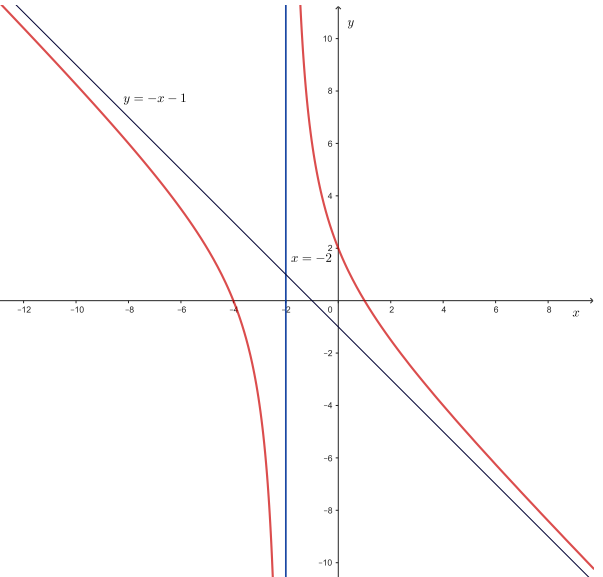
Ta có đồ thị hàm số có tiệm cận đứng \(x = - 2\), nên loại B; D là hàm số bậc \(3\)nên loại D; đồ thị của C có tiệm cận đứng, không có tiệm cận xiên nên loại C.
Đồ thị hàm số có tiệm cận xiên \(y = - x - 1\) nên chọn#A.
Vì \(a = \mathop {\lim }\limits_{x \to + \infty } \frac{{f\left( x \right)}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - {x^2} - 3x + 4}}{{{x^2} + 2x}} = - 1\).
\(b = \mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - ( - 1)x} \right] = \mathop {\lim }\limits_{x \to + \infty } \left[ {\frac{{ - {x^2} - 3x + 4}}{{x + 2}} - ( - 1)x} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - x + 4}}{{x + 2}} = - 1\)
Đồ thị hàm số có tiệm cận xiên là đường thẳng \(y = - x - 1\).
Câu 5
Lời giải
Ta có: \(\mathop {\lim }\limits_{x \to - {3^ + }} y = \mathop {\lim }\limits_{x \to - {3^ + }} \frac{{2x - 1}}{{x + 3}}\)\( = - \infty \); \(\mathop {\lim }\limits_{x \to - {3^ - }} y\)\( = \mathop {\lim }\limits_{x \to - {3^ - }} \frac{{2x - 1}}{{x + 3}} = + \infty \).
\( \Rightarrow x = - 3\) là đường tiệm cận đứng của đồ thị hàm số.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI
Học sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh chọn đúng hoặc sai.
Cho hàm số \[y = \frac{1}{3}{x^3} - 2{x^2} + mx + 1\].
a) Hàm số đồng biến trên \[\mathbb{R}\] khi \[m = 5\].
b) Hàm số có cực trị khi \[m = 5\].
c) Để hàm số có \[2\] cực trị thì \[m < 4\].
d) Khi \[m \ge 4\]thì hàm số đồng biến trên \[\left( {1,4} \right)\].
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI
Học sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh chọn đúng hoặc sai.Cho hàm số \[y = \frac{1}{3}{x^3} - 2{x^2} + mx + 1\].
a) Hàm số đồng biến trên \[\mathbb{R}\] khi \[m = 5\].
b) Hàm số có cực trị khi \[m = 5\].
c) Để hàm số có \[2\] cực trị thì \[m < 4\].
d) Khi \[m \ge 4\]thì hàm số đồng biến trên \[\left( {1,4} \right)\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
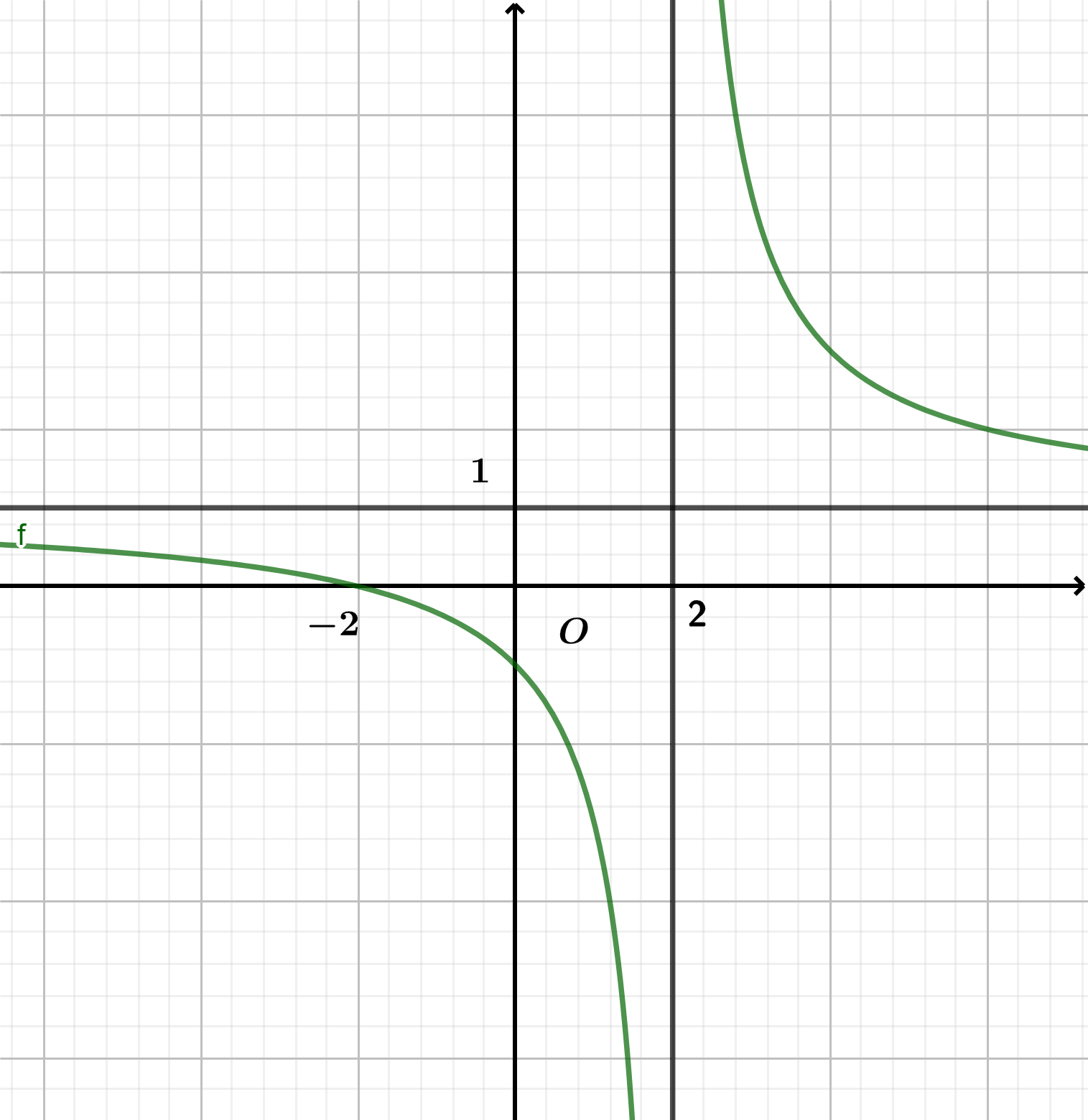
![Cho hàm số hữu tỉ \[y = ax + 2 + \frac{b}{{x + c}}\] có đồ thị như hình bên dưới. Tính\(P = a + b + c.\) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/12-1759200440.png)
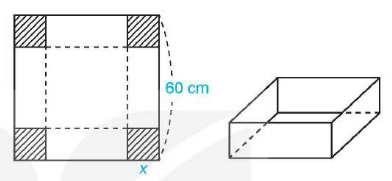
![Hai cột đỡ dọc \[MN\] và \[PQ\] ( song song với trục \[Oy\]) là đoạn nối giữa khung của Parabol và đường \[XY\]. Tính tổng độ d (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/14-1759200516.png)