Đề kiểm tra Khảo sát sự biến thiên và vẽ đồ thị của hàm số (có lời giải) - Đề 4
44 người thi tuần này 4.6 893 lượt thi 22 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Lời giải
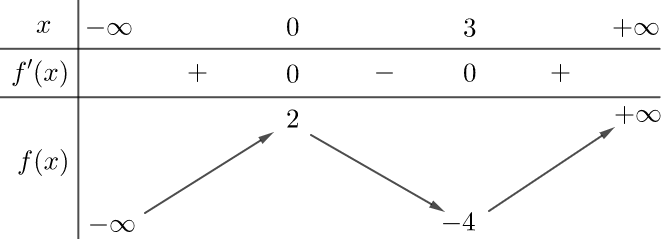
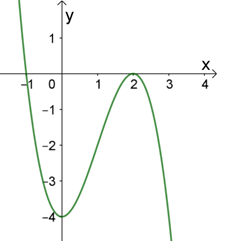
Đây là dáng điệu của hàm số bậc 3 nên ta loại \(y = {x^4} + 3{x^2} + 2\) và \(y = \frac{{x + 1}}{{x - 2}}\).
Từ bảng biến thiên ta có \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = - \infty \) và \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( {{x^3} - 3{x^2} + 2} \right) = + \infty ;\)
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {{x^3} - 3{x^2} + 2} \right) = - \infty \) nên đáp án \(y = {x^3} - 3{x^2} + 2\) thỏa mãn.
Câu 2
Lời giải
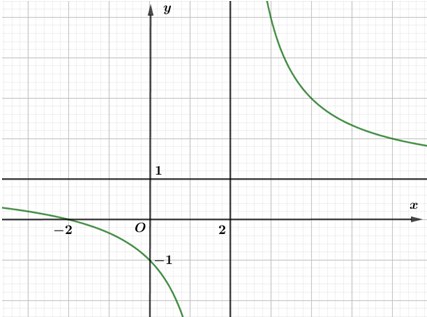
+) Đồ thị hàm số \(y = \frac{{x - 2}}{{x + 2}}\) có tiệm cận đứng là \[x = - 2\]. Loại A
+) Đồ thị hàm số \(y = \frac{{2x + 4}}{{x - 2}}\) có tiệm cận ngang là \[y = 2\]. Loại B
+) Đồ thị hàm số \(y = \frac{{x + 1}}{{x - 2}}\) cắt trục tung tại điểm có tung độ bằng \( - \frac{1}{2}\). Loại C.
+) Đồ thị hàm số \(y = \frac{{x + 2}}{{x - 2}}\) có tiệm cận ngang là \[y = 1\], tiệm cận đứng \[x = 2\], cắt trục hoành tại điểm có hành độ bằng \[ - 2\] và cắt trục tung tại điểm có tung độ bằng \[ - 1\]. Chọn D.
Câu 3
Lời giải
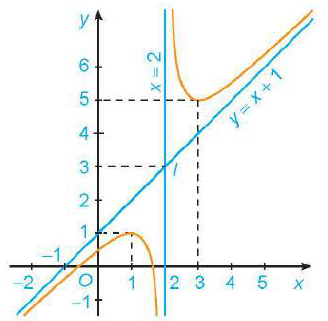
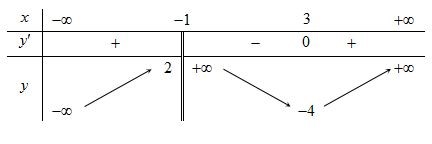
Căn cứ vào đồ thị ta có:
Đồ thị hàm số có tiệm cận đứng \(x = 2\).
Đồ thị hàm số có tiệm cận xiên \(y = x + 1\).
\(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = - \infty \).
Tọa độ giao điểm của đồ thị \(y = f\left( x \right)\) và trục \(Ox\) là \(A\left( {{x_0};0} \right)\) với \(0 < {x_0} < 1\).
Câu 4
Lời giải
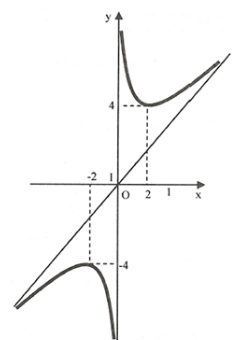
+) Đồ thị hàm số \(y = \frac{{x - 1}}{{x + 1}}\) không có tiệm cận xiên. Loại A
+) Đồ thị hàm số \(y = {x^4} - 2{x^2}\) không có tiệm cận xiên. Loại B
+) Đồ thị hàm số \(y = {x^3} - 3{x^2}\) không có tiệm cận xiên. Loại D
+) Đồ thị hàm số \(y = \frac{{{x^2} + 4}}{x}\) có tiệm cận xiên là \[y = x\], tiệm cận đứng \[x = 0\]. Chọn C.
Câu 5
Cho hàm số \[y = \frac{{2x - 4}}{{x - 1}}\] . Tọa độ giao điểm của đồ thị và trục \[Oy\] là
Lời giải
Cho \[x = 0\], ta được \[y = \frac{{2.0 - 4}}{{0 - 1}} = 4\]. Tọa độ giao điểm với trục \[Oy\] là \(\left( {0;4} \right)\).
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI
Học sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh chọn đúng hoặc sai.
Cho hàm số \[y = {x^3} - 3x + 2\]. Khi đó
a) Tập xác định của hàm số đã cho là \[\left( {0\,;\, + \infty } \right)\].
b) Đồ thị của hàm số đã cho đi qua điểm \[\left( {0\,;2} \right)\].
c) Hàm số đạt cực trị tại \[x = 0\].
d) Giá trị lớn nhất của hàm số đã cho trên đoạn \[\left[ {0;2} \right]\] bằng \[4\].
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI
Học sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh chọn đúng hoặc sai.
Cho hàm số \[y = {x^3} - 3x + 2\]. Khi đó
a) Tập xác định của hàm số đã cho là \[\left( {0\,;\, + \infty } \right)\].
b) Đồ thị của hàm số đã cho đi qua điểm \[\left( {0\,;2} \right)\].
c) Hàm số đạt cực trị tại \[x = 0\].
d) Giá trị lớn nhất của hàm số đã cho trên đoạn \[\left[ {0;2} \right]\] bằng \[4\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.