Đề kiểm tra Khảo sát sự biến thiên và vẽ đồ thị của hàm số (có lời giải) - Đề 3
45 người thi tuần này 4.6 893 lượt thi 22 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Câu 1
Lời giải
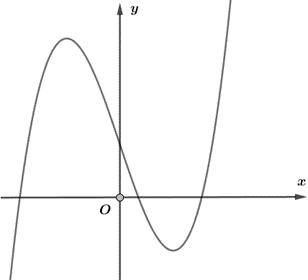
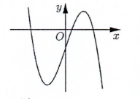
Đồ thị trên là đồ thị hàm bậc ba, và \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty \,\, \Rightarrow a > 0\).
Câu 2
Lời giải
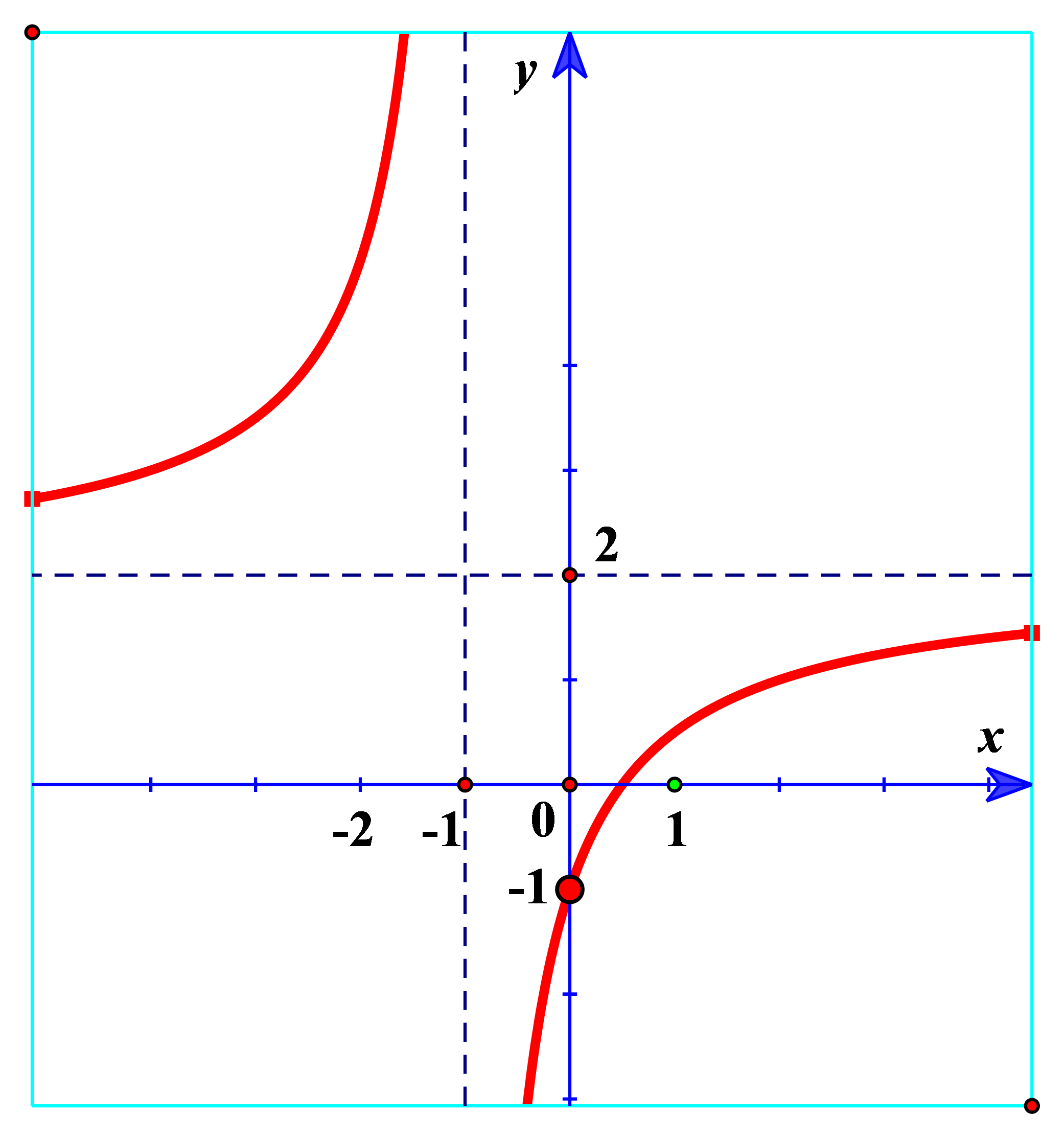
Dựa vào đồ thị ta thấy đường tiệm cận đứng của đồ thị hàm số là \(x = - 1\) nên loại B và D.
Đồ thị cắt trục tung tại điểm có tọa độ \(\left( {0; - 1} \right)\) chọn C.
Câu 3
Lời giải
Chọn B
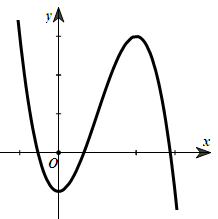
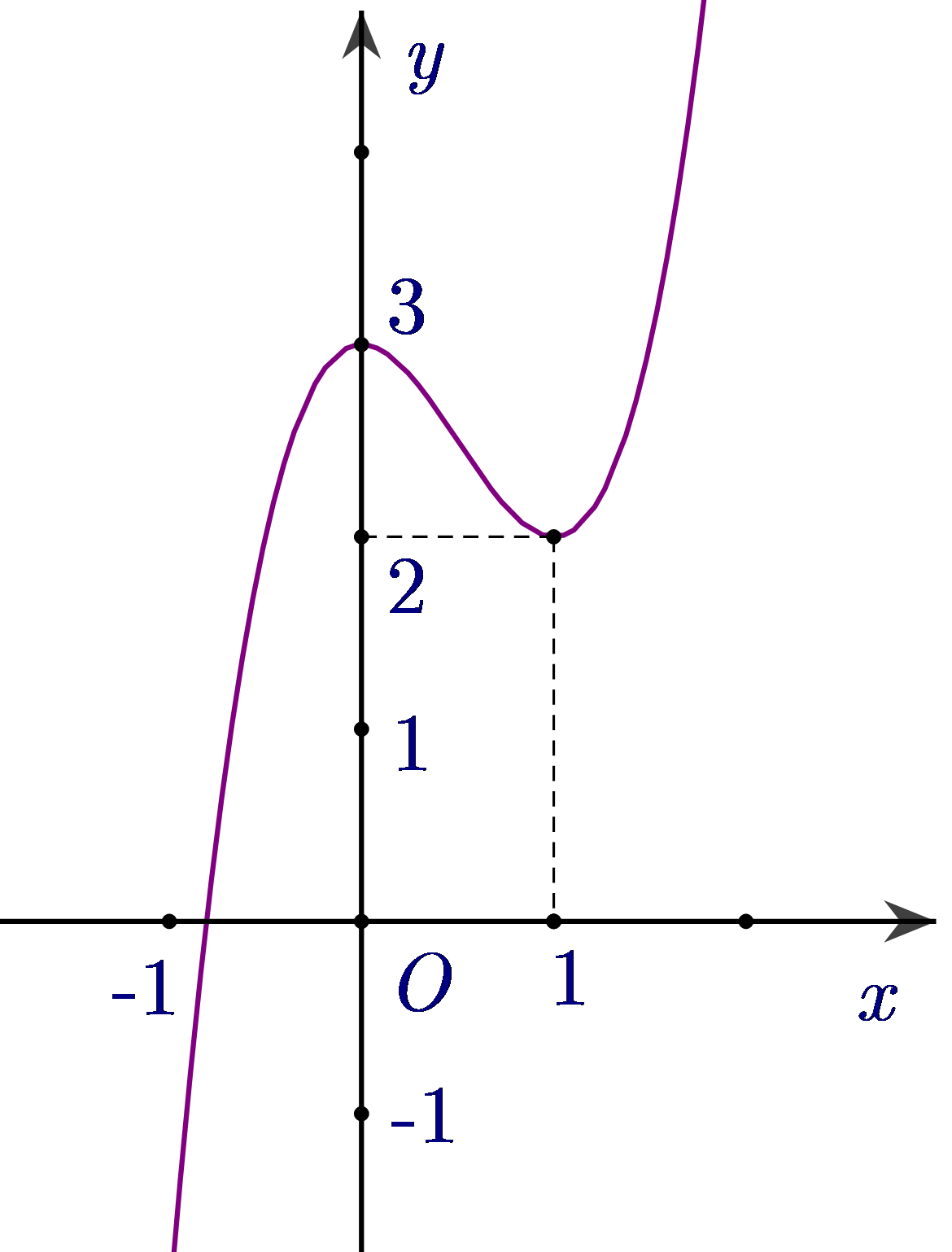
Dựa vào đồ thị ta thấy \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty \,\, \Rightarrow a < 0\)
Đồ thị hàm số cắt trục tung tại điểm \(\left( {0;d} \right)\,\, \Rightarrow \,d < 0\).
Câu 4
Lời giải
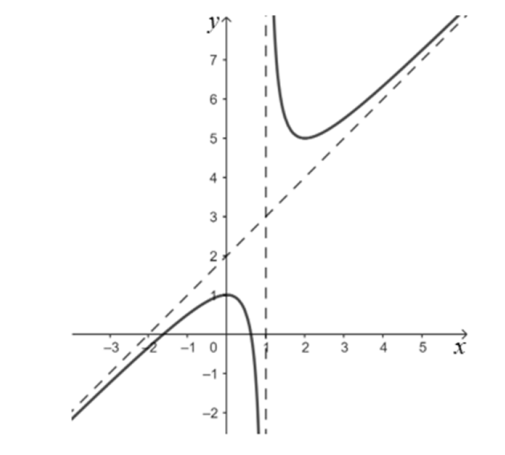
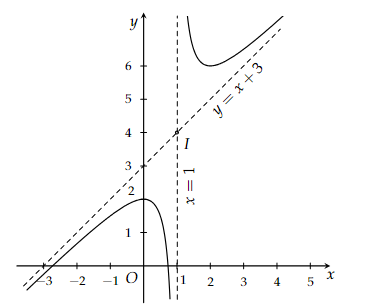
Dựa vào đồ thị ta thấy đường tiệm cận đứng của đồ thị hàm số là \(x = 1\) nên loại \(y = \frac{{{x^2} + x - 1}}{{x + 1}}\) và \(y = \frac{{{x^2} + x + 1}}{{x + 1}}\).
Đồ thị cắt trục tung tại điểm có tọa độ \(\left( {0;1} \right)\) chọn \(y = \frac{{{x^2} + x - 1}}{{x - 1}}\).
Câu 5
Lời giải
Chọn B
Đồ thị hàm số \(y = \frac{{3x + 2}}{{x - 1}}\) cắt trục hoành tại điểm có hoành độ \({x_0} = - \frac{2}{3}\)
Đồ thị hàm số \(y = \frac{{ - 2x + 4}}{{x - 1}}\) cắt trục hoành tại điểm có hoành độ \({x_0} = 2\)
Đồ thị hàm số \(y = \frac{{2x + 3}}{{x - 1}}\) cắt trục hoành tại điểm có hoành độ \({x_0} = - \frac{3}{2}\)
Đồ thị hàm số \(y = \frac{{2x + 1}}{{ - x + 1}}\) cắt trục hoành tại điểm có hoành độ \({x_0} = - \frac{1}{2}\).
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

![Tìm \[x\] để tam giác \[ABC\] có diện tích lớn nhất. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/10-1759202928.png)
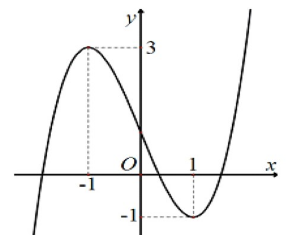
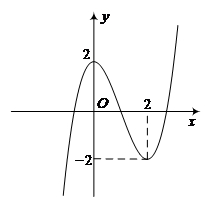
![Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị là đường cong trong hình sau. Phương trình \[f\left( {f\left( x \right)} \right) = 0\] có bao nhiêu nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/15-1759203193.png)