Đề thi minh họa (Dự thảo) TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Thanh Hóa
36 người thi tuần này 4.6 1.2 K lượt thi 18 câu hỏi 60 phút
🔥 Đề thi HOT:
Đề minh họa thi vào lớp 10 môn Toán năm 2026 TP. Hồ Chí Minh
712 lượt thi
7 câu hỏi
Đề thi tuyển sinh vào lớp 10 Toán năm học 2023 - 2024 Sở GD&ĐT Hà Nội có đáp án
401 lượt thi
7 câu hỏi
123 bài tập Nón trụ cầu và hình khối có lời giải
4 K lượt thi
123 câu hỏi
63 bài tập Tỉ số lượng giác và ứng dụng có lời giải
1.6 K lượt thi
63 câu hỏi
52 bài tập Hệ Phương trình bậc nhất hai ẩn và giải hệ phương trình bậc nhất hai ẩn có lời giải
1.2 K lượt thi
52 câu hỏi
52 bài tập Hệ thức lượng trong tam giác có lời giải
1.8 K lượt thi
52 câu hỏi
Đề thi thử TS vào 10 (Tháng 1) năm học 2025 - 2026_Môn Toán_THCS Cầu Giấy_Quận Cầu Giấy
3.8 K lượt thi
13 câu hỏi
45 bài tập Phương trình quy về phương trình bậc nhất 2 ẩn và hệ phương trình bậc nhất 2 ẩn có lời giải
1.3 K lượt thi
45 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
A. \(x = 9\).
B. \(x = - 3\).
C. \(x = 3\).
D. \(x = - 9\).
Lời giải
Đáp án đúng là: C
Giải phương trình:
\(3x - 9 = 0\)
\(3x = 9\)
\[x = 3\].
Vậy phương trình đã cho có nghiệm là \(x = 3\).
Câu 2
A. \(\sqrt {2{x^2}} \).
B. \(2\sqrt {{x^3}} \).
C. \(\sqrt {2{x^3}} \).
D. \( - 2\sqrt {{x^3}} \).
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
Với \(x \ge 0,\) ta có: \(2x\sqrt x = 2\sqrt {{x^2} \cdot x} = 2\sqrt {{x^3}} .\)
Câu 3
A. \(y = {x^2}\).
B. \(y = \frac{1}{2}{x^2}\).
C. \(y = 3{x^2}\).
D. \(y = \frac{1}{3}{x^2}\).
Lời giải
Đáp án đúng là: D
⦁ Thay \(x = 3\) vào hàm số \(y = {x^2},\) ta được: \[y = {3^2} = 9 \ne 3.\] Do đó đồ thị hàm số \(y = {x^2}\) không đi qua điểm \(\left( {3;3} \right).\)
⦁ Thay \(x = 3\) vào hàm số \(y = \frac{1}{2}{x^2},\) ta được: \[y = \frac{1}{2} \cdot {3^2} = \frac{9}{2} \ne 3.\] Do đó đồ thị hàm số \(y = \frac{1}{2}{x^2}\) không đi qua điểm \(\left( {3;3} \right).\)
⦁ Thay \(x = 3\) vào hàm số \(y = 3{x^2},\) ta được: \[y = 3 \cdot {3^2} = 27 \ne 3.\] Do đó đồ thị hàm số \(y = 3{x^2}\) không đi qua điểm \(\left( {3;3} \right).\)
⦁ Thay \(x = 3\) vào hàm số \(y = \frac{1}{3}{x^2},\) ta được: \[y = \frac{1}{3} \cdot {3^2} = 3.\] Do đó đồ thị hàm số \(y = \frac{1}{3}{x^2}\) đi qua điểm \(\left( {3;3} \right).\)
Vậy ta chọn phương án D.
Câu 4
A. \(x < 3\).
B. \(x > 3\).
C. \(x \le 3\).
D. \(x \ge 3\).
Lời giải
Đáp án đúng là: C
Giải bất phương trình:
\(2x + 3 \le 9\)
\(2x \le 6\)
\(x \le 3.\)
Vậy bất phương trình đã cho có nghiệm \(x \le 3.\)
Câu 5
A. \(\tan B = \frac{4}{3}\).
B. \(\tan C = \frac{4}{3}\).
C. \(\cot B = \frac{4}{3}\).
D. \(\cot C = \frac{3}{4}\).
Lời giải
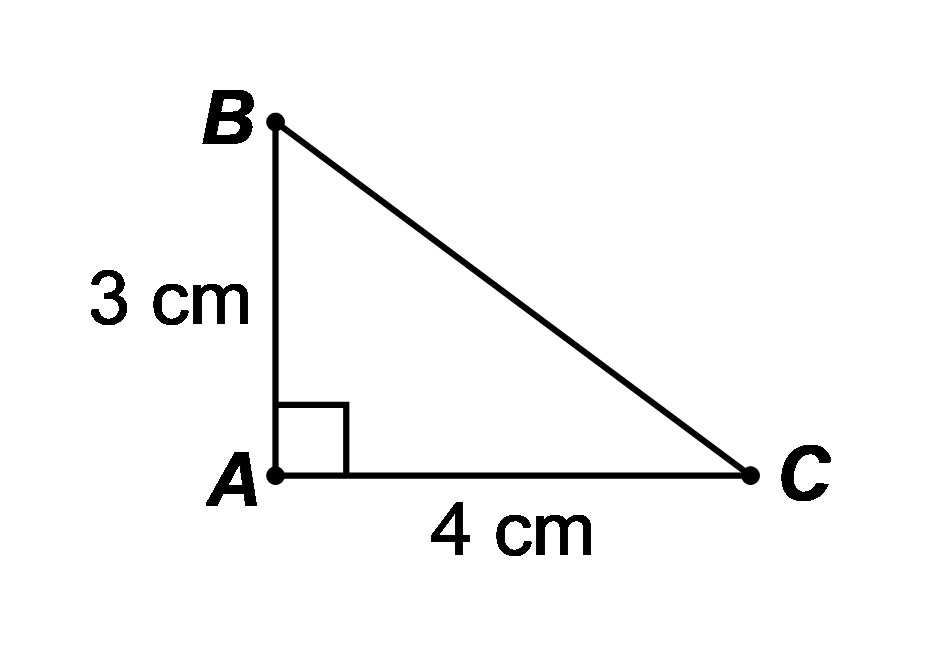
Đáp án đúng là: A
Xét \(\Delta ABC\) vuông tại \(A,\) ta có:
\(\tan B = \cot C = \frac{{AC}}{{AB}} = \frac{4}{3};\,\,\tan C = \cot B = \frac{{AB}}{{AC}} = \frac{3}{4}.\)Câu 6
A. 13 cm.
B. \(\frac{{13}}{2}\;{\rm{cm}}\).
C. \(\frac{{13\sqrt 2 }}{2}\;{\rm{cm}}\).
D. \(\frac{{5\sqrt 2 }}{2}\;{\rm{cm}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. \(\frac{3}{{10}}\).
B. \(\frac{4}{{10}}\).
C. \(\frac{7}{{10}}\).
D. \(\frac{3}{{14}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 1
II. PHẦN TỰ LUẬN (8,0 điểm)
Câu 9-10: (1,5 điểm)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 2
Câu 14-15: (1,0 điểm) Một quả cầu sắt \(\left( C \right)\) có dạng một khối cầu đặc có khối lượng riêng bằng \(7\,\,800\) kg/m3 và có khối lượng bằng \(1300\pi \) (kg). Biết công thức tính khối lượng của một vật là \(P = V \cdot D,\) trong đó \(P\) là khối lượng của vật (đơn vị kg), \[V\] là thể tích của vật (đơn vị m3) và \(D\) là khối lượng riêng của vật (đơn vị kg/m3).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Câu 16-17: (2,0 điểm) Cho tam giác \(ABC\) nhọn nội tiếp đường tròn \(\left( O \right)\) và các đường cao \(AD,\,\,BE\) của tam giác \(ABC\) cắt nhau tại \(H.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập