10 Bài tập Viết phương trình đường thẳng liên quan đến góc (có lời giải)

30 người thi tuần này 4.6 313 lượt thi 10 câu hỏi 45 phút

Câu 1

Trong mặt phẳng tọa độ Oxy, phương trình đường thẳng d có hệ số góc là số âm và đi qua A(–2; 0) tạo với đường thẳng Δ: x + 3y – 3 = 0 một góc 45° là

A. 2x + y + 4 = 0;

B. x + 2y + 4 = 0;

C. x – 2y – 2 = 0;

D. 2x + y – 4 = 0.

Lời giải

Hướng dẫn giải:

Đáp án đúng là: A

Gọi ${\vec{n}}_{d} (a; b)$ là vectơ pháp tuyến của đường thẳng d (với a² + b²≠ 0).

Đường thẳng d đi qua A(–2; 0) và có một vectơ pháp tuyến ${\vec{n}}_{d} (a; b)$ nên có phương trình là: a(x + 2) + b(y – 0) = 0 tức là ax + by + 2a = 0.

Đường thẳng Δ: x + 3y – 3 = 0 có một vectơ pháp tuyến ${\vec{n}}_{Δ} (1; 3) .$

Theo giả thiết d tạo với Δ một góc 45° nên:

$\cos (d, Δ) = \cos 45 ° \Leftrightarrow \frac{|a + 3 b|}{\sqrt{a^{2} + b^{2}} \cdot \sqrt{1^{2} + 3^{2}}} = \frac{\sqrt{2}}{2}$

$\Leftrightarrow 2 |a + 3 b| = \sqrt{20} \cdot \sqrt{a^{2} + b^{2}}$

$\Leftrightarrow 5 (a^{2} + b^{2}) = {(a + 3 b)}^{2} \Leftrightarrow 2 a^{2} - 3 a b - 2 b^{2} = 0 \Leftrightarrow [\begin{array}{l} a = 2 b \\ a = - \frac{1}{2} b \end{array}$ .

Với a = 2b, chọn b = 1 suy ra a = 2, ta được đường thẳng cần tìm là 2x + y + 4 = 0.

Với $a = - \frac{1}{2} b$ , chọn b = –2 suy ra a = 1, ta được đường thẳng cần tìm là x – 2y + 2 = 0 (loại do hệ số góc dương).

Câu 2

Trong mặt phẳng tọa độ Oxy, có bao nhiêu đường thẳng d đi qua điểm A(2; 0) và tạo với trục hoành một góc 45°?

A. Có duy nhất;

B. 2;

C. Vô số;

D. Không tồn tại.

Lời giải

Hướng dẫn giải:

Đáp án đúng là: B

Gọi ${\vec{n}}_{d} (a; b)$ là vectơ pháp tuyến của đường thẳng d (với a² + b²≠ 0).

Đường thẳng đi qua điểm A(2; 0) và có ${\vec{n}}_{d} (a; b)$ là vectơ pháp tuyến nên có phương trình là: a(x – 2) + b(y – 0) = 0 hay ax + by – 2a = 0.

Trục hoành Ox có phương trình y = 0 có vectơ pháp tuyến là ${\vec{n}}_{d} (a; b)$

Đường thẳng d tạo với trục hoành một góc 45° nên ta có:

$\cos 45 ° = \frac{|a \cdot 0 + b \cdot 1|}{\sqrt{a^{2} + b^{2}} \cdot \sqrt{0^{2} + 1^{2}}} \Leftrightarrow \frac{\sqrt{2}}{2} = \frac{|b|}{\sqrt{a^{2} + b^{2}}}$

⇔ 2(a² + b²) = 4b²

⇔ a² – b² = 0

⇔ a = b hoặc a = –b.

Vậy có hai đường thẳng đi qua A(2; 0) và tạo với trục hoành một góc 45°.

Câu 3

Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 3x – 4y – 12 = 0. Phương trình các đường thẳng Δ đi qua điểm M(2; –1) và tạo với d một góc 45° là

A. 7x – y – 15 = 0; x + 7y + 5 = 0;

B. 7x + y – 15 = 0; x – 7y + 5 = 0;

C. 7x – y + 15 = 0; x + 7y – 5 = 0;

D. 7x + y + 15 = 0; x – 7y – 5 = 0.

Lời giải

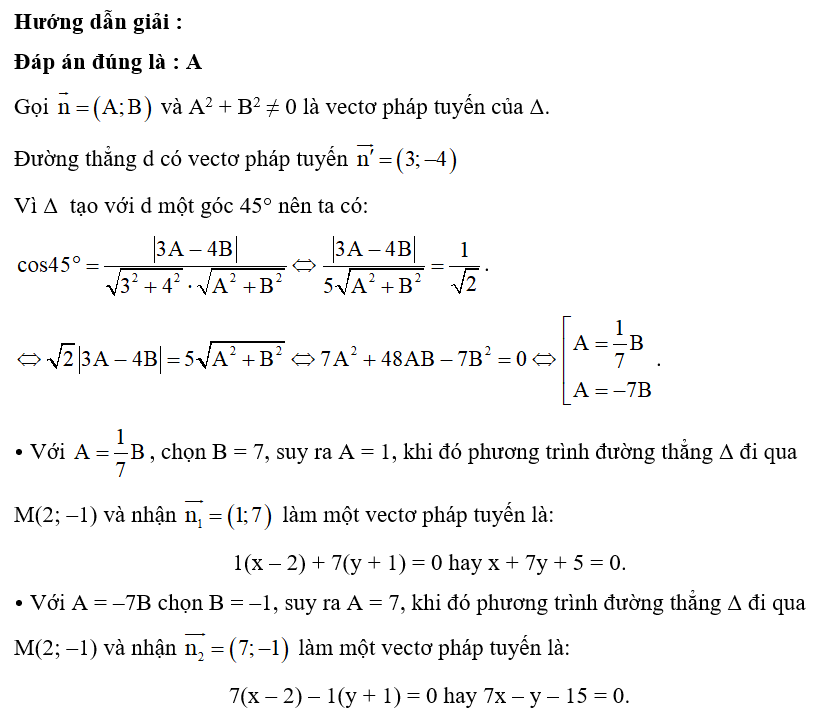
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 3x – 4y – 12 = 0. Phương trình các đường (ảnh 1)

Câu 4

Trong mặt phẳng tọa độ Oxy, phương trình đường thẳng d đi qua M(–1; 2) và tạo với trục Ox một góc 60° là

A. $\sqrt{3}$ x – y + $\sqrt{3}$ + 2 = 0;

B. $\sqrt{3}$ x – y – $\sqrt{3}$ + 2 = 0;

C. $\sqrt{3}$ x – y + 2 = 0

\sqrt{3}

x + y –

\sqrt{3}

+ 2 = 0.

Lời giải

Hướng dẫn giải:

Đáp án đúng là: A

Do d tạo với trục Ox một góc 60° nên có hệ số góc k = tan 60° = $\sqrt{3} \sqrt{3}$ .

Phương trình đường thẳng d là: y = $\sqrt{3}$ (x + 1) + 2

Hay $\sqrt{3}$ x – y + $\sqrt{3}$ + 2 = 0.

Câu 5

Trong mặt phẳng tọa độ Oxy, phương trình đường thẳng Δ đi qua M(1; 1) và tạo với đường thẳng d: x – y + 90 = 0 một góc 45° là

A. x – 1 = 0;

B. y – 1 = 0;

C. x + y – 2 = 0;

D. Cả A và B đúng.

Lời giải

Trong mặt phẳng tọa độ Oxy, phương trình đường thẳng Δ đi qua M(1; 1) và tạo với đường thẳng d: x – y + 90 = 0 một góc 45° là (ảnh 1)

Câu 6

Trong mặt phẳng tọa độ Oxy, đường thẳng Δ tạo với đường thẳng d: y = –2x + 4 một góc 45°. Hệ số góc k của đường thẳng Δ là

A. $k = \frac{1}{3}$ hoặc k = –3;

B. $k = \frac{1}{3}$ hoặc k = 3;

C. $k = - \frac{1}{3}$ hoặc k = –3;

k = - \frac{1}{3}

hoặc k = 3.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Biết rằng có đúng hai giá trị của tham số k để đường thẳng d: y = kx tạo với đường thẳng ∆: y = x một góc 60°. Tổng hai giá trị của k bằng

A. –8;

B. –4;

C. –1;

D. 1.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8

Đường thẳng Δ đi qua giao điểm của hai đường thẳng d₁: 2x + y – 3 = 0 và d₂: x – 2y + 1 = 0 đồng thời tạo với đường thẳng d₃: y – 1 = 0 một góc 45° có phương trình là

A. x + $(1 - \sqrt{2}) y$ = 0 hoặc x – y – 1 = 0;

B. x + 2y = 0 hoặc x – 4y = 0;

C. x – y = 0 hoặc x + y – 2 = 0;

D. 2x + 1 = 0 hoặc y + 5 = 0.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9

Trong mặt phẳng tọa độ Oxy, hai đường thẳng có phương trình (d₁) : x – y – 1 = 0, (d₂): 2x + y – 5 = 0. Gọi A là giao điểm của hai đường thẳng trên. Biết rằng có hai đường thẳng (d) đi qua M(1; –1) cắt hai đường thẳng trên lần lượt tại hai điểm B, C sao cho ABC là tam giác có BC = 3AB có dạng: ax + y + b = 0 và cx + y + d = 0, giá trị của T = a + b + c + d là

A. T = 5;

B. T = 6;

C. T = 2;

D. T = 0.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10

Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác cân ABC có cạnh đáy BC: x – 3y – 1 = 0, cạnh bên AB: x – y – 5 = 0. Đường thẳng AC đi qua M(−4; 1). Giả sử toạ độ đỉnh C(m; n). Giá trị T = m + n là

A. $T = \frac{5}{9}$ .

B. $T = - 3$ .

C. $T = \frac{9}{5}$ .

D. $T = - \frac{9}{5}$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tiếng Anh

Công nghệ

Tin học

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Viên chức

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Global success

iLearn Smart World

Friends Global

Bright

Explore new worlds

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Toán

Vật lý

Hóa học