8 câu Trắc nghiệm Toán 10 Cánh diều Giải Tam Giác có đáp án (Phần 2) (Thông hiểu)
20 người thi tuần này 4.6 1.9 K lượt thi 8 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 3
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 2
Đề kiểm tra Ôn tập chương 9 (có lời giải) -Đề 1
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 3
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 2
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 1
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: C
Có S = BC.CA.sinC
Gọi S’ là diện tích tam giác khi tăng cạnh BC lên 3 lần đồng thời tăng cạnh CA lên 3 lần và giữ nguyên độ lớn góc C
Ta có: S’ = .3BC.3CA.sinC = 9 . BC.CA.sinC = 9S.
Câu 2
A. ;
Lời giải
Đáp án đúng là: C
Ta có: S = AB.AC.sinA sinA = = = .
Câu 3
Lời giải
Đáp án đúng là: C
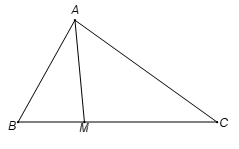
Câu 4
Lời giải
Đáp án đúng là: C

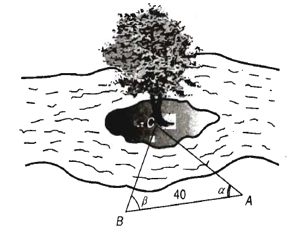
Câu 5
A. 53 m;
Lời giải
Đáp án đúng là: C
Từ định lí tổng ba góc trong tam giác ABC, suy ra .
Do đó, .
Áp dụng định lí sin vào tam giác ABC, ta có .
Suy ra AC = ≈ 41,47 (m) ≈ 41,5 (m).
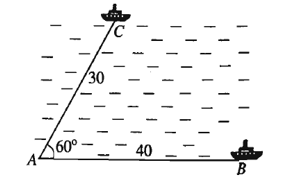
Câu 6
A. 61 hải lí;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. ;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.