5 câu Trắc nghiệm Toán 10 Cánh diều Tọa độ của vectơ (Phần 2) có đáp án (Vận dụng)
27 người thi tuần này 4.6 2 K lượt thi 5 câu hỏi 30 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 3
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 2
Đề kiểm tra Ôn tập chương 9 (có lời giải) -Đề 1
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 3
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 2
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 1
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Danh sách câu hỏi:
Câu 1
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Ta có \(\vec u = \vec v \Leftrightarrow \left\{ \begin{array}{l}{m^2} + 3 = 5m - 3\\2m = {m^2}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 5m + 6 = 0\\{m^2} - 2m = 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 3\\m = 2\end{array} \right.\\\left[ \begin{array}{l}m = 0\\m = 2\end{array} \right.\end{array} \right.\)
⇔ m = 2.
Suy ra m ∈ {2}.
Vậy ta chọn phương án A.
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
Gọi C(xC; yC).
Ta có: \(\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A}} \right) = \left( {3;9} \right)\) và \(\overrightarrow {BC} = \left( {{x_C} - {x_B};{y_C} - {y_B}} \right) = \left( {{x_C} - 7;{y_C} - 8} \right)\).
Ta có C là điểm đối xứng của A qua B.
Suy ra B là trung điểm của AC.
Do đó \(\overrightarrow {AB} = \overrightarrow {BC} \).
\( \Leftrightarrow \left\{ \begin{array}{l}3 = {x_C} - 7\\9 = {y_C} - 8\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 10\\{y_C} = 17\end{array} \right.\)
Suy ra tọa độ C(10; 17).
Vậy ta chọn phương án D.
Câu 3
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
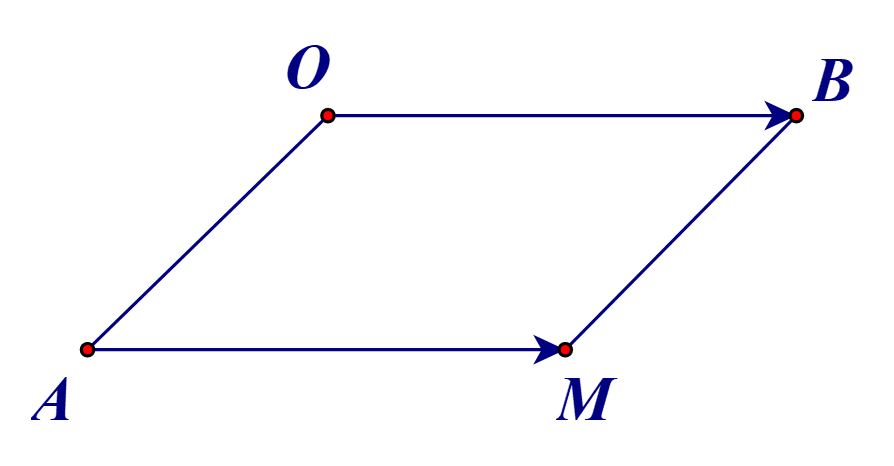
Ta có:
⦁ O(0; 0). Suy ra \(\overrightarrow {OB} = \left( {2;4} \right)\);
⦁ Gọi M(xM; yM). Suy ra \(\overrightarrow {AM} = \left( {{x_M} - 1;{y_M} + 1} \right)\).
Ta có tứ giác OBMA là hình bình hành.
\( \Leftrightarrow \overrightarrow {AM} = \overrightarrow {OB} \)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_M} - 1 = 2\\{y_M} + 1 = 4\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_M} = 3\\{y_M} = 3\end{array} \right.\)
Suy ra tọa độ M(3; 3).
Vậy ta chọn phương án C.
Câu 4
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
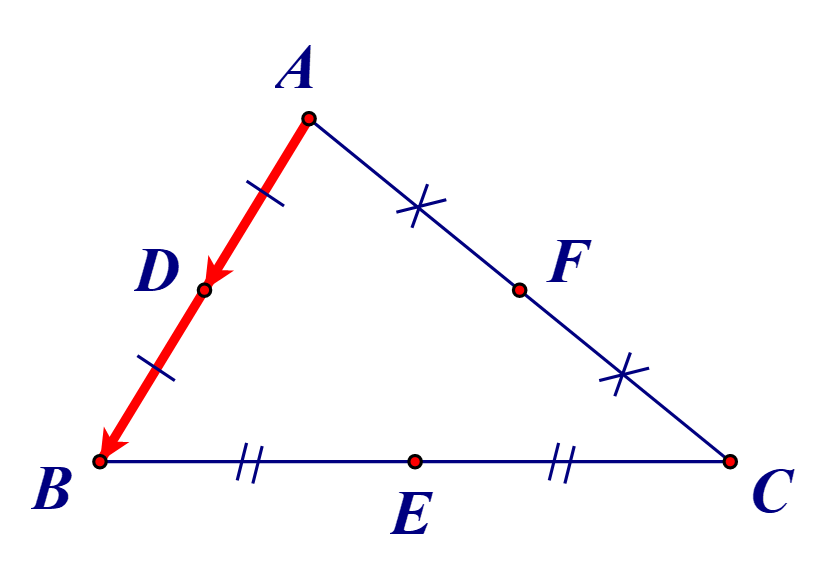
Gọi A(xA; yA), B(xB; yB), C(xC; yC).
Ta có: \(\overrightarrow {AD} = \left( {3 - {x_A};4 - {y_A}} \right)\) và \(\overrightarrow {DB} = \left( {{x_B} - 3;{y_B} - 4} \right)\).
Ta có D là trung điểm của AB.
Suy ra \(\overrightarrow {AD} = \overrightarrow {DB} \)
Khi đó \(\left\{ \begin{array}{l}3 - {x_A} = {x_B} - 3\\4 - {y_A} = {y_B} - 4\end{array} \right.\)
Vì vậy \(\left\{ \begin{array}{l}{x_A} + {x_B} = 6\,\,\,\,\left( 1 \right)\\{y_A} + {y_B} = 8\,\,\,\,\left( 2 \right)\end{array} \right.\)
Tương tự, ta được \(\left\{ \begin{array}{l}{x_B} + {x_C} = 12\,\,\,\,\left( 3 \right)\\{y_B} + {y_C} = 2\,\,\,\,\,\,\left( 4 \right)\end{array} \right.\) và \(\left\{ \begin{array}{l}{x_A} + {x_C} = 14\,\,\,\,\left( 5 \right)\\{y_A} + {y_C} = 6\,\,\,\,\,\,\left( 6 \right)\end{array} \right.\)
Từ (2), (4), (6), ta có hệ phương trình: \(\left\{ \begin{array}{l}{y_A} + {y_B} = 8\\{y_B} + {y_C} = 2\\{y_A} + {y_C} = 6\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{y_A} = 6\\{y_B} = 2\\{y_C} = 0\end{array} \right.\)
Vì vậy tổng tung độ ba đỉnh của tam giác ABC là: 6 + 2 + 0 = 8.
Do đó ta chọn phương án C.
Câu 5
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
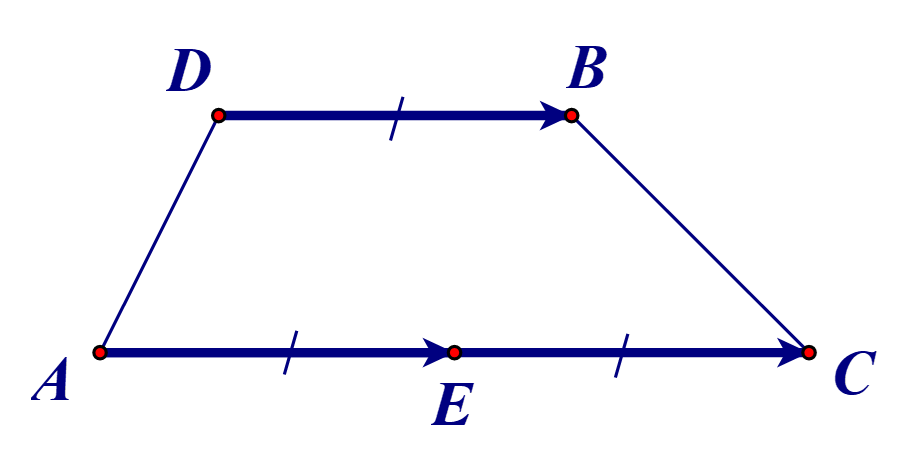
Gọi E(a; b) là trung điểm của AC.
Suy ra \(\overrightarrow {AE} = \overrightarrow {EC} \)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_E} - {x_A} = {x_C} - {x_E}\\{y_E} - {y_A} = {y_C} - {y_E}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_E} - 0 = - 6 - {x_E}\\{y_E} - \left( { - 1} \right) = 5 - {y_E}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}2{x_E} = - 6\\2{y_E} = 4\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_E} = - 3\\{y_E} = 2\end{array} \right.\)
Suy ra E(–3; 2).
Gọi D(xD; yD).
Ta có AE = \(\frac{1}{2}AC\) = DB.
Ta có AE // DB (giả thiết) và AE = DB (chứng minh trên).
Suy ra \(\overrightarrow {DB} = \overrightarrow {AE} \)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_B} - {x_D} = {x_E} - {x_A}\\{y_B} - {y_D} = {y_E} - {y_A}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}1 - {x_D} = - 3 - 0\\4 - {y_D} = 2 - \left( { - 1} \right)\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 4\\{y_D} = 1\end{array} \right.\)
Suy ra D(4; 1).
Vậy ta chọn phương án B.