Bộ 5 đề thi giữa kì 2 Toán 10 Kết nối tri thức cấu trúc mới có đáp án (Đề 5)
18 người thi tuần này 4.6 1.1 K lượt thi 20 câu hỏi 50 phút
🔥 Đề thi HOT:
13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)
16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án
60 câu Trắc nghiệm Toán 10 Bài hệ thức lượng trong tam giác có đáp án (Mới nhất)
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
Lời giải
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{2}{{x - 1}}\;{\rm{khi}}\;x \ge 2\\{x^2} + 1\;{\rm{khi}Đáp án đúng là: A
Có \(f\left( 2 \right) = \frac{2}{{2 - 1}} = 2;f\left( { - 2} \right) = {\left( { - 2} \right)^2} + 1 = 5\).
Do đó \(f\left( 2 \right) + f\left( { - 2} \right) = 7\).
Câu 2
Lời giải
Đáp án đúng là: B
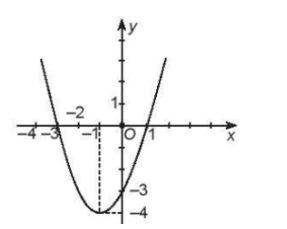
Trục đối xứng của \(\left( P \right)\) là đường thẳng có phương trình là \(x = - \frac{{ - 4}}{{2.\left( { - 3} \right)}} = - \frac{2}{3}\).
Câu 3
Lời giải
Đáp án đúng là: C
Để \(f\left( x \right) > 0,\forall x \in \mathbb{R}\)\( \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta < 0\end{array} \right.\).
Câu 4
Lời giải
Đáp án đúng là: C
Thay các nghiệm \(x\) vào phương trình ta thấy \(x = \frac{4}{3}\) là nghiệm.
Câu 5
Lời giải
Đáp án đúng là: D
Ta có \(\overrightarrow {AB} = \left( {1;4} \right)\).
Do đó một vectơ chỉ phương của đường thẳng \(AB\) là \(\overrightarrow {{u_4}} = \left( {1;4} \right)\).
Câu 6
A. \(d\left( {M,\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0}} \right|}}{{\sqrt {{a^2} + {b^2}} }}\).
B. \(d\left( {M,\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. \( - 4\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.