5 câu Trắc nghiệm Toán 10 Cánh diều Phương trình đường thẳng (Phần 2) có đáp án (Vận dụng)
31 người thi tuần này 4.6 1.7 K lượt thi 5 câu hỏi 30 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 3
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 2
Đề kiểm tra Ôn tập chương 9 (có lời giải) -Đề 1
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 3
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 2
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 1
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Danh sách câu hỏi:
Câu 1
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
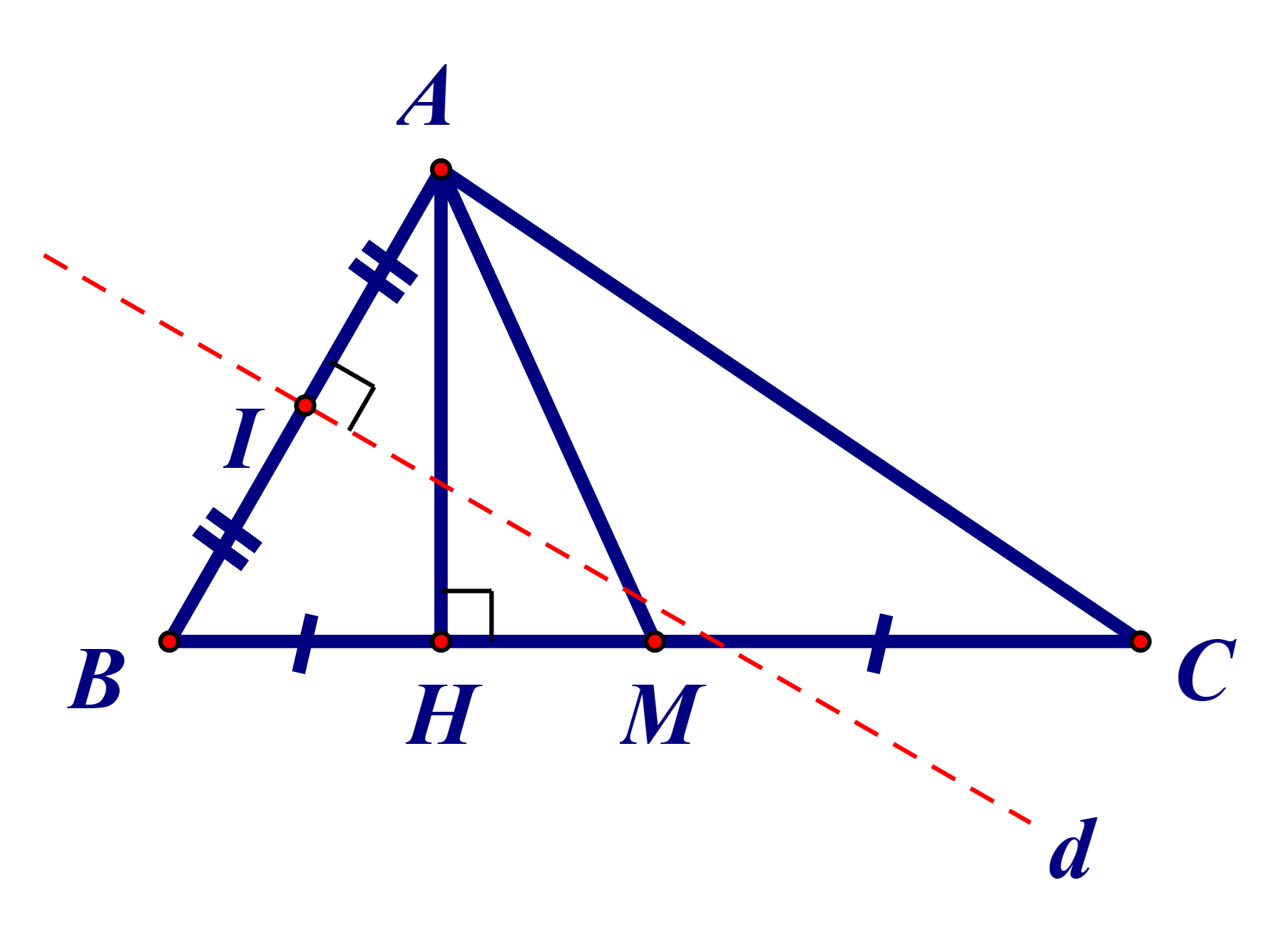
Ta có A ∈ AM.
Suy ra tọa độ A(1 + 3t; –2 – 7t).
Lại có A ∈ AH.
Suy ra 2(1 + 3t) + 5(–2 – 7t) + 66 = 0.
Do đó –29t + 58 = 0.
Vì vậy –29t = –58.
Khi đó t = 2.
Suy ra tọa độ A(7; –16).
Gọi I là trung điểm của cạnh AB.
Suy ra \(\left\{ \begin{array}{l}{x_I} = \frac{{{x_A} + {x_B}}}{2} = \frac{{7 + 4}}{2} = \frac{{11}}{2}\\{y_I} = \frac{{{y_A} + {y_B}}}{2} = \frac{{ - 16 - 3}}{2} = - \frac{{19}}{2}\end{array} \right.\)
Khi đó tọa độ \(I\left( {\frac{{11}}{2}; - \frac{{19}}{2}} \right)\).
Ta có \(\overrightarrow {AB} = \left( { - 3;13} \right)\).
Đường trung trực d của cạnh AB đi qua điểm \(I\left( {\frac{{11}}{2}; - \frac{{19}}{2}} \right)\) và có vectơ pháp tuyến \(\overrightarrow {AB} = \left( { - 3;13} \right)\).
Suy ra phương trình d: \( - 3\left( {x - \frac{{11}}{2}} \right) + 13\left( {y + \frac{{19}}{2}} \right) = 0\).
⇔ 3x – 13y – 140 = 0.
Vậy ta chọn phương án B.
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Chọn A(0; 1) ∈ ∆.
Đường thẳng ∆ có vectơ pháp tuyến \(\vec n = \left( {1;1} \right)\).
Suy ra đường thẳng ∆ nhận \(\vec u = \left( {1; - 1} \right)\) làm vectơ chỉ phương.
Đường thẳng ∆ đi qua A(0; 1) và có vectơ chỉ phương \(\vec u = \left( {1; - 1} \right)\).
Suy ra phương trình tham số của ∆: \(\left\{ \begin{array}{l}x = t\\y = 1 - t\end{array} \right.\)
Ta có M ∈ ∆. Suy ra M(t; 1 – t).
Ta có \(\overrightarrow {NM} = \left( {t + 1; - 2 - t} \right)\).
Suy ra \(NM = \left| {\overrightarrow {NM} } \right| = \sqrt {{{\left( {t + 1} \right)}^2} + {{\left( { - 2 - t} \right)}^2}} \).
Theo đề, ta có MN = 5.
⇔ (t + 1)2 + (–2 – t)2 = 25.
⇔ t2 + 2t + 1 + 4 + 4t + t2 = 25.
⇔ 2t2 + 6t – 20 = 0.
⇔ t = 2 hoặc t = –5.
Với t = 2, ta có tọa độ M(2; –1).
Với t = –5, ta có tọa độ M(–5; 6).
Vậy ta chọn phương án A.
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
Thế tọa độ điểm M(4; 5) vào phương trình ∆, ta được: \(\left\{ \begin{array}{l}4 = 2 - 3t\\5 = 1 + 2t\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}t = - \frac{2}{3}\\t = 2\end{array} \right.\)
Suy ra M(4; 5) ∉ ∆.
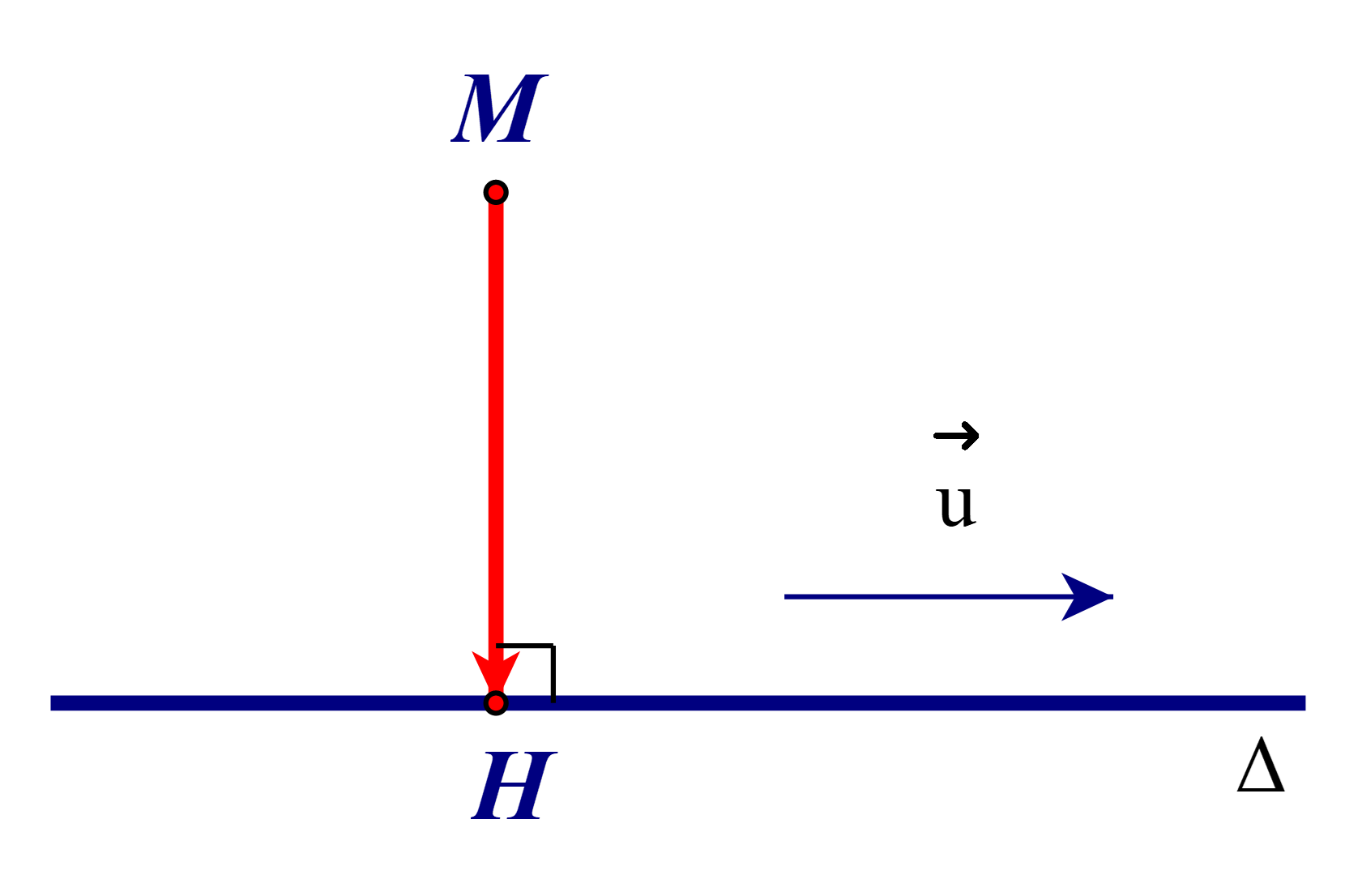
Gọi H là hình chiếu của M lên ∆.
Ta có H ∈ ∆. Suy ra tọa độ H(2 – 3t; 1 + 2t).
Ta có \(\overrightarrow {MH} = \left( { - 2 - 3t; - 4 + 2t} \right)\).
Đường thẳng ∆ có vectơ chỉ phương \(\vec u = \left( { - 3;2} \right)\).
Ta có \(\overrightarrow {MH} \bot \vec u\).
Suy ra \(\overrightarrow {MH} .\vec u = 0\).
Khi đó (–2 – 3t).(–3) + (–4 + 2t).2 = 0.
Vì vậy 13t – 2 = 0.
Suy ra \(t = \frac{2}{{13}}\).
Do đó tọa độ \(H\left( {\frac{{20}}{{13}};\frac{{17}}{{13}}} \right)\).
Vậy hoành độ hình chiếu H của điểm M lên đường thẳng ∆ là: \(\frac{{20}}{{13}} \approx 1,538\).
Vậy ta chọn phương án D.
Câu 4
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Ta có H ∈ d. Suy ra H(–5 + 2t; 9 – 5t).
Ta có:
⦁ \(\overrightarrow {HA} = \left( { - 2t + 3;5t - 8} \right)\);
⦁ \(\overrightarrow {HB} = \left( { - 2t + 8;5t - 4} \right)\). Suy ra \(2\overrightarrow {HB} = \left( { - 4t + 16;10t - 8} \right)\).
Suy ra \(\overrightarrow {HA} - 2\overrightarrow {HB} = \left( {2t - 13; - 5t} \right)\).
Ta có \(\left| {\overrightarrow {HA} - 2\overrightarrow {HB} } \right| = \sqrt {{{\left( {2t - 13} \right)}^2} + {{\left( { - 5t} \right)}^2}} = \sqrt {29{t^2} - 52t + 169} \)
\( = \sqrt {29\left[ {{{\left( {t - \frac{{26}}{{29}}} \right)}^2} + \frac{{4225}}{{841}}} \right]} \)
Ta có \({\left( {t - \frac{{26}}{{29}}} \right)^2} \ge 0,\,\,\forall t \in \mathbb{R}\)
\( \Leftrightarrow {\left( {t - \frac{{26}}{{29}}} \right)^2} + \frac{{4225}}{{841}} \ge \frac{{4225}}{{841}},\,\,\forall t \in \mathbb{R}\)
\( \Leftrightarrow 29\left[ {{{\left( {t - \frac{{26}}{{29}}} \right)}^2} + \frac{{4225}}{{841}}} \right] \ge 29.\frac{{4225}}{{841}} = \frac{{4225}}{{29}},\,\,\forall t \in \mathbb{R}\)
\[ \Leftrightarrow \sqrt {29\left[ {{{\left( {t - \frac{{26}}{{29}}} \right)}^2} + \frac{{4225}}{{841}}} \right]} \ge \sqrt {\frac{{4225}}{{29}}} = \frac{{65\sqrt {29} }}{{29}},\,\,\forall t \in \mathbb{R}\].
Dấu “=” xảy ra \( \Leftrightarrow t = \frac{{26}}{{29}}\).
Với \(t = \frac{{26}}{{29}}\), ta có \(H\left( { - \frac{{93}}{{29}};\frac{{131}}{{29}}} \right)\).
Khi đó \(\left| {\overrightarrow {HA} - 2\overrightarrow {HB} } \right|\) đạt giá trị nhỏ nhất bằng \[\frac{{65\sqrt {29} }}{{29}}\] khi \(H\left( { - \frac{{93}}{{29}};\frac{{131}}{{29}}} \right)\).
Vậy ta chọn phương án A.
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
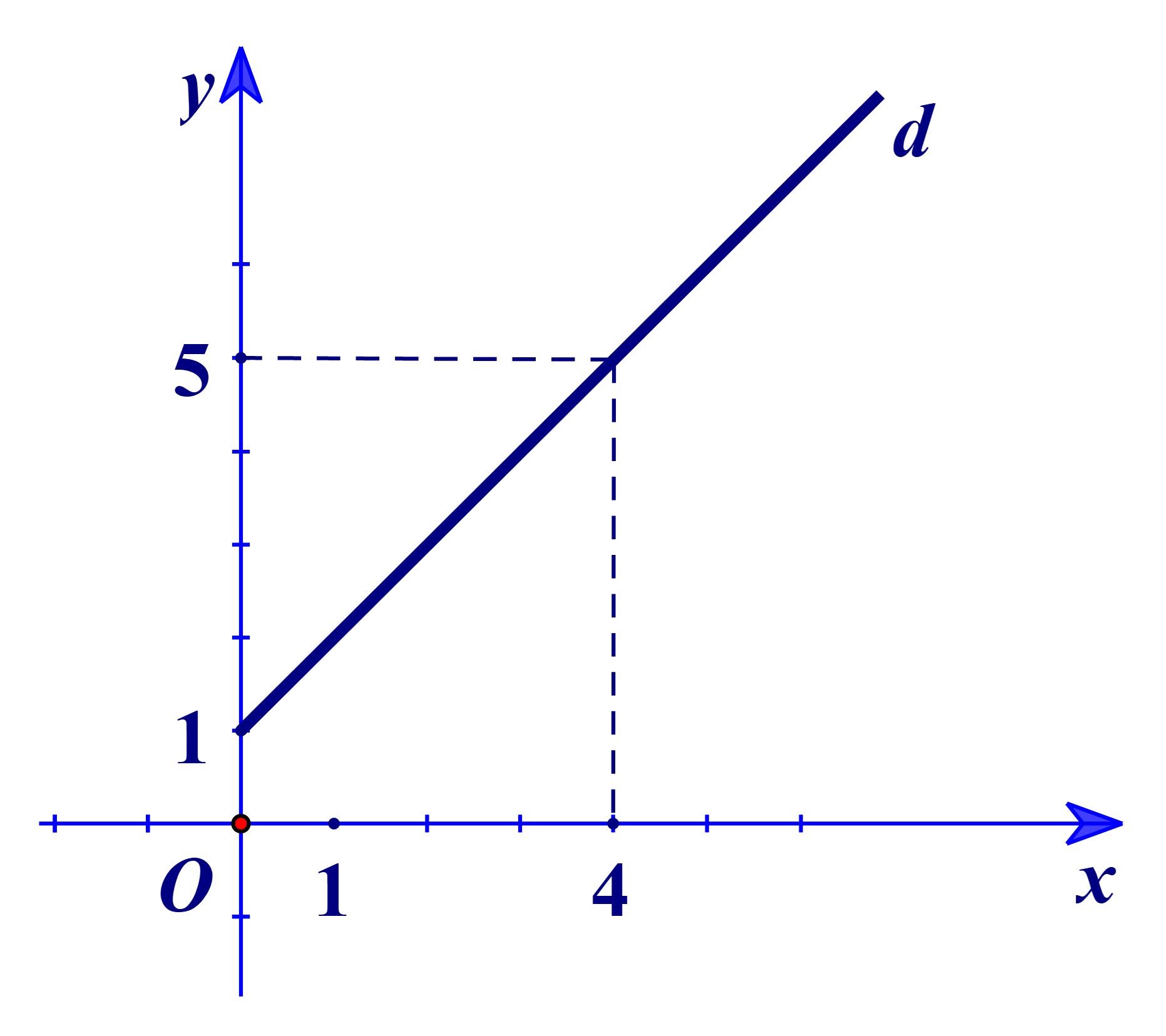
Quan sát hình vẽ, ta thấy đường thẳng d đi qua hai điểm có tọa độ (0; 1) và (4; 5).
Suy ra phương trình d: \(\frac{{x - 0}}{{4 - 0}} = \frac{{y - 1}}{{5 - 1}}\)
\( \Leftrightarrow \frac{x}{4} = \frac{{y - 1}}{4}\)
⇔ x = y – 1
⇔ y = x – 1.
Ta có: 15 giờ ứng với x = 15.
Với x = 15, ta có y = 15 – 1 = 14 (lít nước).
Vậy sau 15 giờ, bể nước chứa 14 lít nước.
Do đó ta chọn phương án A.