Đề kiểm tra Hai mặt phẳng song song (có lời giải) - Đề 2

Lời giải

Chọn D

Nếu mặt phẳng \(\left( P \right)\) có chứa hai đường thẳng phân biệt và hai đường thẳng đó cùng song song song với mặt phẳng \(\left( Q \right)\) thì mặt phẳng \(\left( P \right)\) song song với mặt phẳng \(\left( Q \right)\) là mệnh đề sai khi hai đường thẳng đó song song với nhau.

Chọn A

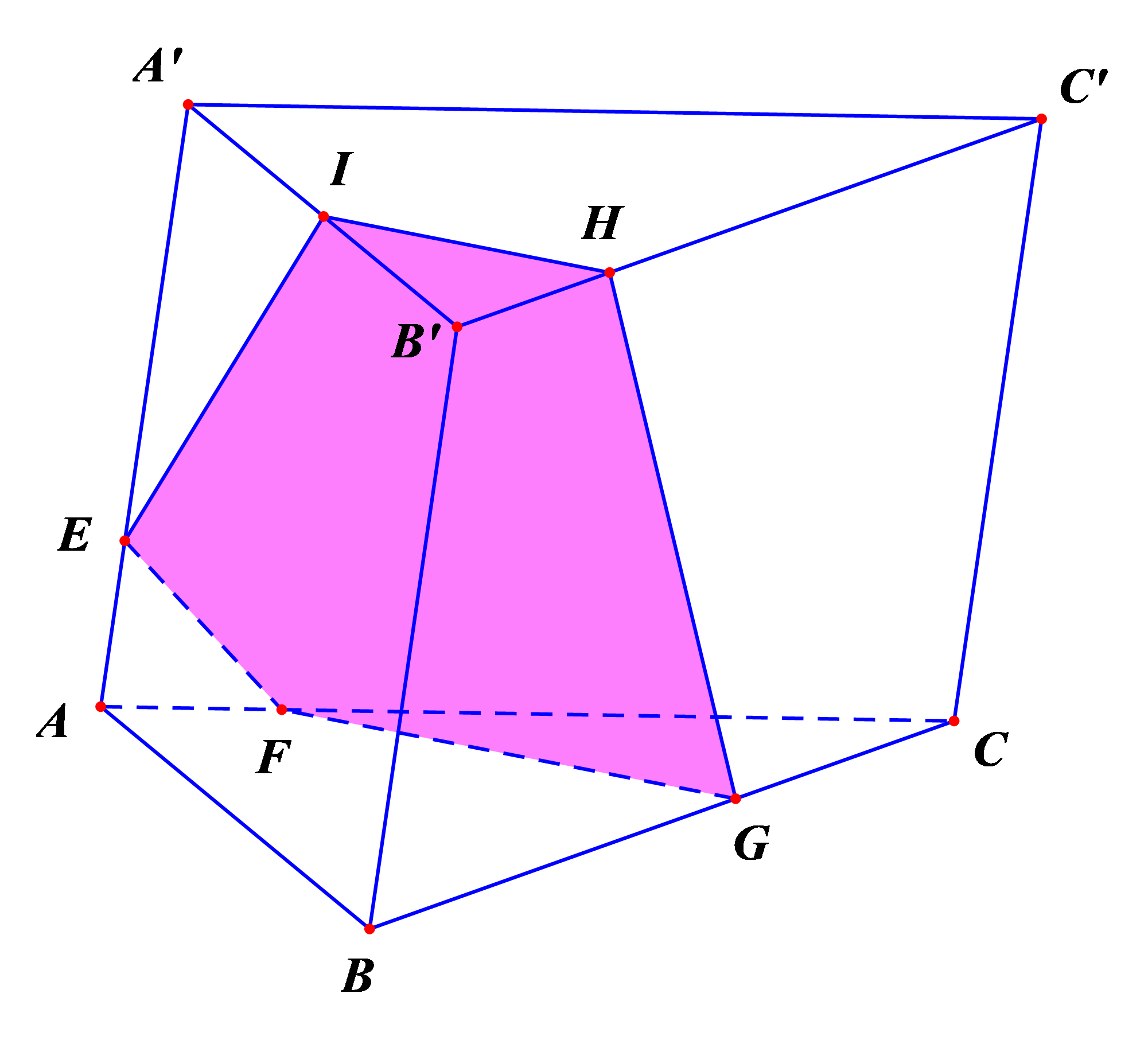
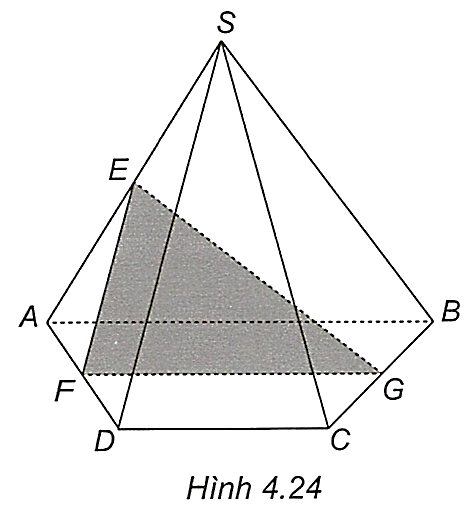
Một hình lăng trụ \(ABC.A'B'C'\) có tất cả \(5\) mặt. Do đó một phẳng cắt hình lăng trụ \(ABC.A'B'C'\) theo một thiết diện là hình đa giác có nhiều nhất là \(5\) cạnh.

Qua cách dựng trực tiếp, ta thấy số cạnh lớn nhất của thiết diện thu được là \(5\)

Chọn A

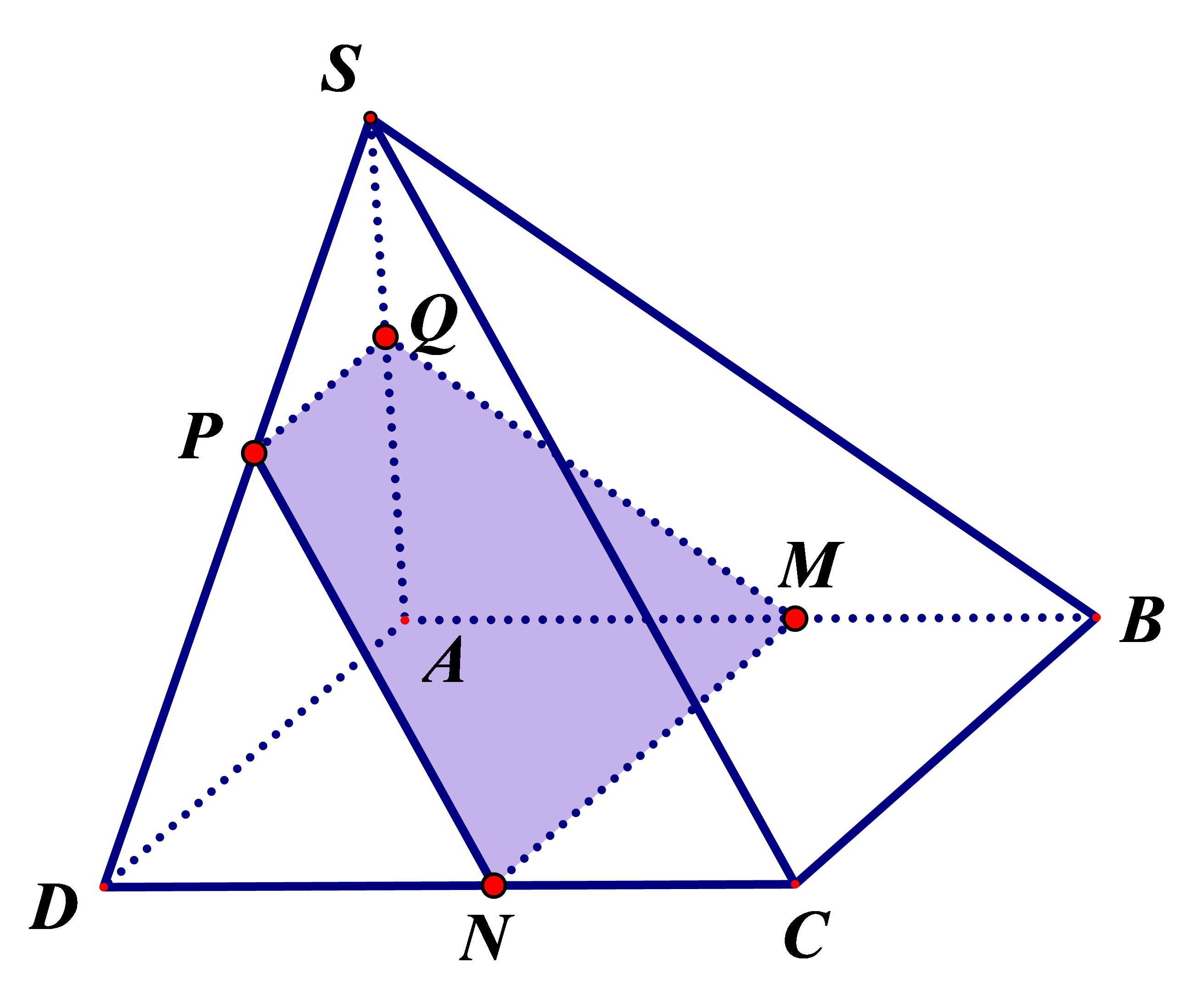
Do mặt phẳng \(\left( \alpha  \right)\) song song với \(\left( {SBC} \right)\) nên có:

giao tuyến của \(\left( \alpha  \right)\) và \(\left( {ABCD} \right)\) là đường chứa \(M\) và song song với \(BC\), cắt \(DC\) tại \(N\);

giao tuyến của \(\left( \alpha  \right)\) và \(\left( {SAB} \right)\) là đường chứa \(M\) và song song với \(SB\), cắt \(SA\) tại \(Q\);

giao tuyến của \(\left( \alpha  \right)\) và \(\left( {SCD} \right)\) là đường chứa \(N\) và song song với \(SC\), cắt \(SD\) tại \(P\);

do \(\left. \begin{array}{l}PQ = \left( \alpha  \right) \cap \left( {SAD} \right)\\\left( \alpha  \right) \supset MN\\\left( {SAD} \right) \supset AD\\MN//AD\end{array} \right\} \Rightarrow PQ//MN\).

Vậy thiết diện là hình thang \(MNPQ\).

Chọn A

Vẽ \(MN//CI\)và \(MP//SI\), khi đó thiết diện là tam giác \(MNP\).

Vì \(SABC\)là tứ diện đều nên \(SI = CI\) (các đường cao của tam giác đều). Mặt khác ta có \(\frac{{MP}}{{SI}} = \frac{{AP}}{{SA}} = \frac{{NP}}{{SC}} = \frac{{MN}}{{CI}}\).

Suy ra \(MP = MN \ne NP\) (do \(SC \ne CI\)).

Chọn C

Vì \[\left( \alpha  \right)//\left( {C{\rm{IJ}}} \right) \Rightarrow \left\{ \begin{array}{l}\left( \alpha  \right)//CI\\\left( \alpha  \right)//SC\end{array} \right.\]

\[\left( \alpha  \right)//CI\]và \[CI \subset (ABC)\]\[ \Rightarrow \]\[(ABC) \cap \left( \alpha  \right) = MN//CI\left( {N \in AC} \right)\]

\[\left( \alpha  \right)//SC\] và \[SC \subset (SAC)\] \[ \Rightarrow (SAC) \cap \left( \alpha  \right) = NP//SC\left( {P \in SA} \right)\]

\[ \Rightarrow \]\[\left( \alpha  \right) \equiv \left( {MNP} \right)\]

Vậy thiết diện của mặt phẳng \[\left( \alpha  \right)\] và tứ diện là tam giác \[\Delta MNP\].

Ta có \[\left\{ \begin{array}{l}MN//IC\\PN//SC\end{array} \right. \Rightarrow \frac{{MN}}{{IC}} = \frac{{AM}}{{IC}} = \frac{{AN}}{{AC}} = \frac{{PN}}{{SC}} = \frac{{AP}}{{SA}} = k\]

\[ \Rightarrow \]\[MP//SI\]\[ \Rightarrow \]\[\frac{{MP}}{{SI}} = k\]

Do tứ diện đều nên \[\Delta SAB = \Delta ABC \Rightarrow SI = IC\]\[ \Leftrightarrow MP = MN\]

Vậy tam giác \[\Delta MNP\] cân tại \[M\].

Chọn B

Ta có \(\left( \alpha  \right){\rm{//}}\left( {SAB} \right) \Rightarrow \left\{ \begin{array}{l}\left( \alpha  \right){\rm{//}}AB\\\left( \alpha  \right){\rm{//}}SA\end{array} \right.\)

\(\left( \alpha  \right){\rm{//}}AB \Rightarrow \left( \alpha  \right) \cap \left( {ABCD} \right) = MK{\rm{//}}AB\left( {I \in MK} \right)\begin{array}{*{20}{c}}{}&{\left( 1 \right)}\end{array}\)

\(\left( \alpha  \right){\rm{//}}SA \Rightarrow \left( \alpha  \right) \cap \left( {SAD} \right) = MH{\rm{//}}SA\)

\(\left( \alpha  \right){\rm{//}}AB \Rightarrow \left( \alpha  \right){\rm{//}}CD \Rightarrow \left( \alpha  \right) \cap \left( {SCD} \right) = HN{\rm{//}}CD\begin{array}{*{20}{c}}{}&{\left( 2 \right)}\end{array}\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\)\( \Rightarrow MK{\rm{//}}HN\).

Vậy thiết diện của hình chóp với \(\left( \alpha  \right)\) đi qua \(I\) và song song với \(mp\left( {SAB} \right)\) là hình thang \(MHNK\).

Chọn B

Diện tích tam giác \[ABC\]là \[{S_{\Delta ABC}} = \frac{1}{2}.AB.AC.\sin \widehat {BAC} = \frac{1}{2}.2\sqrt 3 .2\sqrt 3 .\sin {30^0} = 3.\]

Gọi \[N,\,\,P\]lần lượt là giao điểm của mặt phẳng \[\left( P \right)\]và các cạnh \[\,SC\]và \(SB\).

Vì \[\left( P \right)\]//\[\left( {ABC} \right)\] nên theo định lí Talet, ta có \[\frac{{SM}}{{SA}} = \frac{{SN}}{{SC}} = \frac{{SP}}{{SB}} = \frac{2}{3}.\]

Khi đó \[\left( P \right)\]cắt hình chóp \[S.ABC\]theo thiết diện là tam giác \[MNP\]đồng dạng với tam giác \[ABC\]theo tỉ số \[k = \frac{2}{3}.\]Vậy \[{S_{\Delta MNP}} = {k^2}.{S_{\Delta ABC}} = {\left( {\frac{2}{3}} \right)^2}.3 = \frac{4}{3}.\]