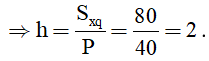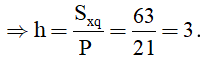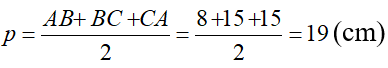Bài tập Diện tích xung quanh của hình lăng trụ đứng (có lời giải chi tiết)

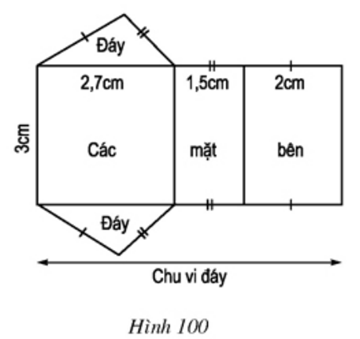
- Độ dài các cạnh của hai đáy là: 2,7 cm; 1,5 cm; 2 cm

- Diện tích của mỗi hình chữ nhật là: 3. 2,7 = 8,1(cm2); 3. 1,5 = 4,5(cm2); 3.2 = 6(cm2)

- Tổng diện tích của cả ba hình chữ nhật là: 8,1 + 4,5 + 6 = 18, 6 (cm2)

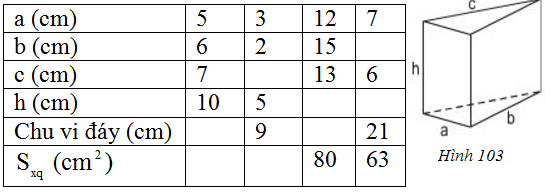
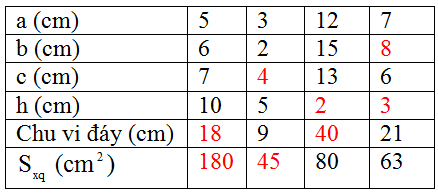
Dựa vào công thức: Sxq = 2p.h với p là nửa chu vi, h là chiều cao để điền các số vào bảng:

+ Chu vi đáy P = a + b + c (kí hiệu P là chu vi đáy)

+ Diện tích xung quanh = chu vi đáy x chiều cao

Ta có:

+ Cột 1: a = 5; b = 6; c = 7

P = a + b + c = 5 + 6 + 7 = 18

Sxq = Ph = 18.10 = 180.

+ Cột 2: a = 3; b = 2; P = 9

c = P - a - b = 9 - 3 - 2 = 4

Sxq = Ph = 9.5 = 45

+ Cột 3: a = 12; b = 15; c = 13

P = a + b + c = 12 + 15 + 13 = 40

+ Cột 4: a = 7; c = 6; P = 21

b = P - a - c = 21 - 7 - 6 = 8

Ta có bảng hoàn chỉnh sau:

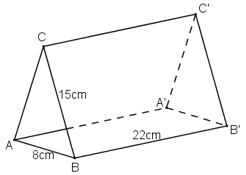
a)

Cạnh AC song song với cạnh A'C'.

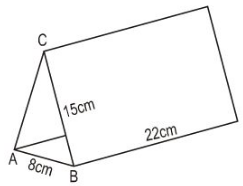
b) Do tam giác ABC cân tại C nên AC = BC = 15 cm.

Nửa chu vi tam giác đáy là:

Diện tích miếng bìa dùng để làm tấm lịch như trên là diện tích xung quanh của lăng trụ đứng:

Sxq = 2p.h =2.19.22= 836 (cm2)

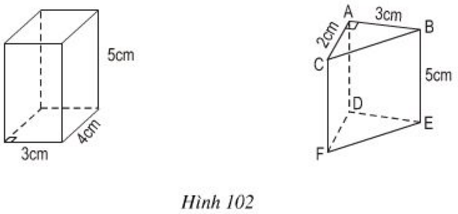
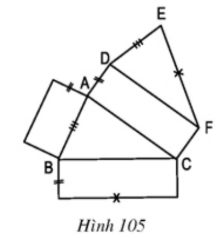
a) Từ hình khai triển bên, ta có thể gấp theo các cạnh để được hình lăng trụ đứng.

b) Các phát biểu đúng:

- Cạnh AD vuông góc với cạnh AB.

- EF và CF là hai cạnh vuông góc với nhau.

- Hai đáy (ABC) và (DEF) nằm trên hai mặt phẳng song song với nhau.