Dạng 1: Phiếu luyện tập số 1 có đáp án

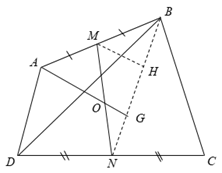
Gọi O là giao điểm của AG và MN

Gọi H là trung điểm của BG

Theo tính chất của trọng tâm, ta có: BH = HG = GN

Xét $\Delta ABG$ có MH là đường trung bình => MH // AG

Xét $\Delta HMN$ có AG // MH và NG = GH nên ON = OM

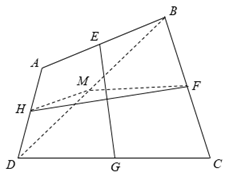
Gọi M là trung điểm của BD

Xét $\Delta ABD$ có HM là đường trung bình nên $HM=\frac{AB}{2}$

Xét $\Delta BDC$ có MF là đường trung bình nên $MF=\frac{CD}{2}$

Xét ba điểm M, H, F có $HF\le MH+MF=\frac{AB+CD}{2}$

Chứng minh tương tự, ta được: $EG\le \frac{AD+BC}{2}$.

Vậy  $HF+EG\le \frac{AB+CD+AB+CD}{2}=\frac{4a}{2}=2a$

Suy ra một trong hai đoạn HF, EG có độ dài không lớn hơn a.

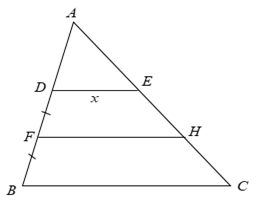
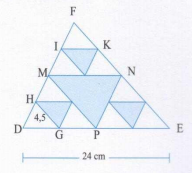
Gọi F là trung điểm của DB. Khi đó: AD = DF = FB

Vẽ $FH//BC\left(H\in AC\right)$

Xét $\Delta AFH$ có DE // FH và AD = DF nên AE = EH

Xét hình thang DECB có FH // BC và DF = FB nên EH = HC

Ta đặt DE = x

Ta có DE là đường trung bình của $\Delta AFH\Rightarrow DF=\frac{1}{2}FH$ => FH = 2x

Ta có FH là đường trung bình của hình thang DECB $\Rightarrow FH=\frac{DE+BC}{2}\Rightarrow 2x=\frac{x+6}{2}\Rightarrow x=2\left(cm\right)$

Vậy DE = 2 (cm).

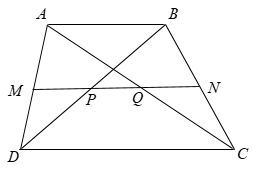
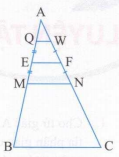
a) Xét $\Delta ABD$có MP là đường trung bình $\Rightarrow MP//AB\Rightarrow MP//CD$

Xét $\Delta ADC$ có MQ là đường trung bình => MQ // CD

Xét hình thang ABCD có MN là đường trung bình => MN // CD

Qua điểm M có các đường thẳng MP, MQ, MN cùng song song với CD nên các đường thẳng trùng nhau, suy ra bốn điểm M, N, P, Qthẳng hàng.

b) Ta có MN // CD nên PQ // CD; $PQ=MQ-MP=\frac{CD}{2}-\frac{AB}{2}=\frac{CD-AB}{2}$