Dạng 1. Vận dụng tính chất của hình bình hành để chứng minh các tính chất hình học có đáp án
26 người thi tuần này 4.6 2.5 K lượt thi 4 câu hỏi 45 phút
🔥 Đề thi HOT:
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
16.9 K lượt thi
18 câu hỏi
Đề kiểm tra Cuối kì 1 Toán 8 KNTT có đáp án (Đề 1)
13.2 K lượt thi
19 câu hỏi
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
6.3 K lượt thi
21 câu hỏi
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
4.8 K lượt thi
15 câu hỏi
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 2)
12.8 K lượt thi
17 câu hỏi
Đề kiểm tra Cuối kì 2 Toán 8 CTST có đáp án (Đề 1)
3.2 K lượt thi
18 câu hỏi
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
4.2 K lượt thi
10 câu hỏi
Dạng 1: Bài luyện tập 1 dạng 1: Tính có đáp án
4.8 K lượt thi
13 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
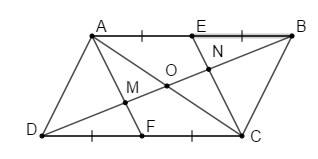
a) Ta có ABCD là hình bình hành nên
AB = CD (tc hbh).
Mà E, F là trung điểm cuả AB và CD
=> AB = CF = BE = DF .
Xét tứ giác AECF, có
AEFC là hình bình hành => AF // ECLời giải
b) Gọi
Xét có DO, AF là trung tuyến;
=> M là trọng tâm của
Xét có: BO, CE là trung tuyến,
=> N là trọng tâm của
Từ (2) và (4)
Từ (1); (3) và (5)
=> DM = BN = MN (đpcm).Lời giải
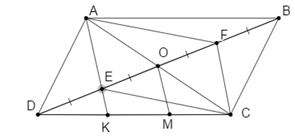
a)
E, F là trung điểm của DO và BO nên: DE = EO = OF = FB
Xét tứ giác AFCE, có:
=> AFCE là hình bình hành (dhnb)
=> AE // CF (tc hbh).Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
4.6
507 Đánh giá
50%
40%
0%
0%
0%