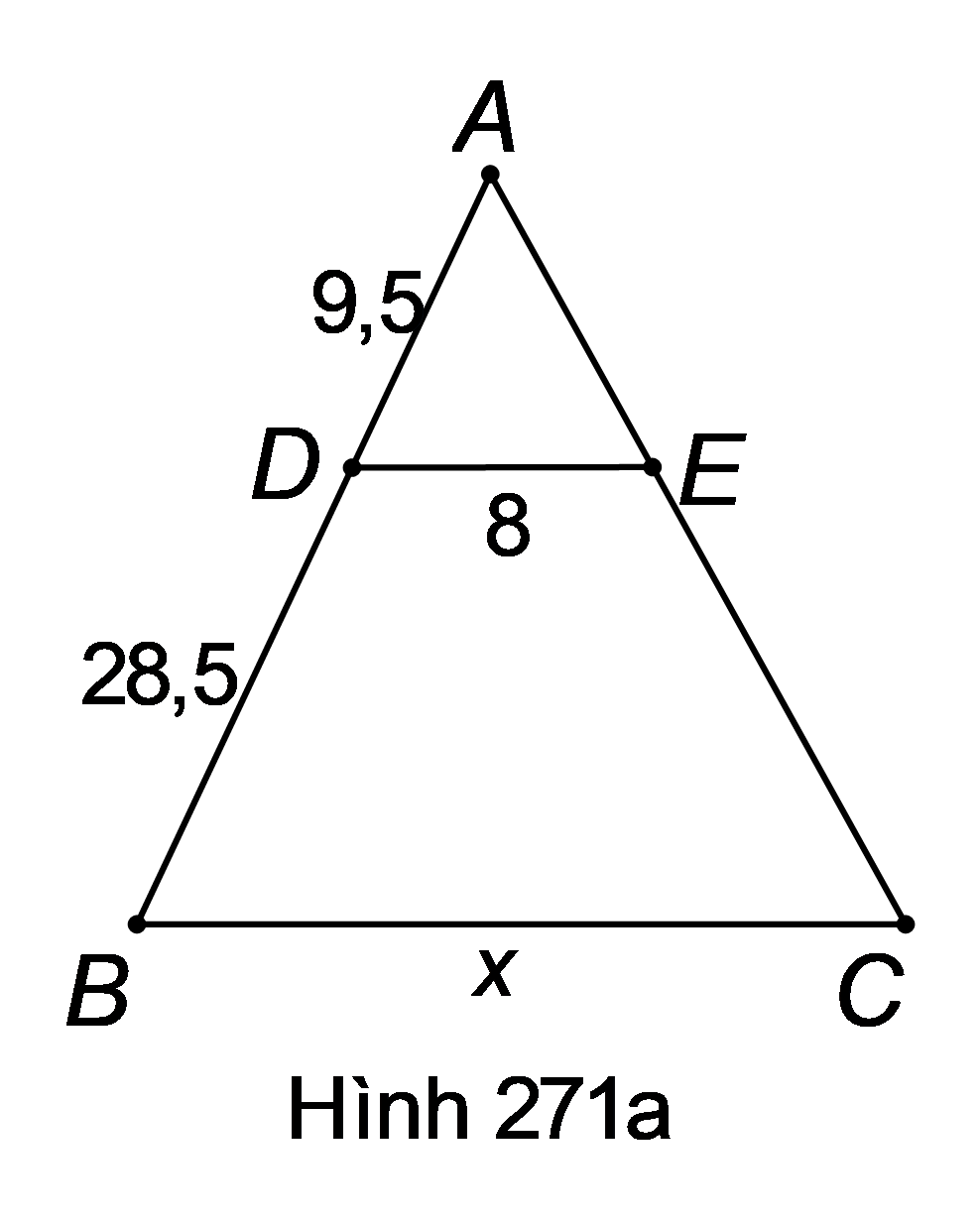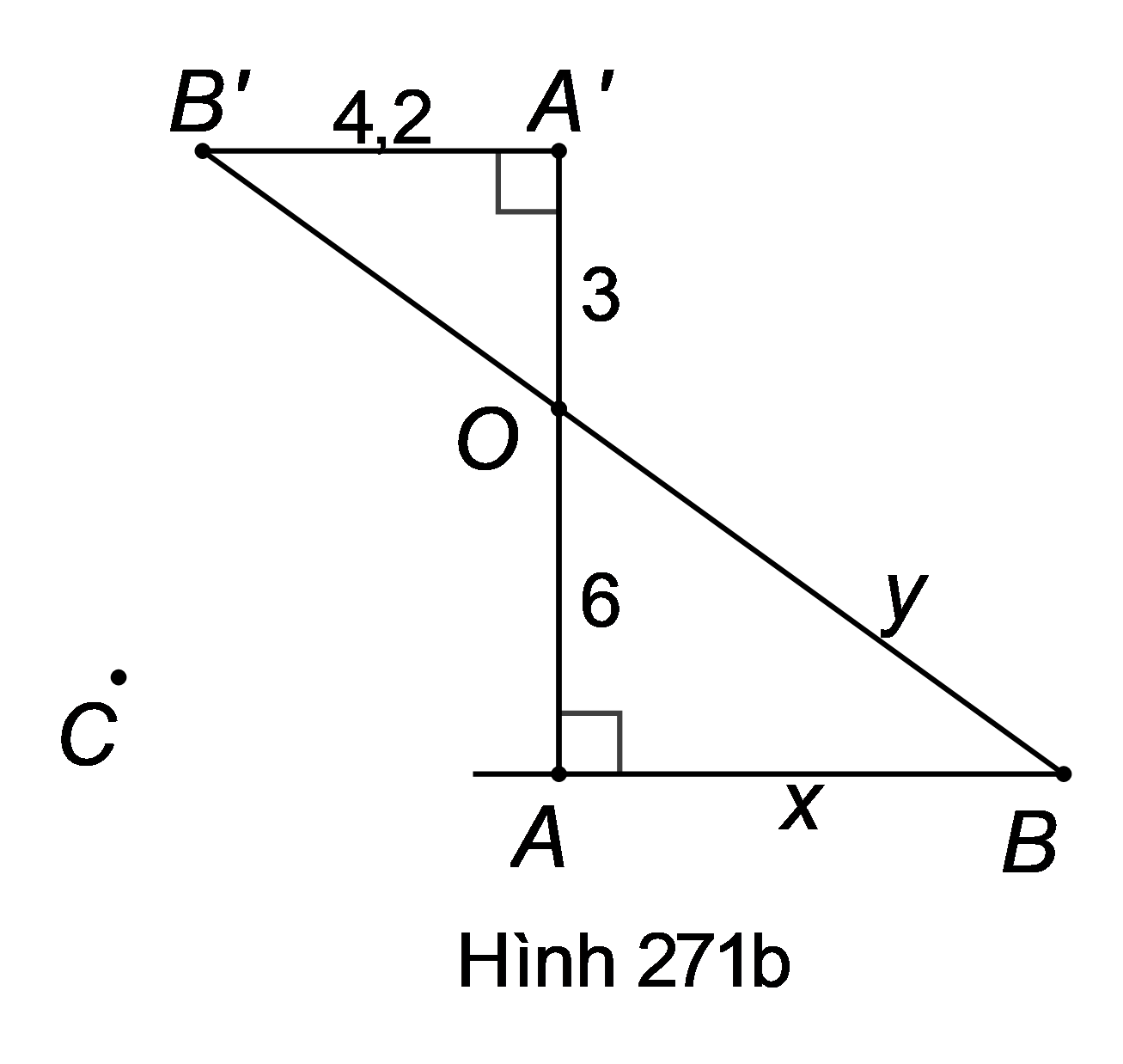Dạng 1. Tính độ dài đoạn thẳng. Chia đoạn thẳng cho trước thành các phần bằng nhau
71 người thi tuần này 4.6 3.7 K lượt thi 4 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 10
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 09
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 08
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 07
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 06
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 05
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 04
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 03
Danh sách câu hỏi:
Lời giải
Áp dụng hệ quả của định lí Ta-lét cho , ta được:
hay
.
Lời giải
Từ hình 271b ta thấy vì cùng vuông góc với .
Áp dụng hệ quả của định lí Ta-lét cho , ta được: hay .
Áp dụng định lí Py-ta-go vào tam giác OAB vuông ở A, ta được:
hay .
Lời giải
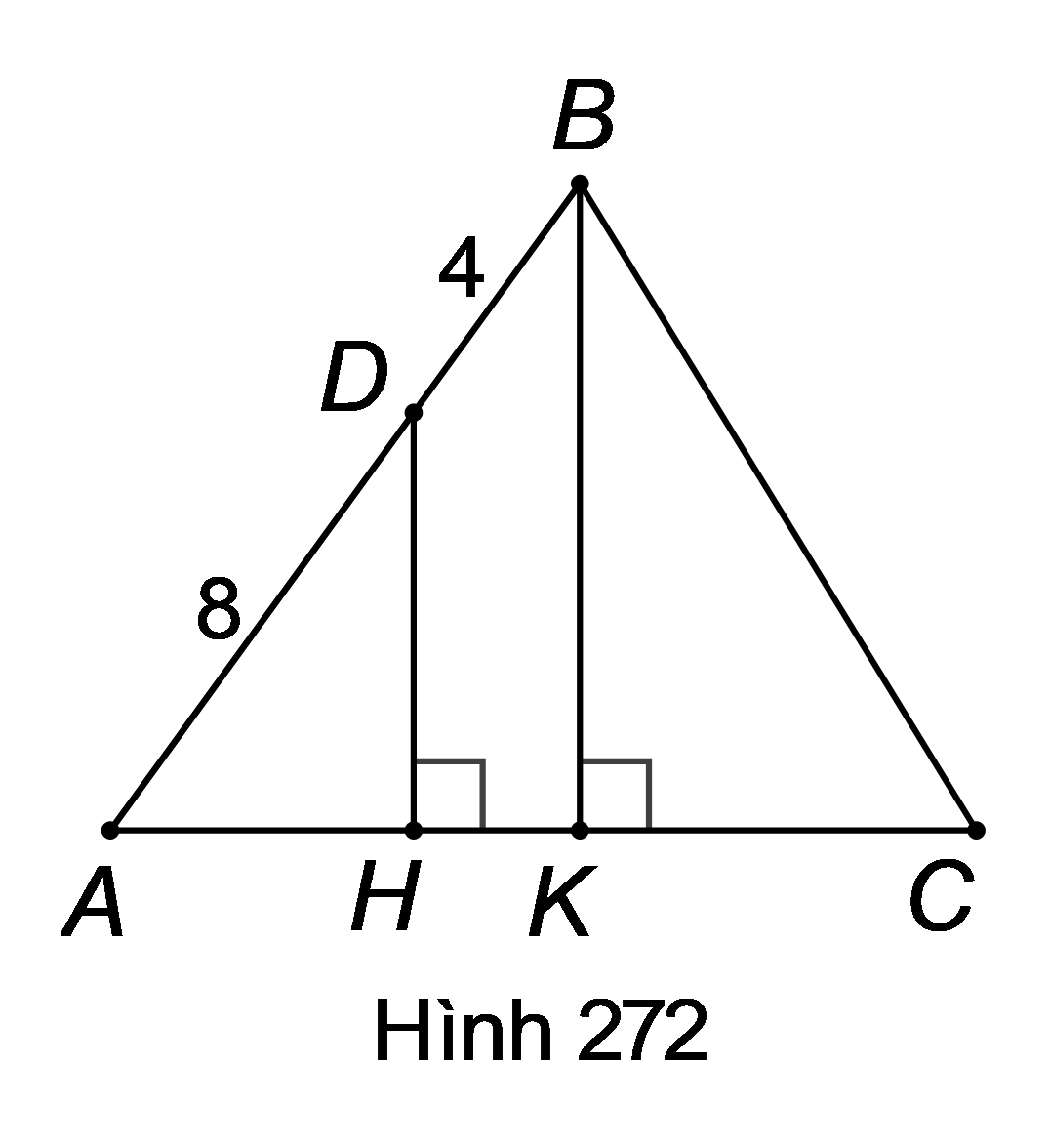
Kẻ DH và BK cùng vuông góc với AC thì và lần lượt là khoảng cách từ các điểm D và B đến cạnh AC.
Áp dụng hệ quả của định lí Ta-lét cho thu được hay .
Lời giải
Có hai cách chia một đoạn AB cho trước thành 5 phần bằng nhau.
Cách 1: Sử dụng hệ quả của định lí Ta-lét.
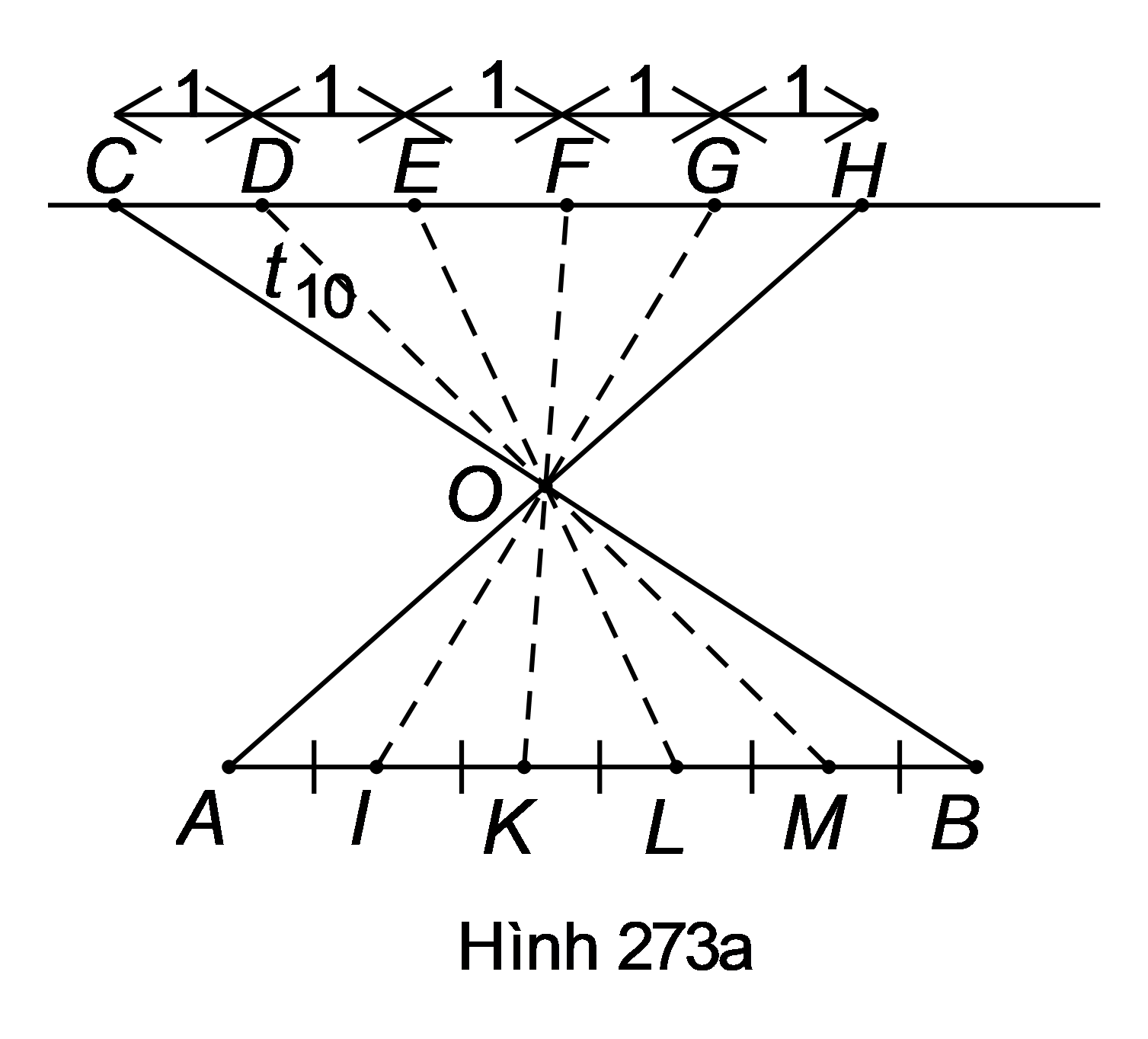
Kẻ đường thẳng .
Từ điểm C bất kì trên a, đặt liên tiếp các đoạn thẳng bằng nhau:
.
Gọi O là giao điểm của AH và BC.
Vẽ các đường thẳng cắt AB theo thứ tự ở thì các điểm này chia đoạn AB thành 5 phần bằng nhau. Thật vậy:
Áp dụng hệ quả của định lí Ta-lét cho , ta được:
do .
Chứng minh tương tự, ta được: .
Cách 2: Sử dụng tính chất của đường thẳng song song cách đều.
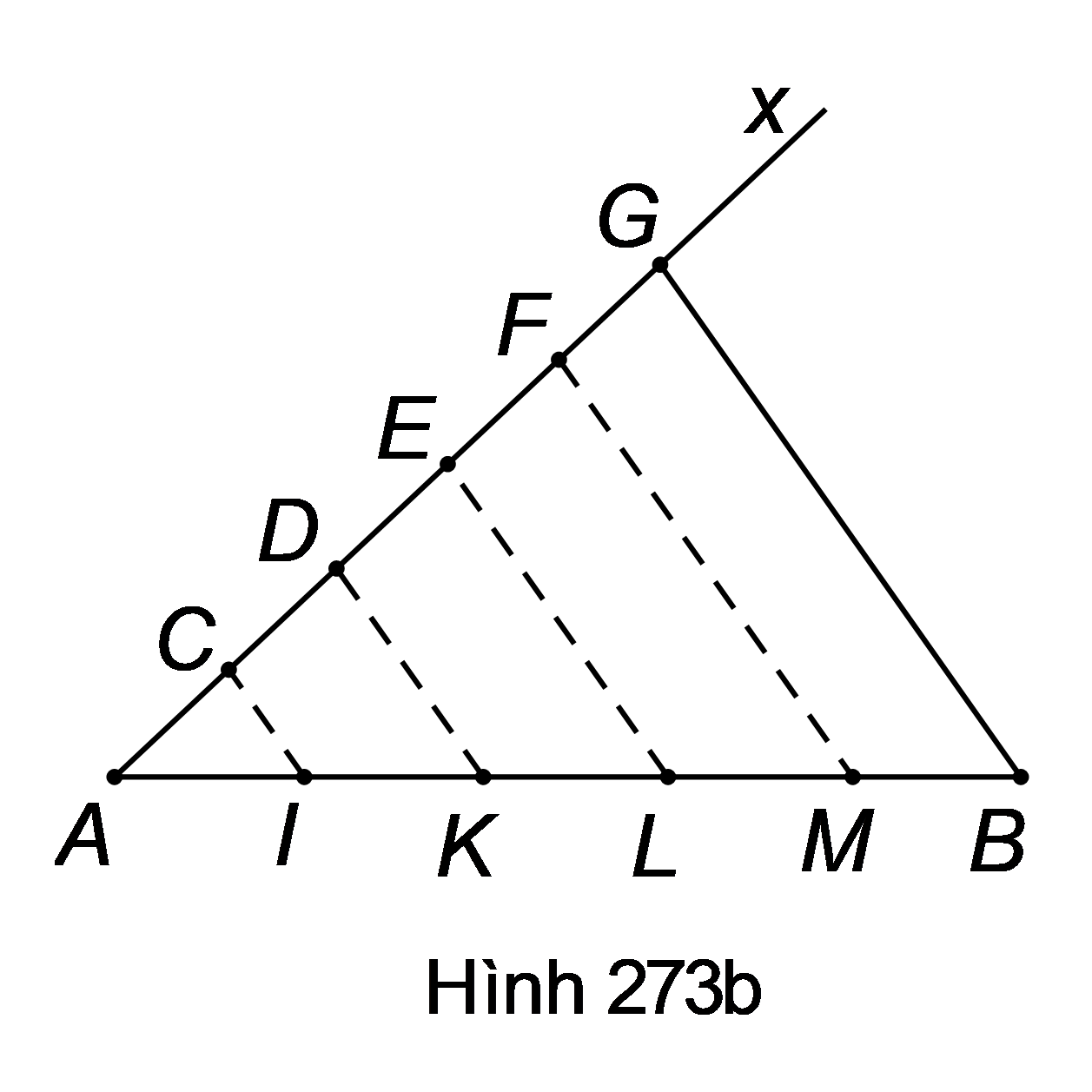
Kẻ tia Ax, trên đó đặt liên tiếp các đoạn thẳng bằng nhau:
.
Nối GB. Từ kẻ các đường thẳng song song với GB, chúng cắt AB lần lượt ở thì CI, là năm đường thẳng song song cách đều nên chúng chắn trên đường thẳng AB những đoạn
thẳng liên tiếp bằng nhau là .