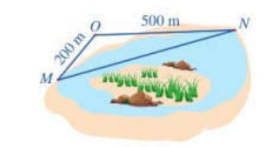
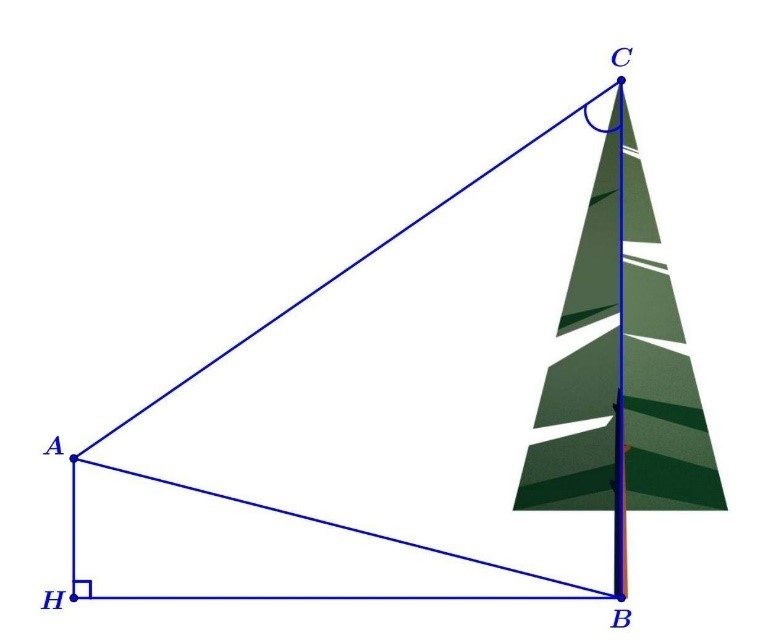
Đề cương ôn tập giữa kì 1 Toán 10 Cánh diều cấu trúc mới có đáp án - Bài Tự luận

Biểu diễn các tập hợp sau trên trục số và tìm \(A \cap B;A \cup B;A\backslash B\).

a) \(A = \left[ { - 3;5} \right)\) và \(B = \left[ {1; + \infty } \right)\).

b) \(A = \left\{ {x \in \mathbb{R}|x \le 3} \right\}\) và \(B = \left\{ {x \in \mathbb{R}| - 2 < x < 2} \right\}\).

Cho 2 tập hợp \(A = \left[ {m - 10\,\,;\,\,m - 2} \right]\) và \(B = \left( {3\,;\,4} \right)\). Tìm tất cả các giá trị của tham số \(m\) để \(A \cap B = \emptyset \).

Cho các tập hợp \(A = \left( { - \infty ;m} \right)\) và \(B = \left[ {3m - 1;3m + 3} \right]\). Tìm \(m\) để:

a) \(A \cap B = \emptyset \);                                                b) \(B \subset A\).

Biểu diễn miền nghiệm của các bất phương trình sau

a) \(2x - 4y \ge 6\);                                                                b) \(x - 3y < 0\).

Một xưởng sản xuất nước mắm, mỗi lít nước mắm loại I cần 3 kg cá và 2 giờ công lao động, đem lại mức lãi là 50 000 đồng; mỗi lít nước mắm loại II cần 2 kg cá và 3 giờ công lao động, đem lại mức lãi 40 000 đồng. Xưởng có 230 kg cá và cần làm việc trong 220 giờ. Hỏi xưởng đó nên sản xuất mỗi loại nước mắm bao nhiêu lít để có mức lãi cao nhất?

Trong một trận lụt ở Hội An, một khách sạn bị nước lụt tràn vào, cần di chuyển cùng một lúc 40 hành khách và 24 vali hành lý. Lúc này, ban quản lí khách sạn chỉ huy động được 8 chiếc ghe lớn và 8 chiếc ghe nhỏ. Một chiếc ghe lớn chỉ có thể chở 10 hành khách và 4 vali hành lý. Một chiếc ghe nhỏ chỉ có thể chở 5 hành khách và 4 vali hành lý. Giá một chuyến ghe lớn là 250 nghìn đồng và giá một chiếc ghe nhỏ là 130 nghìn đồng. Hỏi chủ khách sạn cần thuê bao nhiêu chiếc ghe mỗi loại để chi phí thấp nhất? Tính chi phí thấp nhất đó.

Tính giá trị của các biểu thức sau

a) \(M = \sin 45^\circ .\cos 45^\circ + \sin 30^\circ \); 

b) \(Q = \frac{1}{{{{\sin }^2}120^\circ }} - {\cot ^2}120^\circ \).

Cho \(0^\circ < \alpha < 90^\circ \) thỏa mãn \(\sin \alpha = \frac{3}{5}\). Tính \(\cos \alpha ,\tan \alpha ,\cot \alpha ,\sin \left( {180^\circ - \alpha } \right),\cos \left( {180^\circ - \alpha } \right).\)

Cho tam giác ABC có \(\widehat A = 120^\circ ,b = 8,c = 5\). Tính:

a) Cạnh a và các góc \(\widehat B,\widehat C\).

b) Diện tích tam giác ABC.

c) Bán kính đường tròn ngoại tiếp và đường cao AH của tam giác.

Cho tam giác ABC có \(a = 15;b = 20;c = 25\).

a) Tính diện tích tam giác ABC.

b) Tính bán kính đường tròn ngoại tiếp tam giác ABC.

Để đo khoảng cách giữa hai vị trí M, N ở hai phía ốc đảo, người ta chọn vị trí O bên ngoài ốc đảo sao cho: O không thuộc đường thẳng MN, các khoảng cách OM, ON và góc MON là đo được

Sau khi đo, ta có OM = 200m, ON = 500m, \(\widehat {MON} = 135^\circ \). Khoảng cách giữa hai vị trí M, N là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?

Từ vị trí \(A\) người ta quan sát một cây cao.

Biết \(AH = 4{\rm{m}}\), \(HB = 20{\rm{m}}\), \(\widehat {BAC} = 45^\circ \). Tính chiều cao của cây (làm tròn đến hàng phần mười).

Cho 5 điểm \(A,B,C,D,E\). Chứng minh rằng:

a) \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EA} = \overrightarrow {CB} + \overrightarrow {ED} \).

b) \(\overrightarrow {CD} + \overrightarrow {EA} = \overrightarrow {CA} + \overrightarrow {ED} \).

Cho tam giác ABC. Gọi I là trung điểm của BC, K là trung điểm của BI. Chứng minh rằng:

a) \(\overrightarrow {AK} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AI} ;\)                         

b) \(\overrightarrow {AK} = \frac{3}{4}\overrightarrow {AB} + \frac{1}{4}\overrightarrow {AC} \,.\)

Cho tam giác ABC vuông tại A và có hai cạnh AB = 7, AC = 10

a) Tìm côsin của các góc \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)\) ; \(\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right)\); \(\left( {\overrightarrow {AB} ,\overrightarrow {CB} } \right)\).

b) Gọi H là hình chiếu của A trên BC. Tính \(\overrightarrow {HB} .\overrightarrow {HC} \).

Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} ,\,\,\overrightarrow {{F_2}} = \overrightarrow {MB} \) và \(\overrightarrow {{F_3}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) đều là 100N và \(\widehat {AMB} = 60^\circ .\)

a) Đặt $\overrightarrow{ME}=\overrightarrow{MA}+\overrightarrow{MB}.$ Tính độ dài của đoạn ME.

b) Tìm cường độ và hướng của lực \(\overrightarrow {{F_3}} .\)

Cho hai lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} \), \(\overrightarrow {{F_2}} = \overrightarrow {MB} \) cùng tác động vào một vật tại điểm \(M\) cường độ hai lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \) lần lượt là \(300\left( N \right)\) và \(400\left( N \right)\). \(\widehat {AMB} = 90^\circ \). Tìm cường độ của lực tổng hợp tác động vào vật.