Trắc nghiệm chuyên đề Toán 8 Chủ đề 3. Diện tích tam giác có đáp án
34 người thi tuần này 4.6 729 lượt thi 6 câu hỏi 45 phút
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
6.2 K lượt thi
15 câu hỏi
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
2.7 K lượt thi
15 câu hỏi
10 Bài tập Nhận biết đơn thức, đơn thức thu gọn, hệ số, phần biến và bậc của đơn thức (có lời giải)
1.1 K lượt thi
10 câu hỏi
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
13.8 K lượt thi
18 câu hỏi
Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án (Đề 10)
3.2 K lượt thi
15 câu hỏi
10 Bài tập Tìm giá trị đơn thức khi biết giá trị của biến (có lời giải)
608 lượt thi
10 câu hỏi
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
2.1 K lượt thi
15 câu hỏi
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
3.2 K lượt thi
10 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
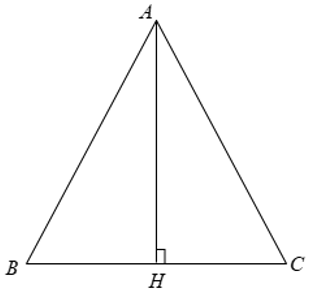
Xét Δ ABC cân tại A có AB = AC = b, BC = a.
Từ A kẻ AH ⊥ BC.
Ta có BH = HC =
Khi đó ta có: SABC =
Áp dụng định lý Py – to – go ta có:
AC2 = AH2 + HC2 ⇒ AH =
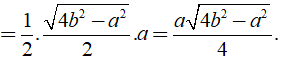
Khi đó SABC =
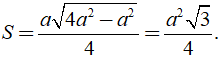
Do đó diện tích của tam giác đều các cạnh bằng a là
Lời giải
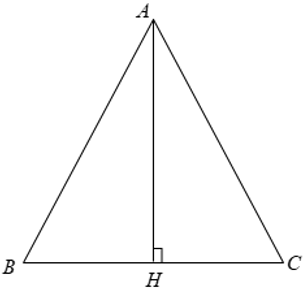
Xét Δ ABC cân tại A có BC = 30( cm )
⇒ BH = CH = 15( cm ).
Áp dụng đinh lý Py – ta – go ta có:
AB = = 25( cm )
Kẻ BK ⊥ AC, giờ ta phải tính BK = ?
Ta có : SABC = AH.BC = .20.30 = 300 ( cm2 )
Mặt khác SABC = .BK.AC = .BK.25
Do đó, ta có .BK.25 = 300 ⇔ BK = = 24( cm ).
Lời giải
Chọn đáp án C.
Ta có diện tích của tam giác: S = b.h.
Trong đó: b là độ dài cạnh đáy, h là độ dài đường cao
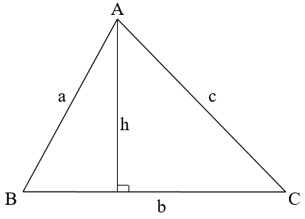
Khi đó ta có : S = .AH.BC = BC.BC = .BC2.
Lời giải
Chọn đáp án B.
Lời giải
Chọn đáp án C.
Áp dụng định lý Py – to – go ta có: AB2 + AC2 = BC2 ⇒ AC = √ (BC2 - AB2)
⇒ AC = √ (52 - 42) = 3cm.
Khi đó SABC = AB.AC = .4.3 = 6( cm2 )
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo