5 câu Trắc nghiệm Toán 10 Cánh diều Bài tập cuối chương 7 (Phần 2) có đáp án (Vận dụng)
20 người thi tuần này 4.6 1.6 K lượt thi 5 câu hỏi 30 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 3
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 2
Đề kiểm tra Ôn tập chương 9 (có lời giải) -Đề 1
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 3
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 2
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 1
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Danh sách câu hỏi:
Câu 1
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
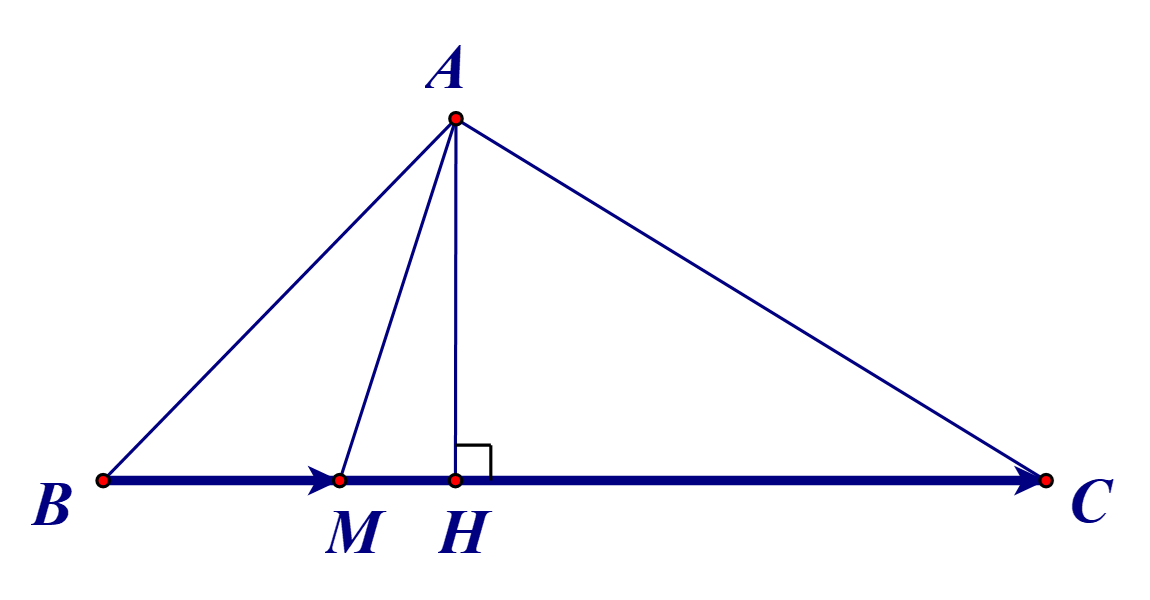
Kẻ AH ⊥ BC tại H.
Ta có:
⦁ \(\overrightarrow {BC} = \left( { - 3; - 3} \right)\). Suy ra \(\frac{1}{4}\overrightarrow {BC} = \left( {\frac{1}{4}.\left( { - 3} \right);\frac{1}{4}.\left( { - 3} \right)} \right) = \left( {\frac{{ - 3}}{4};\frac{{ - 3}}{4}} \right)\);
⦁ \(\overrightarrow {BM} = \left( {x - 2;y - 1} \right)\).
Ta có SABC = 4SABM
Suy ra \(\frac{1}{2}AH.BC = 4.\frac{1}{2}AH.BM\)
Do đó BC = 4BM
Vì vậy \(BM = \frac{1}{4}BC\)
Suy ra \(\overrightarrow {BM} = \frac{1}{4}\overrightarrow {BC} \)
Do đó \(\left\{ \begin{array}{l}x - 2 = - \frac{3}{4}\\y - 1 = - \frac{3}{4}\end{array} \right.\)
Vì vậy \(\left\{ \begin{array}{l}x = \frac{5}{4}\\y = \frac{1}{4}\end{array} \right.\)
Suy ra \({x^2} - {y^2} = {\left( {\frac{5}{4}} \right)^2} + {\left( {\frac{1}{4}} \right)^2} = \frac{{13}}{8}\).
Vậy ta chọn phương án A.
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Chọn A(0; 1) ∈ ∆.
Đường thẳng ∆ có vectơ pháp tuyến \(\vec n = \left( {1;1} \right)\).
Suy ra đường thẳng ∆ nhận \(\vec u = \left( {1; - 1} \right)\) làm vectơ chỉ phương.
Đường thẳng ∆ đi qua A(0; 1) và có vectơ chỉ phương \(\vec u = \left( {1; - 1} \right)\).
Suy ra phương trình tham số của ∆: \(\left\{ \begin{array}{l}x = t\\y = 1 - t\end{array} \right.\)
Ta có M ∈ ∆. Suy ra M(t; 1 – t).
Ta có \(\overrightarrow {NM} = \left( {t + 1; - 2 - t} \right)\).
Suy ra \(NM = \left| {\overrightarrow {NM} } \right| = \sqrt {{{\left( {t + 1} \right)}^2} + {{\left( { - 2 - t} \right)}^2}} \).
Theo đề, ta có MN = 5.
⇔ (t + 1)2 + (–2 – t)2 = 25.
⇔ t2 + 2t + 1 + 4 + 4t + t2 = 25.
⇔ 2t2 + 6t – 20 = 0.
⇔ t = 2 hoặc t = –5.
Với t = 2, ta có tọa độ M(2; –1).
Với t = –5, ta có tọa độ M(–5; 6).
Vậy ta chọn phương án A.
Câu 3
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
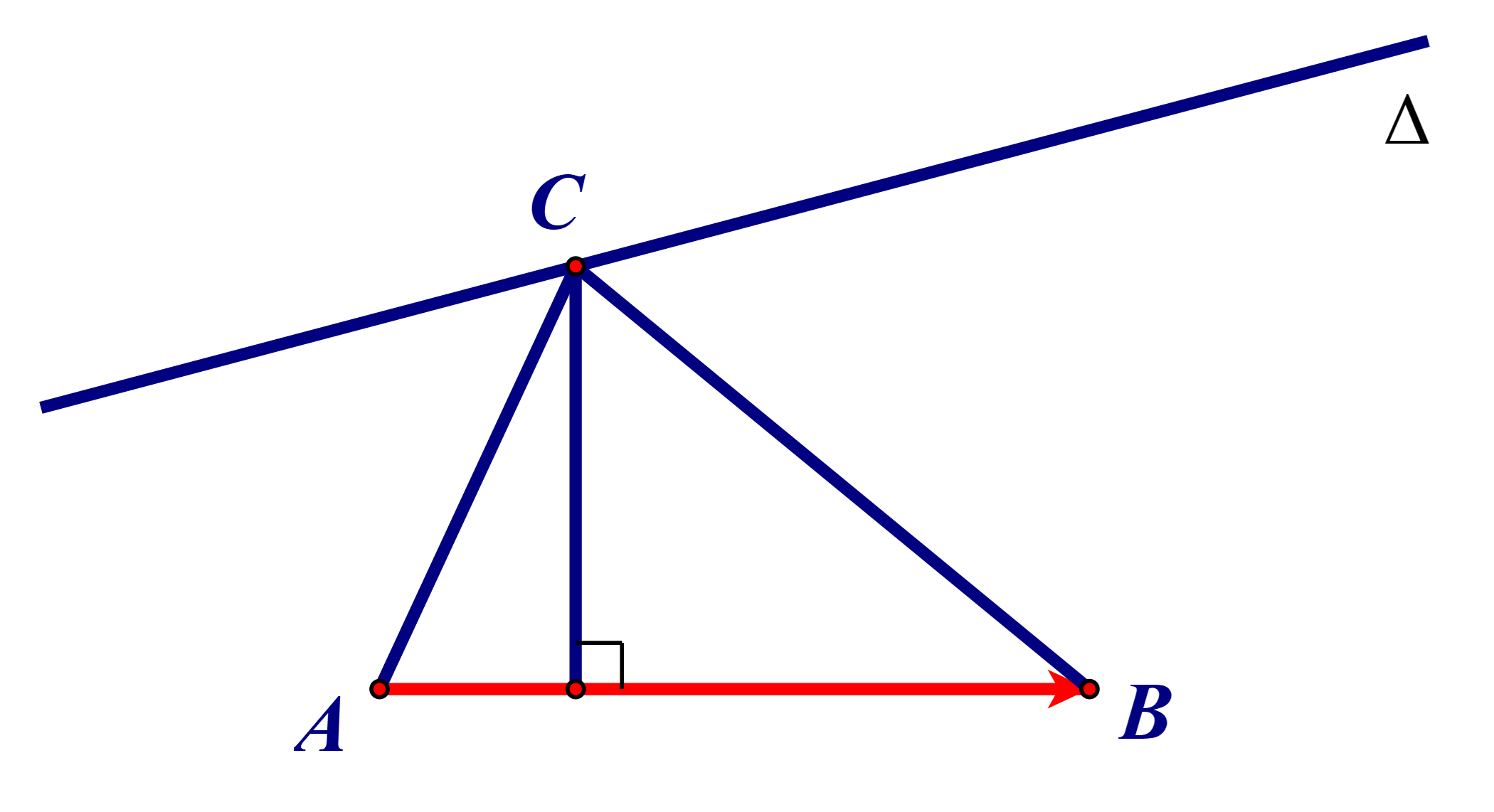
Ta có \(\overrightarrow {AB} = \left( {3; - 1} \right)\). Suy ra \(AB = \sqrt {{3^2} + {{\left( { - 1} \right)}^2}} = \sqrt {10} \).
Đường thẳng AB có vectơ chỉ phương \(\overrightarrow {AB} = \left( {3; - 1} \right)\).
Suy ra đường thẳng AB có vectơ pháp tuyến \({\vec n_{AB}} = \left( {1;3} \right)\).
Đường thẳng AB đi qua A(2; 2) và có vectơ chỉ phương \(\overrightarrow {AB} = \left( {3; - 1} \right)\).
Suy ra phương trình tổng quát của AB: 1(x – 2) + 3(y – 2) = 0.
⇔ x + 3y – 8 = 0.
Đường thẳng ∆ đi qua điểm M(–8; 0) và có vectơ chỉ phương \({\vec u_\Delta } = \left( {2;1} \right)\).
Suy ra phương trình tham số của ∆: \(\left\{ \begin{array}{l}x = - 8 + 2t\\y = t\end{array} \right.\)
Ta có C ∈ ∆. Suy ra tọa độ C(2t – 8; t).
Theo đề, ta có diện tích tam giác ABC bằng 17.
\( \Leftrightarrow \frac{1}{2}d\left( {C,AB} \right).AB = 17\).
\( \Leftrightarrow \frac{1}{2}.\frac{{\left| {2t - 8 + 3t - 8} \right|}}{{\sqrt {{1^2} + {3^2}} }}.\sqrt {10} = 17\)
⇔ |5t – 16| = 34
\( \Leftrightarrow \left[ \begin{array}{l}5t - 16 = 34\\5t - 16 = - 34\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}t = 10\\t = - \frac{{18}}{5}\end{array} \right.\)
Với t = 10, ta có C(12; 10).
Với \(t = - \frac{{18}}{5}\), ta có \(C\left( { - \frac{{76}}{5}; - \frac{{18}}{5}} \right)\).
Vậy C(12; 10) hoặc \(C\left( { - \frac{{76}}{5}; - \frac{{18}}{5}} \right)\) thỏa mãn yêu cầu bài toán.
Do đó ta chọn phương án B.
Câu 4
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Đường tròn (C) có tâm I(–1; 3), bán kính \(R = \sqrt {{{\left( { - 1} \right)}^2} + {3^2} - 5} = \sqrt 5 \).
Gọi ∆ là tiếp tuyến cần tìm.
Đường thẳng d có vectơ pháp tuyến \({\vec n_d} = \left( {1;2} \right)\).
Vì ∆ // d nên ∆ nhận \({\vec n_d} = \left( {1;2} \right)\) làm vectơ pháp tuyến.
Suy ra phương trình ∆ có dạng: x + 2y + c = 0.
Vì d là tiếp tuyến của (C) nên d(I, ∆) = R.
\( \Leftrightarrow \frac{{\left| { - 1 + 2.3 + c} \right|}}{{\sqrt {{1^2} + {2^2}} }} = \sqrt 5 \)
⇔ |c + 5| = 5
⇔ c + 5 = 5 hoặc c + 5 = –5
⇔ c = 0 hoặc c = –10.
Vậy có 2 phương trình tiếp tuyến d thỏa mãn yêu cầu bài toán có phương trình là: x + 2y = 0 hoặc x + 2y – 10 = 0.
Do đó ta chọn phương án A.
Câu 5
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
Tọa độ giao điểm của đường thẳng d và elip (E) thỏa mãn hệ phương trình: \[\left\{ \begin{array}{l}x = - 4\\\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\end{array} \right.\]
\( \Leftrightarrow \left\{ \begin{array}{l}x = - 4\\\frac{{{{\left( { - 4} \right)}^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x = - 4\\{y^2} = \frac{{81}}{{25}}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x = - 4\\y = \pm \frac{9}{5}\end{array} \right.\)
Suy ra tọa độ \(M\left( { - 4; - \frac{9}{5}} \right),\,\,N\left( { - 4;\frac{9}{5}} \right)\).
Khi đó \(MN = \sqrt {{{\left( { - 4 + 4} \right)}^2} + {{\left( {\frac{9}{5} + \frac{9}{5}} \right)}^2}} = \frac{{18}}{5}\).
Vậy ta chọn phương án C.