8 câu Trắc nghiệm Toán 10 Cánh Diều Hệ bất phương trình bậc nhất hai ẩn (Thông hiểu) có đáp án

Hướng dẫn giải

Đáp án đúng là: B

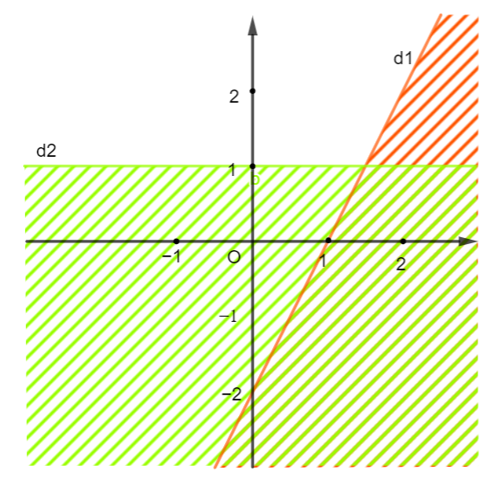
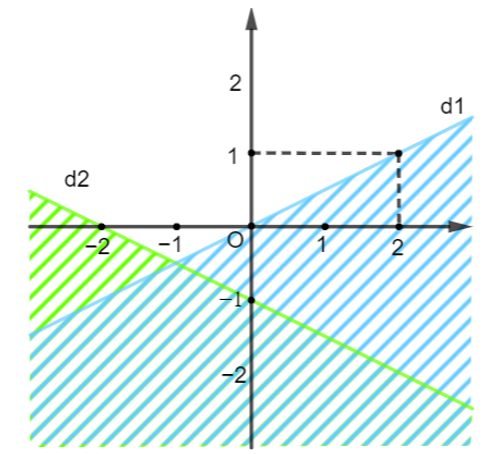
Xét đường thẳng d₁: y = a₁x + b₁ đi qua điểm (1; 0) và (0; −2) nên ta có :

Vậy (d₁): y = 2x – 2 ⇔ 2x − y − 2 = 0.

Thay điểm (0; 2) thuộc miền nghiệm vào (d_1­) ta được:

2 . 0 − 2 − 2 < 0

Do đó ta có bất phương trình 2x − y − 2 < 0 (không kể đường thẳng d₁) (1)

Xét đường thẳng d₂: y = a₂x + b₂ đi qua điểm (1; 1) và (0; 1) nên ta có :

$\left\{\begin{array}{c}1=1a_2+b_2\\ 1=0a_2+b_2\end{array}\right.\iff \left\{\begin{array}{c}{a}_2=0\\ b_2=1\end{array}\right.$

Vậy (d₂): y = 1.

Thay điểm (0; 2) thuộc miền nghiệm vào (d_2­) ta được:

2 > 1

Do đó ta có bất phương trình y ≥ 1 (kể cả đường thẳng d₂) (2)

Từ (1) và (2) ta có hệ bất phương trình cần tìm là: $\left\{\begin{array}{c}2x-y-2<0\\ y\ge 1\end{array}\right.$ .

Hướng dẫn giải

Đáp án đúng là: C

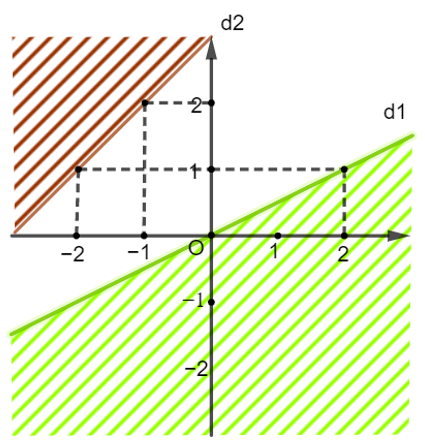
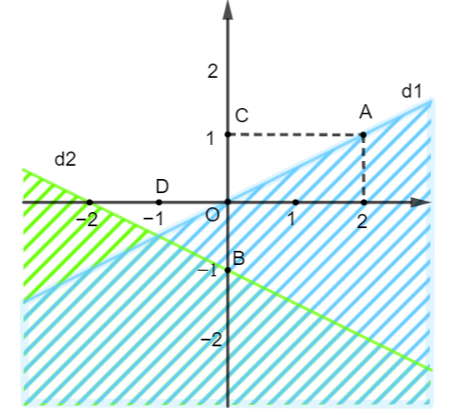
Xét đường thẳng d₁: y = a₁x + b₁ đi qua điểm (0; 0) và (2; 1) nên ta có :

$\left\{\begin{array}{c}0=0a_1+b_1\\ 1=2a_1+b_1\end{array}\right.\iff \left\{\begin{array}{c}{a}_1=\frac{1}{2}\\ b_1=0\end{array}\right.$

Vậy (d₁): y = $\frac{1}{2}$ x  ⇔$\frac{1}{2}$ x − y = 0.

Thay điểm (0; 1) thuộc miền nghiệm vào (d_1­) ta được:

 $\frac{1}{2}$. 0 − 1 < 0

Do đó ta có bất phương trình $\frac{1}{2}$ x − y < 0  (không kể đường thẳng d₁) (1)

Xét đường thẳng d₂: y = a₂x + b₂ đi qua điểm (−1; 2) và (−2; 1) nên ta có :

$\left\{\begin{array}{c}2=-1a_2+b_2\\ 1=-2a_2+b_2\end{array}\right.\iff \left\{\begin{array}{c}{a}_2=1\\ b_2=3\end{array}\right.$

Vậy (d₂): y = x + 3.

Thay điểm (0; 2) thuộc miền nghiệm vào (d_2­) ta được:

2 < 0 + 3

Do đó ta có bất phương trình y < x + 3 (không kể đường thẳng d₂)  (2)

Từ (1) và (2) ta có hệ bất phương trình $\left\{\begin{array}{c}\frac{1}{2}x-y<0\\ y<x+3\end{array}\right.$ .

Hướng dẫn giải

Đáp án đúng là: B

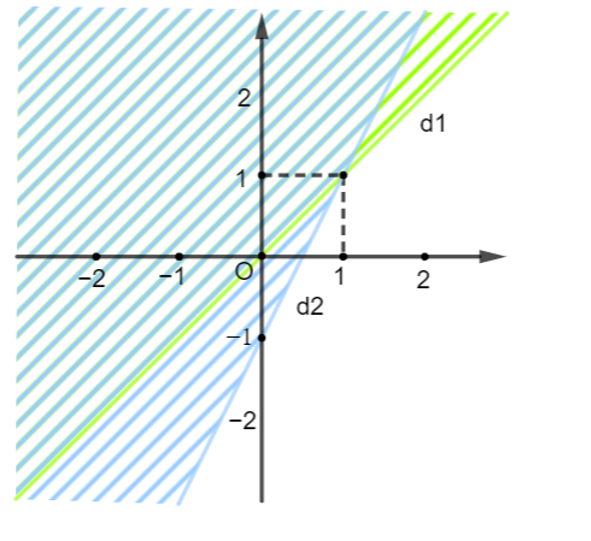
Thay (3; −1) vào bất phương trình (1) ta được:

3 − 5 . (−1) > 0 ⇔ 8 > 0 (luôn đúng)

Thay (3; −1) vào bất phương trình (2) ta được:

3 − 1 − 1 < 0 ⇔ 2 < 0 (vô lí)

Vậy điểm A thuộc miền nghiệm của (1) nhưng không thuộc miền nghiệm của (2).

Hướng dẫn giải

Đáp án đúng là: A

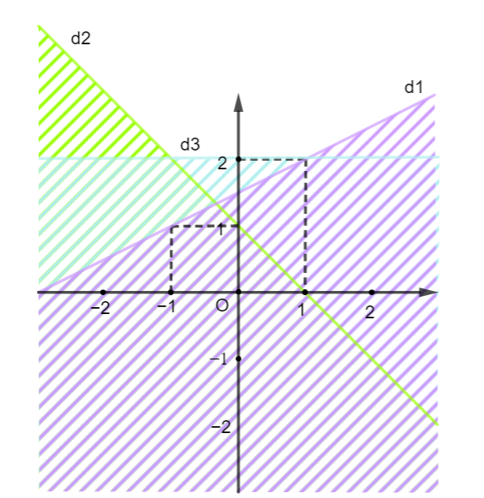
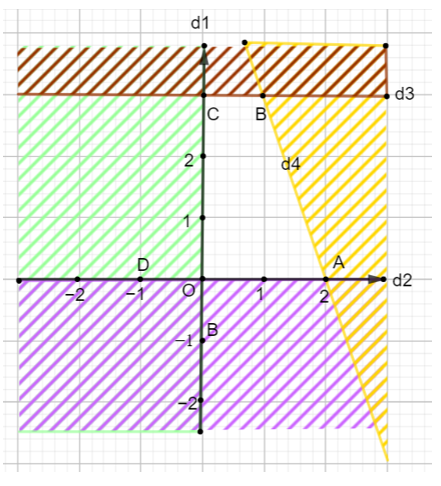
Xét đường thẳng d₁: y = a₁x + b₁ đi qua điểm (1; 2) và (−1; 1) nên ta có :

$\left\{\begin{array}{c}2=1a_1+b_1\\ 1=-1a_1+b_1\end{array}\right.\iff \left\{\begin{array}{c}{a}_1=\frac{1}{2}\\ b_1=\frac{3}{2}\end{array}\right.$

Vậy (d₁): y =$\frac{1}{2}$ x + $\frac{3}{2}$  ⇔ −x + 2y = 3.

Thay điểm (0; 3) thuộc miền nghiệm vào (d_1­) ta được:

−0 + 2 . 3 > 3

Do đó ta có bất phương trình −x + 2y > 3 (không kể đường thẳng d₁) (1)

Xét đường thẳng d₂: y = a₂x + b₂ đi qua điểm (0; 1) và (1; 0) nên ta có :

$\left\{\begin{array}{c}1=0a_2+b_2\\ 0=1a_2+b_2\end{array}\right.\iff \left\{\begin{array}{c}{a}_2=-1\\ b_2=1\end{array}\right.$

Vậy (d₂): y =  −x + 1 ⇔ x + y − 1 = 0

Thay điểm (0; 3) thuộc miền nghiệm vào (d_2­) ta được:

0 + 3 − 1 > 0

Do đó ta có bất phương trình x + y − 1 > 0 (không kể đường thẳng d₂)  (2)

Xét đường thẳng d₃: y = a₃x + b₃ đi qua điểm (0; 2) và (1; 2) nên ta có :

$\left\{\begin{array}{c}2=0a_1+b_1\\ 2=1a_1+b_1\end{array}\right.\iff \left\{\begin{array}{c}{a}_1=0\\ b_1=2\end{array}\right.$

Vậy (d₃): y = 2.

Thay điểm (0; 3) thuộc miền nghiệm vào (d_3­) ta được:

3 > 2

Do đó ta có bất phương trình y > 2 (không kể đường thẳng d₃) (3)

Từ (1), (2), (3) ta có hệ bất phương trình $\left\{\begin{array}{c}-x+2y>3\\ x+y-1>0\\ y>2\end{array}\right.$ .

Hướng dẫn giải

Đáp án đúng là: D

Điểm (2; 0) nằm trên mặt phẳng không bị gạch nên (2; 0) thuộc miền nghiệm của hệ bất phương trình trên.