Dạng 3. Chứng minh hai đường thẳng song song
34 người thi tuần này 4.6 3.7 K lượt thi 3 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 10
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 09
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 08
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 07
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 06
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 05
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 04
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 03
Danh sách câu hỏi:
Lời giải
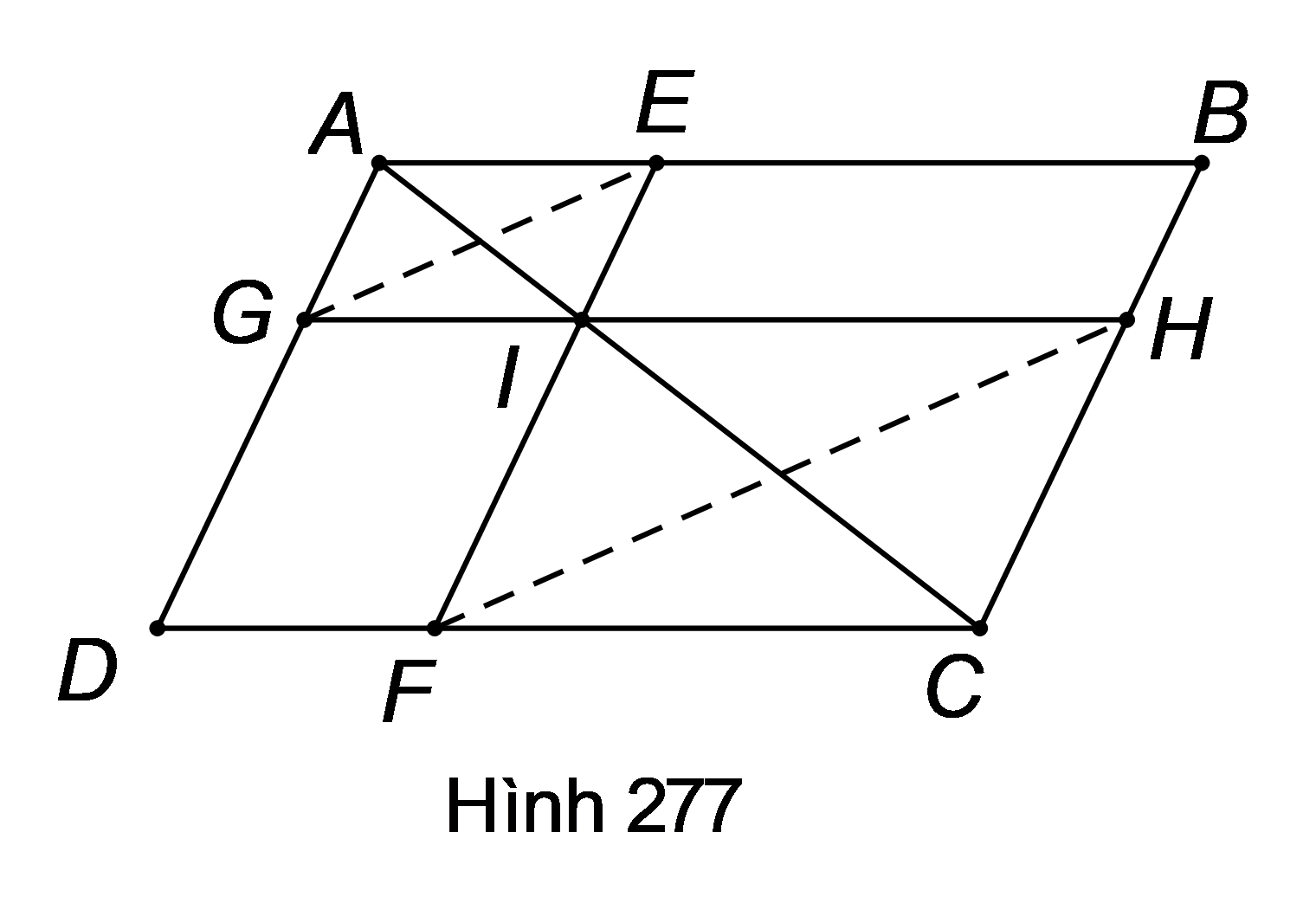
ABCD là hình bình hành nên và , suy ra .
Áp dụng hệ quả của định lí Ta-lét cho và , ta được:
.
Điều này chứng tỏ đường thẳng EG cắt hai cạnh của tam giác IHF và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ, nên (theo định lí Ta-lét đảo).
Lời giải
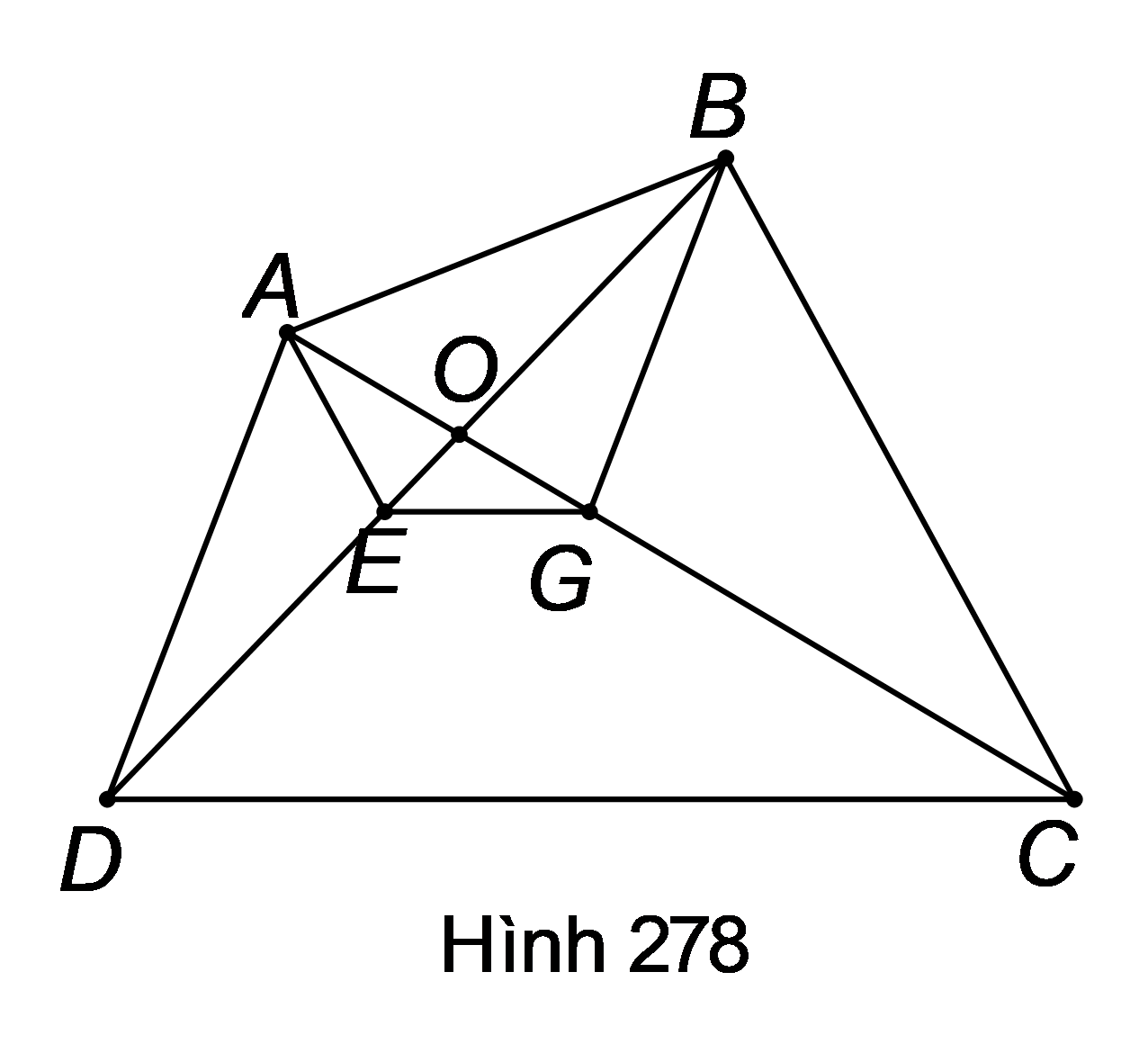
Áp dụng hệ quả của định lí Ta-lét cho và , ta được:
(1); (2).
Nhân theo vế các đẳng thức (1) và (2), ta được:
.
Điều này chứng tỏ đường thẳng EG cắt hai cạnh của tam giác OCD và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ nên (theo định lí Ta-lét đảo).
Lời giải
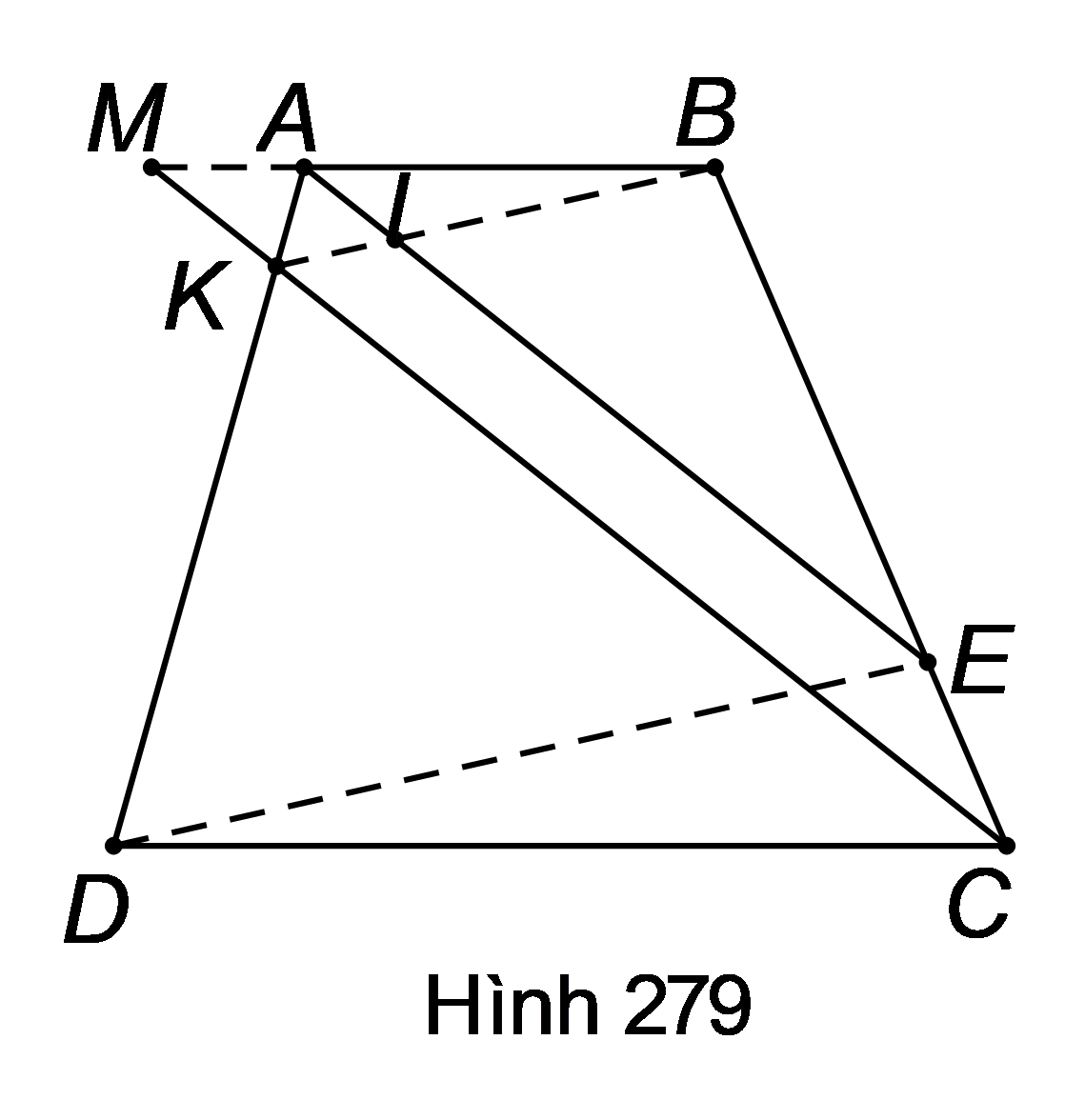
Gọi I,M lần lượt là giao điểm của AE với BK và CK với AB.
Áp dụng hệ quả của định lí Ta-lét cho và , thu được:
(1).
Áp dụng hệ quả của định lí Ta-lét cho , ta được:
(2).
Từ (1) và (2) suy ra . Điều này chứng tỏ đường thẳng KI cắt hai cạnh của tam giác ADE và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ nên , hay (theo định lí Ta-lét đảo).