Dạng 3. Sử dụng phối hợp đường trung bình của tam giác và đường trung bình của hình thang đê chứng minh có đáp án
32 người thi tuần này 4.6 4.2 K lượt thi 4 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 10
365 lượt thi
9 câu hỏi
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 09
319 lượt thi
9 câu hỏi
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 08
318 lượt thi
9 câu hỏi
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 07
312 lượt thi
9 câu hỏi
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 06
311 lượt thi
9 câu hỏi
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 05
317 lượt thi
11 câu hỏi
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 04
317 lượt thi
11 câu hỏi
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 03
318 lượt thi
11 câu hỏi
Danh sách câu hỏi:
Lời giải
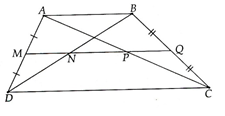
a) Ta có MN là đường trung bình của tam giác ABD
=> MN // AB
Tương tự, ta được MP//CD và MQ//AB, CD.
Như vậy, MN, MP, MQ cùng song song AB Þ ĐPCM.
Lời giải
b) Ta có:
Lời giải
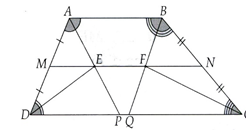
a) Gọi P và Q lần lượt là giao điểm của AE, AF với CD.
Chứng minh tương tự 4.
Lời giải
b) Ta có:
Lại có:
c = CD = CQ + QD = BC + QD = b + QD (do tam giác BCQ cân) Þ QD = c - b.Trong hình thang ABQD có M là trung điểm của AD và MF//DQ nên chứng minh được F là trung điểm của BQ, từ đó chứng minh MF là đường trung bình của hình thang ABQD.
Vì MF là đường trung bình của hình thang ABQD.
Þ
Mặt khác, FN là đường trung bình của tam giác BCQ, tức là
Nhắn tin Zalo
Hỏi bài tập