Đề thi Giữa kì 1 Toán 8 có đáp án (Đề 4)
27 người thi tuần này 4.6 7.3 K lượt thi 4 câu hỏi 30 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 10
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 09
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 08
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 07
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 06
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 05
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 04
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 03
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải
1) (x – 4)x – (x – 3)2= 0
x2– 4x – x2+ 6x – 9 = 0
2x – 9 = 0
2x = 9
x = 4,5
Vậy tập nghiệm của phương trình là S = {4,5}.
2) 3x – 6 = x2– 16
x2– 16 – 3x + 6 = 0
x2– 3x – 10 = 0
x2+ 2x – 5x – 10 = 0
x(x + 2) – 5(x + 2) = 0
(x + 2)(x – 5) = 0
\( \Rightarrow \left[ \begin{array}{l}x + 2 = 0\\x - 5 = 0\end{array} \right.\)
\( \Rightarrow \left[ \begin{array}{l}x = - 2\\x = 5\end{array} \right.\)
Vậy tập nghiệm của phương trình là S = {–2; 5}.
Lời giải
Hướng dẫn giải
A(x) = 2x3+ x2– 4x + m
\[ = 2{x^3}--{x^2} + 2{x^2}--x--3x + \frac{3}{2} - \frac{3}{2} + m\]
\[ = {x^2}\left( {2x--1} \right) + x\left( {2x--1} \right)--\frac{3}{2}\left( {2x - 1} \right) - \frac{3}{2} + m\]
\[ = \left( {2x--1} \right)\left( {{x^2} + x - \frac{3}{2}} \right) - \frac{3}{2} + m\]
Để A(x) ⋮ B(x) thì \( - \frac{3}{2} + m = 0\)\( \Leftrightarrow m = \frac{3}{2}\)
Vậy \(m = \frac{3}{2}\) thì đa thức A(x) ⋮ B(x).
Lời giải
Hướng dẫn giải
1) \(\frac{{x - 5}}{{x - 2}} - \frac{{x + 4}}{{2x - {x^2}}}\)
\( = \frac{{x - 5}}{{x - 2}} + \frac{{x + 4}}{{{x^2} - 2x}}\)
\( = \frac{{x - 5}}{{x - 2}} + \frac{{x + 4}}{{x\left( {x - 2} \right)}}\)
\( = \frac{{x\left( {x - 5} \right)}}{{x\left( {x - 2} \right)}} + \frac{{x + 4}}{{x\left( {x - 2} \right)}}\)
\( = \frac{{{x^2} - 5x + x + 4}}{{x\left( {x - 2} \right)}}\)
\( = \frac{{{x^2} - 4x + 4}}{{x\left( {x - 2} \right)}}\)
\( = \frac{{{{\left( {x - 2} \right)}^2}}}{{x\left( {x - 2} \right)}}\)
\( = \frac{{x - 2}}{x}\)
2) \(\frac{{x - 3}}{{x + 2}} + \frac{{4x}}{{x - 3}} - \frac{{8x + 4{x^2}}}{{{x^2} - x - 6}}\)
\( = \frac{{x - 3}}{{x + 2}} + \frac{{4x}}{{x - 3}} - \frac{{8x + 4{x^2}}}{{\left( {x - 3} \right)\left( {x + 2} \right)}}\)
\( = \frac{{{{\left( {x - 3} \right)}^2}}}{{x + 2}} + \frac{{4x\left( {x + 2} \right)}}{{x - 3}} - \frac{{8x + 4{x^2}}}{{\left( {x - 3} \right)\left( {x + 2} \right)}}\)
\( = \frac{{{{\left( {x - 3} \right)}^2} + 4{x^2} + 8x - 8x - 4{x^2}}}{{\left( {x - 3} \right)\left( {x + 2} \right)}}\)
\( = \frac{{{{\left( {x - 3} \right)}^2}}}{{\left( {x - 3} \right)\left( {x + 2} \right)}}\)
\( = \frac{{x - 3}}{{x + 2}}\)
Lời giải
Hướng dẫn giải
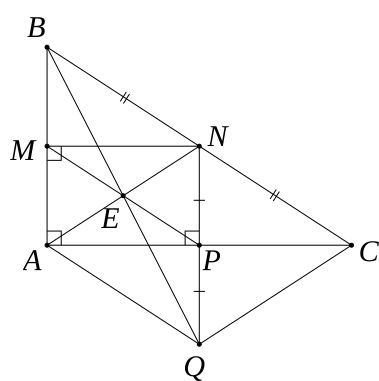
1) Xét tứ giác AMNP, có: \(\widehat {MAN} = \widehat {AMN} = \widehat {APN} = 90^\circ \)
Do đó tứ giác AMNP là hình chữ nhật.
Ta có: \(\left\{ \begin{array}{l}NP \bot AC\\AB \bot AC\end{array} \right. \Rightarrow NP//AB\)
Xét tam giác ABC có: N là trung điểm của BC và NP // AB
Suy ra P là trung điểm của AC.
Vì N đối xứng với Q qua AC nên P là trung điểm của AC.
Xét tứ giác ANCQ có hai đường chéo AC và NQ cắt nhau tại trung điểm P của mỗi đường
Suy ra tứ giác ANCQ là hình bình hành
Mà có \(AC \bot NQ\) (gt)
Vậy tứ giác ANCQ là hình thoi
2) Ta có AMNP là hình chữ nhật có AN cắt MP tại E
Suy ra E là trung điểm của AN và MP
Xét tam giác ABC có: N, P là trung điểm của BC, AC
Nên NP là đường trung bình trong tam giác ABC.
\( \Rightarrow NP = \frac{1}{2}AB\)
mà \(NP = \frac{1}{2}NQ\) (vì P là trung điểm của NQ)
⇒ AB = NQ
Xét tứ giác ABNQ có: NQ = AB (cmt) và NQ // AB (vì NP // AB)Suy ra ABNQ là hình bình hànhmà E là trung điểm của AN (cmt)Nên E cũng là trung điểm của BQVậy 3 điểm B, E, Q thẳng hàng
3) Vì ABNQ là hình bình hành nên AQ // BN
Hay AQ // BC
Do đó ABCQ là hình thang.
Vì ABNQ là hình thoi nên CA là phân giác của góc QCN
\( \Rightarrow \widehat {ACB} = \widehat {ACQ} = \frac{1}{2}\widehat {QCB}\) hay \(\widehat {QCB} = 2\widehat {ACB}\)
Để hình thang ABCQ là hình thang cân thì \(\widehat {ABC} = \widehat {QCB}\)
Mà \(\widehat {QCB} = 2\widehat {ACB}\)
\( \Rightarrow \widehat {ABC} = 2\widehat {ACB}\)
Xét ΔABC vuông tại A có: \(\widehat {ABC} + \widehat {ACB} = 90^\circ \)
\( \Rightarrow 2\widehat {ACB} + \widehat {ACB} = 90^\circ \)
\( \Rightarrow 3\widehat {ACB} = 90^\circ \)
\( \Rightarrow \widehat {ACB} = 30^\circ \)
Vậy tam giác ABC có \(\widehat {ACB} = 30^\circ \) thì ABCQ là hình thang cân.