Dạng 4: Góc có đỉnh ở bên trong hay bên ngoài đường tròn có đáp án
23 người thi tuần này 4.6 3.6 K lượt thi 9 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
12 bài tập Một số bài toán thực tế liên quan đến độ dài cung tròn, diện tích hình quạt tròn và hình vành khuyên có lời giải
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
15 câu trắc nghiệm Toán 9 Kết nối tri thức Bài 13. Mở đầu về đường tròn có đáp án
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
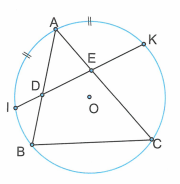
a) Ta thấy là góc có đỉnh D nằm trong đường tròn nên:
. (1)
Mà là góc nội tiếp chắn cung nên: . (2)
Từ (1) và (2) suy ra .
Lời giải
b) Tứ giác DECB là hình thang cân
là hình thang và
cân tại A.
Vậy tam giác ABC phải là tam giác cân tại A thì tứ giác DECB là hình thang cân.
Lời giải
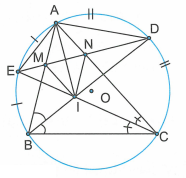
a) Theo giả thiết BD là tia phân giác của góc nên D là điểm chính giữa của cung . (1)
Tương tự ta cũng có E là điểm chính giữa của cung
. (2)
Góc và là hai góc có đỉnh nằm trong đường tròn (O) nên:
và . (3)
Từ (1), (2) và (3) suy ra cân tại A.
Lời giải
b) Ta có (góc ngoài của tam giác AIC). (4)
(hai góc nội tiếp cùng chắn hai cung bằng nhau là ). (5)
Vì I giao điểm hai đường phân giác của , suy ra AI là đường phân giác của góc
. (6)
Từ (4), (5) và (6) suy ra cân tại E.
Chứng minh hoàn toàn tương tự, ta cũng có cân tại D.
Lời giải
c) Vì AI là đường phân giác của cân tại A nên AI vuông góc với MN tại trung điểm của MN.
Tương tự, cân tại D nên MN vuông góc với AI tại trung điểm của AI.
Do đó AMIN là hình thoi vì có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.