Đề kiểm tra giữa học kì 2 môn Toán 9 ( Mới nhất)_ đề 1
48 người thi tuần này 4.6 20 K lượt thi 6 câu hỏi 90 phút
- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
12 bài tập Một số bài toán thực tế liên quan đến độ dài cung tròn, diện tích hình quạt tròn và hình vành khuyên có lời giải
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
15 câu trắc nghiệm Toán 9 Kết nối tri thức Bài 13. Mở đầu về đường tròn có đáp án
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
a) 3x2 + 10x + 3 = 0
Tính ∆ = b2 – 4ac. Phương trình có các hệ số là a = 3; b = 10; c = 3.
∆ = 102 – 4.3.3 = 100 – 36 = 64 > 0.
Do ∆ > 0, áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt:
x1 = ; x2 = .
Vậy phương trình có tập nghiệm là S =.
b) –x4 + 2020x2 + 2021 = 0
Û –x4 – x2 + 2021x2 + 2021 = 0
Û –x2(x2 + 1) + 2021(x2 + 1) = 0
Û – (x2 – 2021)(x2 + 1) = 0
Û (x2 + 1) = 0 (vô lý) hoặc (x2 – 2021) = 0
Û x2 = 2021
Û x = ±
Vậy phương trình có hai nghiệm là ±.
c) x3 – 5x2 + 4x = 0
Û x(x2 – 5x + 4) = 0
Û x(x2 – x – 4x + 4) = 0
Û x[x(x – 1) – 4(x – 1)] = 0
Û x(x – 1)(x – 4) = 0
Û
Vậy phương trình đã cho có tập nghiệm là S = {0; 1; 4}.
Lời giải
a) Bảng giá trị:
|
x |
–2 |
–1 |
0 |
1 |
2 |
|
y = x2 |
4 |
1 |
0 |
1 |
4 |
Trên mặt phẳng tọa độ lấy các điểm A(–2; 4); B(–1; 1); O(0; 0); C(1; 1); D(2; 4).
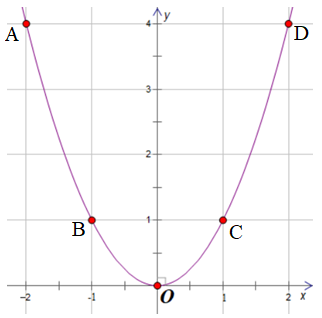
b) Phương trình hoành độ giao điểm của (P) và (d) là:
x2 = –x + 2
Û x2 + x – 2 = 0
Û x2 + 2x – x – 2 = 0
Û x( x + 2) – (x + 2) = 0
Û (x – 1)(x + 2) = 0
Û
• Với x = 1 thì y = –x + 2 = –1 + 2 = 1.
Do đó, ta có tọa độ giao điểm của (P) và (d) là A(1; 1).
• Với x = –2 thì y = –x + 2 = –(–2) + 2 = 4.
Do đó, ta có tọa độ giao điểm của (P) và (d) là B(–2; 4).
Vậy hai đồ thị hàm số trên có 2 giao điểm là A(1;1) và B(–2; 4).
Lời giải
a) Ta có: ∆ = m2 – 4.2.(–5) = m2 + 40
Vì ∆ = m2 + 40 > 0 (đúng với mọi giá trị của m).
Nên phương trình (1) luôn có 2 nghiệm với mọi m (điều phải chứng minh).
b) A = x12 – x1 + x22 – x2
= (x12 + x22) – (x1 + x2)
= (x1 + x2)2 – 2x1.x2 – (x1 + x2) (2)
Theo hệ thức Vi-et, ta có:
Thay vào (2) ta được:
A = =.
Lời giải
Gọi x là số giáo viên, y là số học sinh (điều kiện: x, y ∈ ℕ, 0 < x, y < 330).
Vì tổng số giáo viên và học sinh đi tham quan là 330 người nên: x + y = 330 (1)
Tổng số tiền vé của giáo viên khi chưa giảm là: 40 000x (đồng).
Tổng số tiền vé của học sinh khi chưa giảm là: 20 000y (đồng).
Tổng số tiền vé của giáo viên và học sinh khi chưa giảm là:
40 000x + 20 000y (đồng).
Mỗi vé tham quan được giảm 10%, tức là giá vé sau khi giảm bằng 90% giá vé ban đầu.
Tổng số tiền vé nhà trường chi trả là 6 480 000 đồng nên ta có phương trình:
90%.(40 000x + 20 000y) = 6 480 000
Û 40 000x + 20 000y = 7 200 000
Û x + 2y = 360 (2)
Từ (1) và (2), ta có hệ phương trình:
Û
Û
Û
Û
Û (thỏa mãn)
Vậy số giáo viên là 30 người và số học sinh là 300 người.
Lời giải
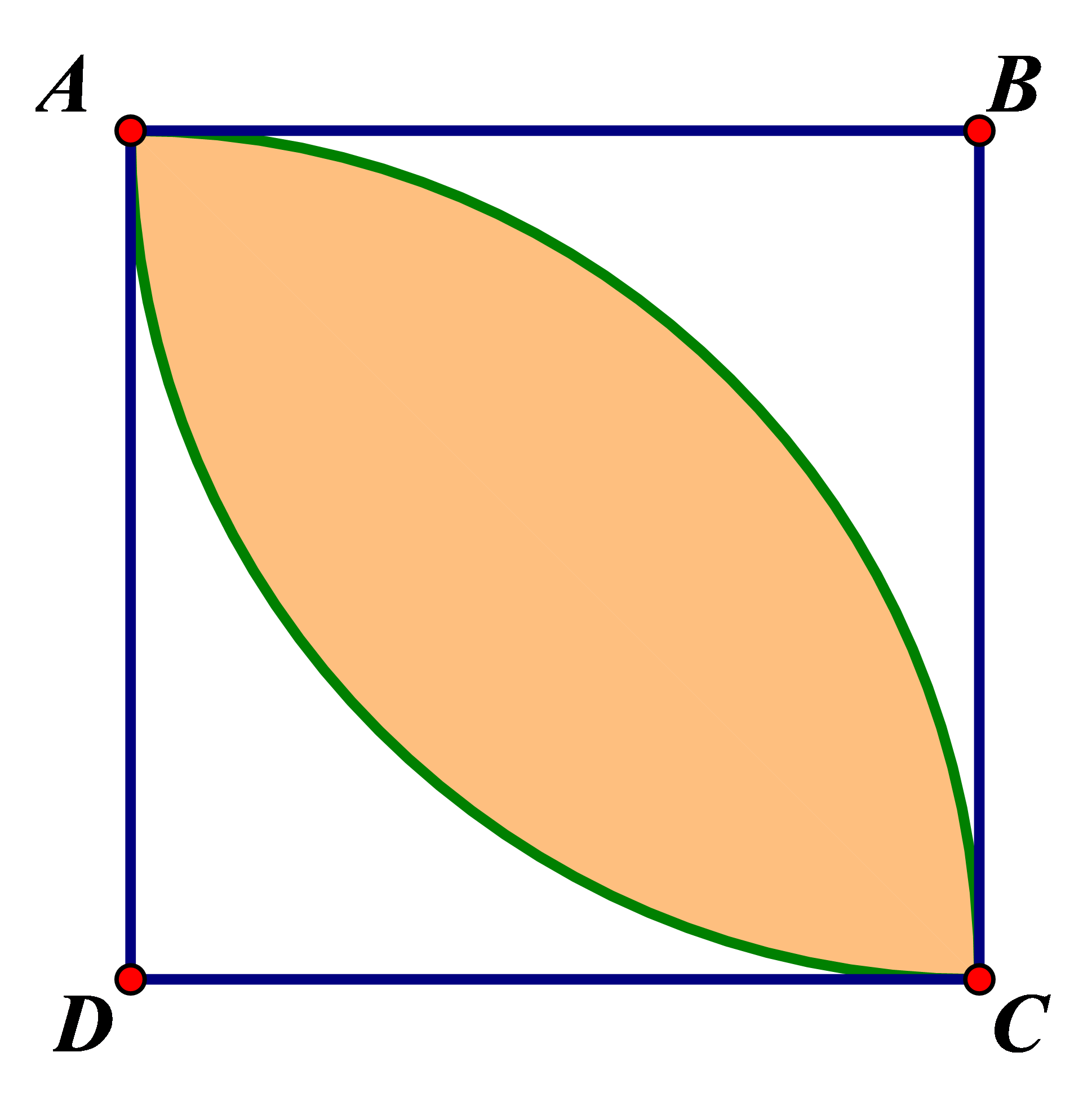
Gọi S là diện tích được tạo ra bởi cung tròn AC và dây AC của đường tròn tâm D.
S = diện tích quạt DAC – diện tích tam giác ADC.
Vì ABCD là hình vuông nên . Do đó:
Diện tích quạt DAC là:
πR2.≈ 3,14.252.≈ 490,625 (cm2).
Diện tích tam giác ADC là:
= =312,5 (cm2)
Diện tích cần tính bằng:
2S ≈ 2.(490,625 – 312,5) ≈ 356,25 ≈ 356,3 (cm2).
Phần tạo bởi hai cung tròn có diện tích là 356,3 (cm2).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.