15 câu Trắc nghiệm Toán 10 Kết nối tri thức Hệ bất phương trình bậc nhất hai ẩn có đáp án
33 người thi tuần này 4.6 1.9 K lượt thi 15 câu hỏi 30 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 3
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 2
Đề kiểm tra Ôn tập chương 9 (có lời giải) -Đề 1
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 3
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 2
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 1
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Danh sách câu hỏi:
Câu 1
A. \(\left\{ \begin{array}{l}x + 3y \ge 0\\2x \le 0\end{array} \right.\)
B. \(\left\{ \begin{array}{l}{x^2} + 3y \ge 2\\2x + y \le - 1\end{array} \right.\)
C. \(\left\{ \begin{array}{l}4x + 3y - 1 \ge 0\\x + {y^3} > 0\end{array} \right.\)
D. \(\left\{ \begin{array}{l} - {x^2} + 3y \ge 5\\x + {y^3} \le 1\end{array} \right.\)
Lời giải
Đáp án đúng là: A
Các hệ bất phương trình \(\left\{ \begin{array}{l}{x^2} + 3y \ge 2\\2x + y \le - 1\end{array} \right.\); \(\left\{ \begin{array}{l}4x + 3y - 1 \ge 0\\x + {y^3} > 0\end{array} \right.\); \(\left\{ \begin{array}{l} - {x^2} + 3y \ge 5\\x + {y^3} \le 1\end{array} \right.\) đều chứa các bất phương trình bậc hai hoặc bậc ba như : x2 + 3y ≥ 2 ; x + y3 > 0 ; – x2 + 3y ≥ 5.
Do đó, các hệ bất phương trình \(\left\{ \begin{array}{l}{x^2} + 3y \ge 2\\2x + y \le - 1\end{array} \right.\); \(\left\{ \begin{array}{l}4x + 3y - 1 \ge 0\\x + {y^3} > 0\end{array} \right.\); \(\left\{ \begin{array}{l} - {x^2} + 3y \ge 5\\x + {y^3} \le 1\end{array} \right.\) không phải là hệ bất phương trình bậc nhất hai ẩn.
Hệ \(\left\{ \begin{array}{l}x + 3y \ge 0\\2x \le 0\end{array} \right.\) có hai bất phương trình x + 3y ≥ 0 và 2x ≤ 0 đều là các bất phương trình bậc nhất hai ẩn.
Vậy ta chọn đáp án A.
Câu 2
A. Điểm O(0 ; 0) thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} - x + 3y \ge 0\\2x \le 0\end{array} \right.\)
B. Điểm M(1 ; 0) thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} - x + 3y \ge 0\\2x \le 0\end{array} \right.\)
C. Điểm N(0 ; –1) thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} - x + 3y \ge 0\\2x \le 0\end{array} \right.\)
D. Điểm P(1 ; 1) thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} - x + 3y \ge 0\\2x \le 0\end{array} \right.\).
Lời giải
Đáp án đúng là: A
+ Vì –0 + 3.0 = 0 và 2.0 = 0 nên cặp số (0; 0) là nghiệm của cả hai bất phương trình –x + 3y ≥ 0 và 2x ≤ 0.
Suy ra điểm O(0; 0) thuộc miền nghiệm của hệ \(\left\{ \begin{array}{l} - x + 3y \ge 0\\2x \le 0\end{array} \right.\).
Vậy khẳng định A là đúng.
+ Vì –1 + 3.0 = –1 < 0 và 2. (–1) = –2 < 0 nên cặp số (1 ; 0) không là nghiệm của bất phương trình –x + 3y ≥ 0.
Suy ra điểm M(1 ; 0) không thuộc miền nghiệm của hệ \(\left\{ \begin{array}{l} - x + 3y \ge 0\\2x \le 0\end{array} \right.\).
Vậy khẳng định B là sai.
+ Vì –0 + 3. (–1) = –3 < 0 và 2. 0 = 0 nên cặp số (0; –1) không là nghiệm của bất phương trình –x + 3y ≥ 0.
Suy ra điểm N(0 ; –1) không thuộc miền nghiệm của hệ \(\left\{ \begin{array}{l} - x + 3y \ge 0\\2x \le 0\end{array} \right.\).
Vậy khẳng định C là sai.
+ Vì –1 + 3. 1 = 2 > 0 và 2. 1 = 2 > 0 nên cặp số (1; 1) không là nghiệm của bất phương trình 2x ≤ 0.
Suy ra điểm P(1; 1) không thuộc miền nghiệm của hệ \(\left\{ \begin{array}{l} - x + 3y \ge 0\\2x \le 0\end{array} \right.\).
Vậy khẳng định D là sai.
Vậy ta chọn đáp án A.
Câu 3
A. Hệ \(\left\{ \begin{array}{l}x + y \ge - 1\\{y^2} - 1 \le 0\end{array} \right.\) không phải là hệ bất phương trình bậc nhất hai ẩn;
B. Hệ \(\left\{ \begin{array}{l}x \ge 1 + y\\5x + y < 0\end{array} \right.\) là hệ bất phương trình bậc nhất hai ẩn;
C. Hệ \(\left\{ \begin{array}{l}x + 1 + y > 0\\{x^2} + y < 0\end{array} \right.\) là hệ bất phương trình bậc nhất hai ẩn;
D. Hệ \(\left\{ \begin{array}{l}\frac{1}{2}x + 2y < 7\\x + 3y \le 0\end{array} \right.\) là hệ bất phương trình bậc nhất hai ẩn;
Lời giải
Đáp án đúng là: C
+ Vì \(\left\{ \begin{array}{l}x + y \ge - 1\\{y^2} - 1 \le 0\end{array} \right.\) chứa bất phương trình bậc hai y2 – 1 ≤ 0 nên hệ này không phải là hệ bất phương trình bậc nhất hai ẩn.
Do đó khẳng định A đúng.
+ Vì \(\left\{ \begin{array}{l}x \ge 1 + y\\5x + y < 0\end{array} \right.\) chứa hai bất phương trình x ≥ 1 + y và 5x + y < 0 đều là các bất phương trình bậc nhất hai ẩn, nên hệ này là hệ bất phương trình bậc nhất hai ẩn.
Do đó khẳng định B đúng.
+ Vì \(\left\{ \begin{array}{l}x + 1 + y > 0\\{x^2} + y < 0\end{array} \right.\) chứa bất phương trình bậc hai x2
+ y < 0 nên hệ này không phải là hệ bất phương trình bậc nhất hai ẩn.Do đó khẳng định C sai.
+ Vì \(\left\{ \begin{array}{l}\frac{1}{2}x + 2y < 7\\x + 3y \le 0\end{array} \right.\)chứa hai bất phương trình \(\frac{1}{2}x + y < 7\) và x + 3y ≤ 0 đều là các bất phương trình bậc nhất hai ẩn nên hệ này là hệ bất phương trình bậc nhất hai ẩn.
Do đó khẳng định D đúng.
Vậy ta chọn đáp án C.
Câu 4
A. M(0; 1);
B. N(–1; 1);
. P(–1; 4);
D. Q(1; 3).
Lời giải
Đáp án đúng là: B
+ Ta có : –0 + 2.1 = 2 và 2.0 + 1 = 1 > –1.
Do đó cặp số (0; 1) không là nghiệm của bất phương trình 2x + y ≤ –1.
Vậy nên cặp số (0; 1) không là nghiệm của hệ bất phương trình\(\left\{ \begin{array}{l} - x + 2y \ge 2\\2x + y \le - 1\end{array} \right.\).
Suy ra điểm M(0; 1) không thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} - x + 2y \ge 2\\2x + y \le - 1\end{array} \right.\)
+ Ta có : –(–1) +2.1 = 3 > 2 và 2.(–1) + 1 = –1.
Do đó cặp số (–1; 1) là nghiệm của cả hai bất phương trình –x + 3y ≥2 và 2x + y ≤ –1.
Vậy nên, cặp số (–1; 1) là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} - x + 2y \ge 2\\2x + y \le - 1\end{array} \right.\).
Suy ra điểm N(–1; 1) thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} - x + 2y \ge 2\\2x + y \le - 1\end{array} \right.\).
+ Ta có : –(–1) + 2.4 = 9 > 2 và 2.(–1) + 4 = 2 > –1.
Do đó cặp số (–1; 4) không là nghiệm của bất phương trình 2x + y ≤ –1.
Vậy nên cặp số (–1; 4) không là nghiệm của hệ bất phương trình\(\left\{ \begin{array}{l} - x + 2y \ge 2\\2x + y \le - 1\end{array} \right.\).
Suy ra điểm P(–1; 4) không thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} - x + 2y \ge 2\\2x + y \le - 1\end{array} \right.\)
+ Ta có : –1 + 2.3 = 5 > 2 và 2.1 + 3 = 5 > –1.
Do đó cặp số (1; 3) không là nghiệm của bất phương trình 2x + y ≤ –1.
Vậy nên cặp số (1; 3) không là nghiệm của hệ bất phương trình\(\left\{ \begin{array}{l} - x + 2y \ge 2\\2x + y \le - 1\end{array} \right.\).
Suy ra điểm Q(1; 3) không thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} - x + 2y \ge 2\\2x + y \le - 1\end{array} \right.\)
Vậy điểm N(–1; 1) thuộc miền nghiệm của hệ bất phương trình đã cho nên ta chọn đáp án B.
Lời giải
Đáp án đúng là: C
+ Ta có : –3. (–1) + 2 = 5 > –2 và –1 + 2.2 = 3 > 1.
Do đó cặp số (–1 ; 2) không là nghiệm của bất phương trình x + 2y ≤ 1.
Vậy nên cặp số (–1 ; 2) không là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} - 3x + y > - 2\\x + 2y \le 1\end{array} \right.\).
Suy ra điểm M(–1 ; 2) không thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} - 3x + y > - 2\\x + 2y \le 1\end{array} \right.\).
+ Ta có : –3. 0 + (–1)= –1 > –2 và 0 + 2. (–1) = –2 < 1.
Do đó cặp số (0; –1) là nghiệm của cả hai bất phương trình –3x + y > –2 và x + 2y ≤ 1.
Vậy nên cặp số (0; –1) là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} - 3x + y > - 2\\x + 2y \le 1\end{array} \right.\).
Suy ra điểm M(0; –1) thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} - 3x + y > - 2\\x + 2y \le 1\end{array} \right.\).
+ Ta có : –3. 0 + 0 = 0 > –2 và 0 + 2.0 = 0 < 1.
Do đó cặp số (0 ; 0) là nghiệm của cả hai bất phương trình –3x + y > –2 và x + 2y ≤ 1.
Vậy nên cặp số (0 ; 0) là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} - 3x + y > - 2\\x + 2y \le 1\end{array} \right.\).
Suy ra điểm O(0 ; 0) thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} - 3x + y > - 2\\x + 2y \le 1\end{array} \right.\).
Vậy hai điểm M(0; –1) và O(0 ; 0) thuộc miền nghiệm của hệ \(\left\{ \begin{array}{l} - 3x + y > - 2\\x + 2y \le 1\end{array} \right.\).
Do đó ta chọn đáp án C.
Câu 6
B. \(\left\{ \begin{array}{l}2x - y > 0\\2x + y > 1\end{array} \right.\)
C. \(\left\{ \begin{array}{l} - x - 4y > - 3\\2x + y \le 2\end{array} \right.\)
D. \(\left\{ \begin{array}{l}2x - y \le - 3\\5y \ge - 1\end{array} \right.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Cả M và N đều không thuộc miền nghiệm của hệ đã cho.
B. Điểm M thuộc miền nghiệm còn N không thuộc miền nghiệm của hệ đã cho.
C. Điểm M không thuộc miền nghiệm còn N thuộc miền nghiệm của hệ đã cho.
D. Cả hai điểm M và N đều thuộc miền nghiệm của hệ đã cho.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
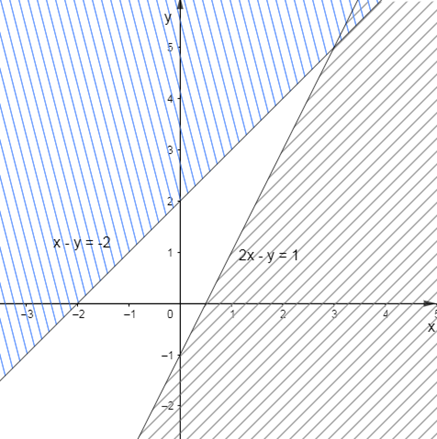
Câu 9
A. \(\left\{ \begin{array}{l}x - y \ge - 2\\2x - y \ge 1\end{array} \right.\)
B. \(\left\{ \begin{array}{l}x - y > - 2\\2x - y < 1\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x - y < - 2\\2x - y > 1\end{array} \right.\)
D. \(\left\{ \begin{array}{l}x - y < - 2\\2x - y < 1\end{array} \right.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. Fmin = \(\frac{{11}}{5}\);
B. Fmin = 0;
C. Fmin = 2;
D. Fmin = 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. (0; 0);
B. (\(\frac{2}{3}\); \(\frac{{ - 2}}{3}\));
C. (0; –1);
D. (1; 0).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 900\end{array} \right.\);
B. \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\2x + y \le 18\end{array} \right.\);
C. \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\2x + y > 18\end{array} \right.\);
D. \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + 2y \le 18\end{array} \right.\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A. – 1;
B. \(\frac{1}{5}\);
C. 2;
D. 1
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A. (0; 1) ∈ S;
B. (0; –1) ∉ S;
C. \(\left( {\frac{1}{3};1} \right)\) ∈ S;
D. \(\left( { - \frac{1}{3};1} \right)\) ∉ S.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A. 5 kg loại I và 1 kg loại II;
B. 5 kg loại I và 5 kg loại II;
C. 6 kg loại I và 0 kg loại II;
D. 0 kg loại I và 6 kg loại II;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.