Đề kiểm tra giữa kỳ 2 Toán 8 có đáp án ( Mới nhất)

$\{\begin{matrix} x + 1 \neq 0 \\ x - 2 \neq 0 \\ x^{2} - x - 2 \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x + 1 \neq 0 \\ x - 2 \neq 0 \\ x^{2} + x - 2 x - 2 \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x + 1 \neq 0 \\ x - 2 \neq 0 \\ (x + 1) (x - 2) \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x + 1 \neq 0 \\ x - 2 \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x \neq - 1 \\ x \neq 2 \end{matrix}$

Khi đó, ta có:

$B = \frac{2 x}{x + 1} + \frac{3}{x - 2} - \frac{2 x^{2} + 1}{x^{2} - x - 2} = \frac{2 x (x - 2)}{(x + 1) (x - 2)} + \frac{3 (x + 1)}{(x - 2) (x + 1)} - \frac{2 x^{2} + 1}{(x - 2) (x + 1)} = \frac{2 x^{2} - 4 x}{(x + 1) (x - 2)} + \frac{3 x + 3}{(x - 2) (x + 1)} - \frac{2 x^{2} + 1}{(x - 2) (x + 1)} = \frac{2 x^{2} - 4 x + 3 x + 3 - (2 x^{2} + 1)}{(x + 1) (x - 2)} = \frac{2 x^{2} - 4 x + 3 x + 3 - 2 x^{2} - 1}{(x + 1) (x - 2)} = \frac{2 x^{2} - 2 x^{2} - 4 x + 3 x + 3 - 1}{(x + 1) (x - 2)} = \frac{- x + 2}{(x + 1) (x - 2)} = \frac{- (x - 2)}{(x + 1) (x - 2)} = \frac{- 1}{x + 1}$

Vậy

B = \frac{- 1}{x + 1}

c) Ta có P = A.B nên:

$P = \frac{x + x^{2}}{2 - x} . \frac{- 1}{x + 1} = \frac{x (x + 1)}{2 - x} . \frac{- 1}{x + 1} = \frac{- x}{2 - x} = \frac{x}{x - 2} = 1 + \frac{2}{x - 2}$

Để biểu thức $P = 1 + \frac{2}{x - 2}$ đạt giá trị lớn nhất thì $\frac{2}{x - 2}$ đạt giá trị lớn nhất.

Suy ra (x – 2) đạt giá trị nhỏ nhất.

∙ Xét x – 2 < 0 hay x < 2 thì $\frac{2}{x - 2}$ < 0.

Do đó không xác định được giá trị nhỏ nhất trong trường hợp này.

∙ Xét x – 2 > 0 hay x > 2 thì $\frac{2}{x - 2}$ > 0.

Ta thấy: x là số nguyên lớn hơn 2 mà (x – 2) đạt giá trị nhỏ nhất nên x = 3.

Vậy để P = A . B đạt giá trị lớn nhất thì x = 3.

Câu 2

Giải phương trình

a) $\frac{x + 1}{3} + \frac{1}{2} = \frac{x - 1}{6} - 1$ ;

b) 4x² – 1 – x(2x – 1) = 0;

c) $\frac{x + 3}{x - 3} + \frac{x - 3}{x + 3} = \frac{x^{2} + 2 x}{x^{2} - 9} + 1$ ;
d) (x² + x – 1)(x² + x + 3) = 5.

Xem đáp án

Lời giải

a) $\frac{x + 1}{3} + \frac{1}{2} = \frac{x - 1}{6} - 1$

$\Leftrightarrow \frac{2 (x + 1)}{2.3} + \frac{3.1}{3.2} = \frac{x - 1}{6} - \frac{6}{6} \Leftrightarrow \frac{2 x + 2}{6} + \frac{3}{6} = \frac{x - 1}{6} - \frac{6}{6}$

Û 2x + 2 + 3 = x – 1 – 6

Û 2x + 5 = x – 7

Û 2x – x = – 7 – 5

Û x = – 12.

Vậy tập nghiệm của phương trình đã cho là S = {–12}.

b) 4x² – 1 – x(2x – 1) = 0

Û 4x² – 1 – 2x² + x = 0

Û 4x² – 2x² + x – 1 = 0

Û 2x² + x – 1 = 0

Û 2x² + 2x – x – 1 = 0

Û 2x(x + 1) – (x + 1) = 0

Û (x + 1)(2x – 1) = 0

$\Leftrightarrow [\begin{matrix} x + 1 = 0 \\ 2 x - 1 = 0 \end{matrix} \Leftrightarrow [\begin{matrix} x = - 1 \\ 2 x = 1 \end{matrix} \Leftrightarrow [\begin{matrix} x = - 1 \\ x = \frac{1}{2} \end{matrix}$

Vậy tập nghiệm của phương trình đã cho là

S = \{- 1; \frac{1}{2}\}

c) $\frac{x + 3}{x - 3} + \frac{x - 3}{x + 3} = \frac{x^{2} + 2 x}{x^{2} - 9} + 1$

Điều kiện xác định:

$\{\begin{matrix} x - 3 \neq 0 \\ x + 3 \neq 0 \\ x^{2} - 9 \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x - 3 \neq 0 \\ x + 3 \neq 0 \\ (x - 3) (x + 3) \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x - 3 \neq 0 \\ x + 3 \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x \neq 3 \\ x \neq - 3 \end{matrix}$

Khi đó phương trình đã cho tương đương với:

$\frac{x + 3}{x - 3} + \frac{x - 3}{x + 3} = \frac{x^{2} + 2 x}{(x + 3) (x - 3)} + 1 \Leftrightarrow \frac{(x + 3) (x + 3)}{(x - 3) (x + 3)} + \frac{(x - 3) (x - 3)}{(x - 3) (x + 3)} = \frac{x^{2} + 2 x}{(x - 3) (x + 3)} + \frac{(x - 3) (x + 3)}{(x - 3) (x + 3)} \Leftrightarrow \frac{{(x + 3)}^{2}}{(x - 3) (x + 3)} + \frac{{(x - 3)}^{2}}{(x - 3) (x + 3)} = \frac{x^{2} + 2 x}{(x - 3) (x + 3)} + \frac{x^{2} - 9}{(x - 3) (x + 3)}$

Þ (x + 3)² + (x – 3)² = x² + 2x + x² – 9

Û x² + 6x + 9 + x² – 6x + 9 = 2x² + 2x – 9

Û 2x² + 18 = 2x² + 2x – 9

Û 2x² + 2x – 2x² = 9 + 18

Û 2x = 27

Û x = $\frac{27}{2}$ (thỏa mãn)

Vậy tập nghiệm của phương trình là S =

\{\frac{27}{2}\}

;

d) (x² + x – 1)(x² + x + 3) = 5

Đặt t = x² + x.

Khi đó phương trình đã cho trở thành:

(t – 1)(t + 3) = 5

Û t² – t + 3t – 3 = 5

Û t² + 2t – 3 = 5

Û t² + 2t – 8 = 0

Û t² – 2t + 4t – 8 = 0

Û t(t – 2) + 4(t – 2) = 0

Û (t – 2)(t + 4) = 0

\Leftrightarrow [\begin{matrix} t - 2 = 0 \\ t + 4 = 0 \end{matrix} \Leftrightarrow [\begin{matrix} t = 2 \\ t = - 4 \end{matrix}

∙ Với t = 2, ta có: x² + x = 2

Û x² – x + 2x – 2 = 0

Û x(x – 1) + 2(x – 1) = 0

Û (x – 1)(x + 2) = 0

$\Leftrightarrow [\begin{matrix} x - 1 = 0 \\ x + 2 = 0 \end{matrix} \Leftrightarrow [\begin{matrix} x = 1 \\ x = - 2 \end{matrix}$

∙ Với t = –4, ta có: x² + x = –4

x² + x + 4 = 0

$x^{2} + x + \frac{1}{4} + \frac{15}{4} = 0 {(x + \frac{1}{2})}^{2} + \frac{15}{4} = 0$

Vì ${(x + \frac{1}{2})}^{2} \geq 0$ nên ${(x + \frac{1}{2})}^{2} + \frac{15}{4} > 0$

Do đó không có giá trị x thỏa mãn

{(x + \frac{1}{2})}^{2} + \frac{15}{4} = 0

Câu 3

Giải bài toán bằng cách lập phương trình

Một người đi xe máy từ A đến B với vận tốc 30 km/h. Khi đến B người đó nghỉ 30 phút rồi quay trở về A với vận tốc 40 km/h. Tính quãng đường AB biết thời gian cả đi, về và nghỉ là 5 giờ 10 phút ?

Xem đáp án

Lời giải

Gọi x (km) là độ dài quãng đường AB (x > 0).

Một người đi xe máy từ A đến B với vận tốc 30 km/h nên thời gian người đó từ A đến B là $\frac{x}{30}$ (h).

Người đó đi B về A với vận tốc 40 km/h nên thời gian để đi từ B về A là $\frac{x}{40}$ (h).

Thời gian người đó nghỉ là: 30 phút = $\frac{1}{2}$ h.

Đổi 5 giờ 10 phút = $\frac{31}{6}$ giờ.

Theo đề bài, tổng thời gian người đó đi, quay về và nghỉ là 5 giờ 10 phút nên ta có phương trình:

$\frac{x}{30} + \frac{x}{40} + \frac{1}{2} = \frac{31}{6} \Leftrightarrow \frac{x .4}{30.4} + \frac{x .3}{40.3} + \frac{1.60}{2.60} = \frac{31.20}{6.20} \Leftrightarrow \frac{4 x}{120} + \frac{3 x}{120} + \frac{60}{120} = \frac{620}{120}$

Û 4x + 3x + 60 = 620

Û 7x = 620 – 60

Û 7x = 560

Û x = 560 : 7

Û x = 80 (thỏa mãn điều kiện)

Vậy độ dài quãng đường AB là 80 km.

Câu 4

Cho tam giác ABC có AB = 5 cm; BC = 8 cm. Trên cạnh AB lấy điểm D sao cho AD = 2 cm. Qua D kẻ đường thẳng song song với BC cắt AC ở E và cắt đường thẳng qua C song song với AB ở F.

a) Tính DE.

b) BF cắt AC ở I. Tính $\frac{I F}{I B}$ .

c) Chứng minh rằng IC² = IE.IA.
d) BE cắt AF ở H. Tính $\frac{H A}{H F}$ .

Xem đáp án

Lời giải

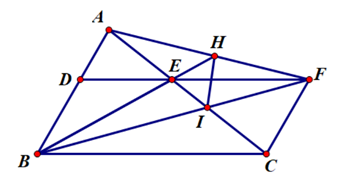
Cho tam giác ABC có AB = 5 cm; BC = 8 cm. Trên cạnh AB lấy điểm D sao cho AD = 2 cm. (ảnh 1)

a)Áp dụng định lý Ta-let trong ∆ABC có DE // BC, ta có:

$\frac{A D}{A B} = \frac{D E}{B C}$

$\Leftrightarrow D E = \frac{A D . B C}{A B} = \frac{2.8}{5} = 3, 2$ (cm).

b) Theo đề ta có DE // BC hay DF // BC và BD // CF.

Suy ra tứ giác BDFC là hình bình hành nên ta có FC = BD.

Mà BD = AB – AD = 5 – 2 = 3 (cm).

Suy ra FC = 3 cm.

Ta có CF // AD (gt), áp dụng hệ quả của định lý Ta-let, ta có:

$\frac{I F}{I B} = \frac{F C}{A D} = \frac{3}{5}$

c) Áp dụng hệ quả của định lý Ta – let với CF // AD, ta có:

$\frac{I F}{I B} = \frac{I C}{I A}$ (1)

Áp dụng hệ quả định lý Ta – let với EF // BC, ta có:

$\frac{I F}{I B} = \frac{I E}{I C}$ (2)

Từ (1) và (2) suy ra $\frac{I C}{I A} = \frac{I E}{I C} = \frac{I F}{I B}$ nên IC² = IE.IA.

Câu 5

a) Tìm giá trị nhỏ nhất của $Q = \frac{x^{2} - 4 x + 1}{x^{2}}$ .
b) Tìm $a, b, c \in ℕ $ : $(a - \frac{1}{b}) (b - \frac{1}{c}) (c - \frac{1}{a}) \in ℕ $ .

Xem đáp án

Lời giải

a) $Q = \frac{x^{2} - 4 x + 1}{x^{2}}$

Điều kiện xác định: x ≠ 0.

Ta có $Q = \frac{x^{2} - 4 x + 1}{x^{2}} = 1 - \frac{4}{x} + \frac{1}{x^{2}}$ .

Đặt $y = \frac{1}{x}$ . Khi đó:

Q = 1 – 4y + y² = y²– 4y + 4 – 3

= (y – 2)² – 3 ≥ – 3.

Vậy min Q = – 3 khi y – 2 = 0

\Leftrightarrow y = \frac{1}{x} = 2 \Leftrightarrow x = \frac{1}{2}

b) Ta có:

$(a - \frac{1}{b}) (b - \frac{1}{c}) (c - \frac{1}{a}) = (\frac{a b - 1}{b}) (\frac{b c - 1}{c}) (\frac{a c - 1}{a}) = \frac{(a b - 1) (b c - 1) (a c - 1)}{a . b . c} = \frac{(a b^{2} c - a b - b c + 1) (a c - 1)}{a . b . c} = \frac{a^{2} b^{2} c^{2} - a b^{2} c - a^{2} b c + a b - a b c^{2} + b c + a c + 1}{a . b . c} = a b c - a - b - c + \frac{1}{a} + \frac{1}{b} + \frac{1}{c} + \frac{1}{a . b . c} = a b c - (a + b + c) + (\frac{1}{a} + \frac{1}{b} + \frac{1}{c}) + \frac{1}{a . b . c}$

Để $(a - \frac{1}{b}) (b - \frac{1}{c}) (c - \frac{1}{a}) \in ℕ *$ thì a, b, c Î $ℕ *$ và a.b.c Î Ư(1) = {1}.

Với a = b = c = 1

Ta thay vào:

$a b c - (a + b + c) + (\frac{1}{a} + \frac{1}{b} + \frac{1}{c}) + \frac{1}{a . b . c} = 1.1.1 - (1 + 1 + 1) + (1 + 1 + 1) + 1 = 2$

Vậy a = b = c = 1.

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Giáo dục công dân

Tin học

Tiếng Anh

Giáo dục Kinh tế và Pháp luật

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Tin học

Giáo dục Kinh tế và Pháp luật

Global success

iLearn Smart World

Friends Global

Explore new worlds

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học