Đề kiểm tra giữa kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề số 14
27 người thi tuần này 4.6 10.3 K lượt thi 5 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 10
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 09
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 08
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 07
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 06
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 05
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 04
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 03
Danh sách câu hỏi:
Lời giải
a) Thay x = 3 (TMĐK) vào biểu thức , ta được:
Vậy khi x = 3 thì giá trị biểu thức A = 3.b) Với điều kiện x ≠ ±2, ta có:
(với x ≠ ±2)
c) Ta có:
Mà A.B = 1 nên
Þ 2x = (x – 1)(x + 2) (vì x ≠ 1; x ≠ ±2)
Û 2x = x2 + 2x – x – 2
Û 2x = x2 + x – 2
Û x2 + x – 2 – 2x = 0
Û x(x + 1) – 2 (1 + x) = 0
Û (x + 1)(x – 2) = 0
Đối chiếu với điều kiện x ≠ 1; x ≠ ±2, ta thấy chỉ có x = – 1 thỏa mãn.
Vậy để A.B = 1 thì x = – 1.
Lời giải
a) 3(x – 1) – 7 = 5(x + 2)
Û 3x – 3 – 7 = 5x + 10
Û 5x – 3x = – 3 – 7 – 10
Û 2x = – 20
Û x = (– 20) : 2
Û x = – 10
Vậy tập nghiệm của phương trình đã cho là S = {–10};b)
Û 15x + 5 – (2x + 6) = x + 20
Û 15x + 5 – 2x – 6 = x + 20
Û 15x – 2x – x = 20 – 5 + 6
Û 12x = 21
Vậy tập nghiệm của phương trình là S = ;
c)
Điều kiện xác định của phương trình:
Khi đó phương trình đã cho tương đương với:
Þ x2 – 3x + 2 – (x2 + x) = x – 8
Û x2 – 3x + 2 – x2 – x = x – 8
Û x2 – x2 – 3x– x – x = – 8 – 2
Û – 5x = – 10
Û 5x = 10
Û x = 10 : 5
Û x = 2 (thõa mãn điều kiện)
Vậy tập nghiệm của phương trình đã cho là S ={2}.Lời giải
Gọi x (km) là độ dài quãng đường từ A đến B (x > 0).
Vì ban đầu người đó dự định đi từ A đến B với vận tốc 60 km/h nên thời gian dự định đi hết quãng đường này là (h).
Trên thực tế người đó đã tăng tốc thêm 20 km/h nên vận tốc thực tế người đó đi từ A đến B là 60 + 20 = 80 (km/h).
Suy ra thời gian người đó đi hết quãng đường AB trên thực tế là (h).
Đổi 30 phút = giờ.
Vì trên thực tế người đó đến sớm hơn dự định ban đầu 30 phút nên ta có phương trình:
Û 4x – 120 = 3x
Û 4x – 3x = 120
Û x = 120 (thỏa mãn điều kiện)
Vậy độ dài quãng đường AB là 120 km.Lời giải
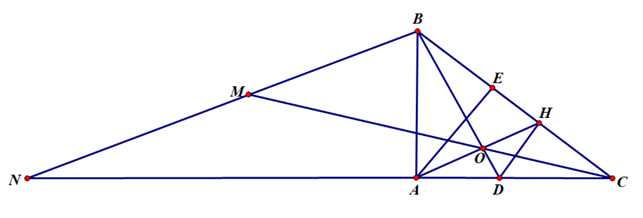
a) Ta có ∆ABC vuông tại A nên ta có:
AB2 + AC2 = BC2 ( định lý Py – ta – go)
Þ AC2 = BC2 – AB2 = 52 – 32 = 25 – 9 = 16
Þ AC = 4 (cm).
Xét ∆ABC có BD là tia phân giác của (D Î AC)
Ta có: (định lý)
Mà DC = BC – AD = 5 – AD
Þ 5.AD = 3.(5 – AD)
Û 5AD = 15 – 3AD
Û 8AD = 15
Û AD = = 1,875 (cm)
Vậy độ dài đoạn AC là 4 cm và AD là 1,875 cm.b) Theo đề ∆ABC vuông tại A nên có ;
DH vuông góc với BC tại H nên ;
Do đó .
Xét ∆ABC và ∆HDC có:
chung (giả thiết)
(cmt)
Suy ra, ∆ABC ∆HDC (g.g)
Vì ∆ABC ∆HDC (cmt) nên (các cạnh tương ứng tỉ lệ)
Þ CH.CB = CA.CD.c) Vì E là hình chiếu của A trên BC nên (E Î BC).
DH vuông góc với BC tại H (H Î BC).
Suy ra DH // AE (định lý)
Áp dụng định lý Ta – let trong ∆AEC có DH // AE (cmt)
Ta có: (1);
Xét ∆ABC có BD là tia phân giác của (D Î AC)
Ta có: (2);
Từ (1) và (2) suy ra .Lời giải
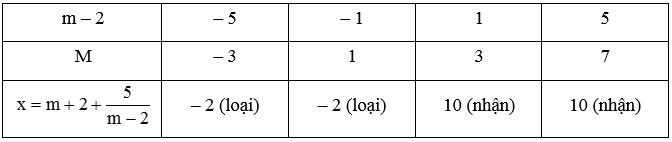
Điều kiện xác định của phương trình là:
x – m ≠ 0 suy ra x ≠ m.
Ta có:
Þ mx – m2 = 2x + 1
Û mx – 2x = m2 + 1
Û x(m – 2) = m2 + 1
Nghiệm của phương trình đã cho với m – 2 ≠ 0 Û m ≠ 2
Để x Î N khi đó m – 2 Î Ư(5) = { ± 1; ± 5} và