Bộ 10 đề thi giữa kì 2 Toán 10 Kết nối tri thức có đáp án - Đề 10
25 người thi tuần này 4.6 271 lượt thi 24 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Câu 1
Cho đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ sau:
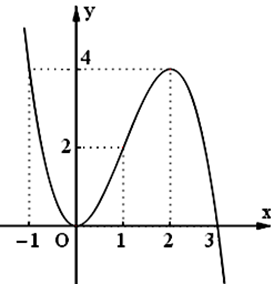
Hàm số \(y = f\left( x \right)\) nghịch biến trên khoảng
A. \(\left( {2;\,\,3} \right)\);
B. \(\left( {1;\,\,3} \right)\);
C. \(\left( {0;\,\,2} \right)\);
D. \(\left( { - 1;\,\,1} \right)\).
Lời giải
Đáp án đúng là: A
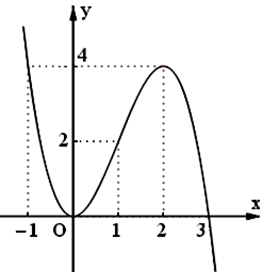
Từ hình vẽ, ta thấy đồ thị hàm số \(y = f\left( x \right)\) đi xuống từ trái sang phải trên khoảng \(\left( {2;\,\,3} \right)\) nên hàm số \(y = f\left( x \right)\) nghịch biến trên khoảng \(\left( {2;\,\,3} \right)\).
Câu 2
A. 3;
B. 1;
C. 0;
D. – 3.
Lời giải
Đáp án đúng là: B
Thay \(x = 1\) vào hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + 3\) ta được: \(f\left( 1 \right) = {1^3} - {3.1^2} + 3 = 1\).
Câu 3
A. \(\mathbb{R}\backslash \left\{ { - 1;\,\,6} \right\}\);
B. \(\left( { - \infty ;\,\,5} \right)\);
C. \(\left( { - \infty ;\,\,5} \right]\backslash \left\{ { - 1} \right\}\);
D. \(\left( {\infty ;\,\,5} \right)\backslash \left\{ { - 1;\,\,6} \right\}\).
Lời giải
Đáp án đúng là: C
Điều kiện xác định của hàm số \(y = \frac{{\sqrt {5 - x} }}{{{x^2} - 5x - 6}}\) là \(\left\{ \begin{array}{l}5 - x \ge 0\\{x^2} - 5x - 6 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 5\\x \ne 6\\x \ne - 1\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \le 5\\x \ne - 1\end{array} \right.\).
Vậy tập xác định của hàm số là \(D = \left( { - \infty ;\,5} \right]\backslash \left\{ { - 1} \right\}\).
Câu 4
A. \(x = - 3\);
B. \(x = \frac{3}{2}\);
C. \(x = - \frac{3}{2}\);
D. \(x = 3\).
Lời giải
Đáp án đúng là: C
Parabol \(y = - 2{x^2} - 6x + 3\) có hoành độ đỉnh là \(x = - \frac{b}{{2a}} = - \frac{{ - 6}}{{2.\left( { - 2} \right)}} = - \frac{3}{2}\).
Câu 5
A. \(\left( { - \infty ; - \frac{b}{{2a}}} \right)\);
B. \(\left( { - \frac{b}{{2a}}; + \infty } \right)\);
C. \(\left( { - \frac{\Delta }{{4a}};\, + \infty } \right)\);
D. \(\left( { - \infty ; - \frac{\Delta }{{4a}}} \right)\).
Lời giải
Đáp án đúng là: B
Với \(a > 0\) ta có bảng biến thiên:
|
\(x\) |
\( - \infty \) \( - \frac{b}{{2a}}\) \( + \infty \) |
|
\(y\) |
\( + \infty \) \( - \infty \)
\( - \frac{\Delta }{{4a}}\) |
Hàm số bậc hai \(y = a{x^2} + bc + c\,\,\left( {a > 0} \right)\) có biệt thức \(\Delta = {b^2} - 4ac\) đồng biến trên khoảng \(\left( { - \frac{b}{{2a}}; + \infty } \right)\).
Câu 6
Cho parabol \(\left( P \right):y = {x^2} + bx + 1\) đi qua điểm \(A\left( { - 1;\,\,3} \right)\). Khi đó
A. \(b = - 1\);
B. \(b = 1\);
C. \(b = 3\);
D. \(b = 2\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(f\left( x \right) = 3{x^2} - 4x + 4 - 3{x^2}\);
B. \(f\left( x \right) = {x^2} + x + 6\);
C. \(f\left( x \right) = {x^2} - 2{x^2} + 2\);
D. \(f\left( x \right) = {3^2}{x^2} + 3x + 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. \(f\left( x \right) = 0 \Leftrightarrow x = - 1\);
B. \(f\left( x \right) < 0 \Leftrightarrow x \in \left( { - \infty ;\,1} \right)\);
C. \(f\left( x \right) > 0 \Leftrightarrow x \in \left( {0;\,\,1} \right)\);
D. \(f\left( x \right) > 0 \Leftrightarrow x \in \left( { - \infty ;\, + \infty } \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. 2;
B. 0;
C. 1;
D. 3.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. Phương trình vô nghiệm;
B. Phương trình có một nghiệm;
C. Tổng các nghiệm của phương trình là \(\frac{5}{2}\);
D. Phương trình có hai nghiệm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Tổng các bình phương các nghiệm của phương trình \[\sqrt { - {x^2} + 2x + 3} = \sqrt {{x^2} - 4x + 3} \] bằng
A. 0;
B. 4;
C. Không tồn tại;
D. 9.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. \[\left( {6;\,\, - 10} \right)\];
B. \(\left( {3;\,\, - 5} \right)\);
C. \(\left( { - \frac{1}{2};\,\,3} \right)\);
D. \(\left( {3;\,\frac{1}{2}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
Phương trình đường thẳng đi qua hai điểm \(A\left( { - 2;\, - 6} \right)\) và \(B\left( { - 9;\,2} \right)\) là
A. \(8x - 7y + 58 = 0\) ;
B. \(8x + 7y + 58 = 0\);
C. \( - 7x + 8y + 34 = 0\);
D. \( - 7x + 8y = 0\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A. \(\left\{ \begin{array}{l}x = - 2t\\y = 2 - 5t\end{array} \right.\);
B. \(\left\{ \begin{array}{l}x = 2 + 2t\\y = - 3 - 5t\end{array} \right.\);
C. \(\left\{ \begin{array}{l}x = 2 + 2t\\y = 3 - 5t\end{array} \right.\);
D. \(\left\{ \begin{array}{l}x = 1 + 2t\\y = - 4 + 5t\end{array} \right.\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A. Hai đường thẳng \({d_1}\) và \({d_2}\) song song với nhau;
B. Hai đường thẳng \({d_1}\) và \({d_2}\) cắt nhau nhưng không vuông góc;
C. Hai đường thẳng \({d_1}\) và \({d_2}\) vuông góc với nhau;
D. Hai đường thẳng \({d_1}\) và \({d_2}\) trùng nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
Trong mặt phẳng tọa độ \(Oxy\), khoảng cách từ điểm \(A\left( {1;\,\, - 5} \right)\) đến đường thẳng \(d:x - 2y + 9 = 0\) là
A. 4;
B. \(4\sqrt 5 \);
C. 0;
D. \(\frac{{10\sqrt {26} }}{{13}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
A. \(\frac{1}{{\sqrt {10} }}\);
B. \(\frac{2}{{\sqrt {10} }}\);
C. \(\frac{3}{{\sqrt {10} }}\);
D. \(\frac{4}{{\sqrt {10} }}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
A. \(\left( {\frac{3}{2};\,\,\frac{3}{2}} \right)\);
B. \(\left( {1;\,\,1} \right)\);
C. \(\left( {2;\,\,2} \right)\);
D. \(\left( { - \frac{3}{2};\,\, - \frac{3}{2}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A. \(I\left( {4;\, - 6} \right),\,\,R = 4\);
B. \(I\left( { - 2;\,3} \right),\,\,R = 16\);
C. \(I\left( { - 4;\,6} \right),\,\,R = 4\);
D. \(I\left( { - 2;\,3} \right),\,\,R = 4\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
A. \({x^2} + {y^2} + 6x + 10y + 18 = 0\);
B. \({x^2} + {y^2} - 6x + 10y + 18 = 0\);
C. \({x^2} + {y^2} + 6x + 10y - 18 = 0\);
D. \({x^2} + {y^2} - 6x - 10y + 18 = 0\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
A. \(x + 7y - 1 = 0\);
B. \(x - 7y - 1 = 0\);
C. \(\frac{1}{4}x - \frac{7}{4}y - 1 = 0\);
D. \(x - 7y = 0\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập