Đề kiểm tra Bài tập cuối chương IV (có lời giải) - Đề 1
56 người thi tuần này 4.6 679 lượt thi 22 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 3
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 2
Đề kiểm tra Ôn tập chương 9 (có lời giải) -Đề 1
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 3
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 2
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 1
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Danh sách câu hỏi:
Câu 1
Lời giải
Chọn D
Ta có \(\overrightarrow a = - \overrightarrow b \). Do đó, \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương, cùng độ dài và ngược hướng nhau.
Câu 2
Lời giải
Chọn A
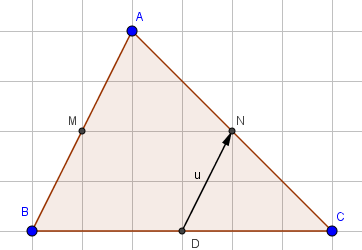
Nhìn hình ta thấy vectơ đối của vectơ \[\overrightarrow {DN} \] là:\[\overrightarrow {AM} ,{\rm{ }}\overrightarrow {MB} ,{\rm{ }}\overrightarrow {ND} \].
Câu 3
Lời giải
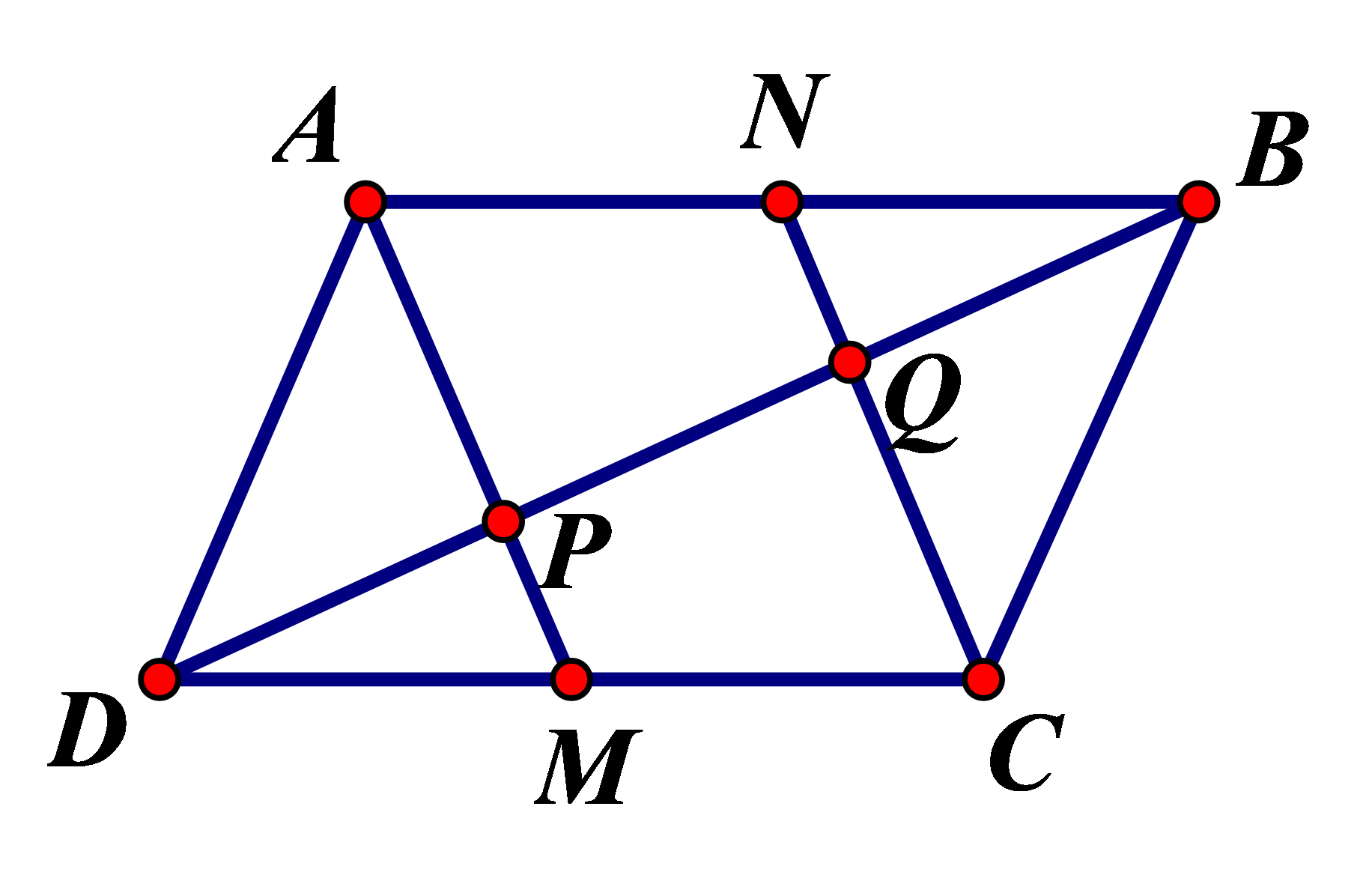
Chọn C
Ta có tứ giác \(DMBN\) là hình bình hành vì \(DM = NB = \frac{1}{2}AB,\,\,DM//NB\). Suy ra \(\overrightarrow {DM} = \overrightarrow {NB} \).
Xét tam giác \(CDQ\) có \(M\) là trung điểm của \(DC\) và \(MP//QC\) do đó \(P\) là trung điểm của \(DQ\). Tương tự xét tam giác \(ABP\) suy ra được \(Q\) là trung điểm của \(PB\)
Vì vậy \(DP = PQ = QB\) từ đó suy ra \(\overrightarrow {DP} = \overrightarrow {PQ} = \overrightarrow {QB} \).
Câu 4
Lời giải
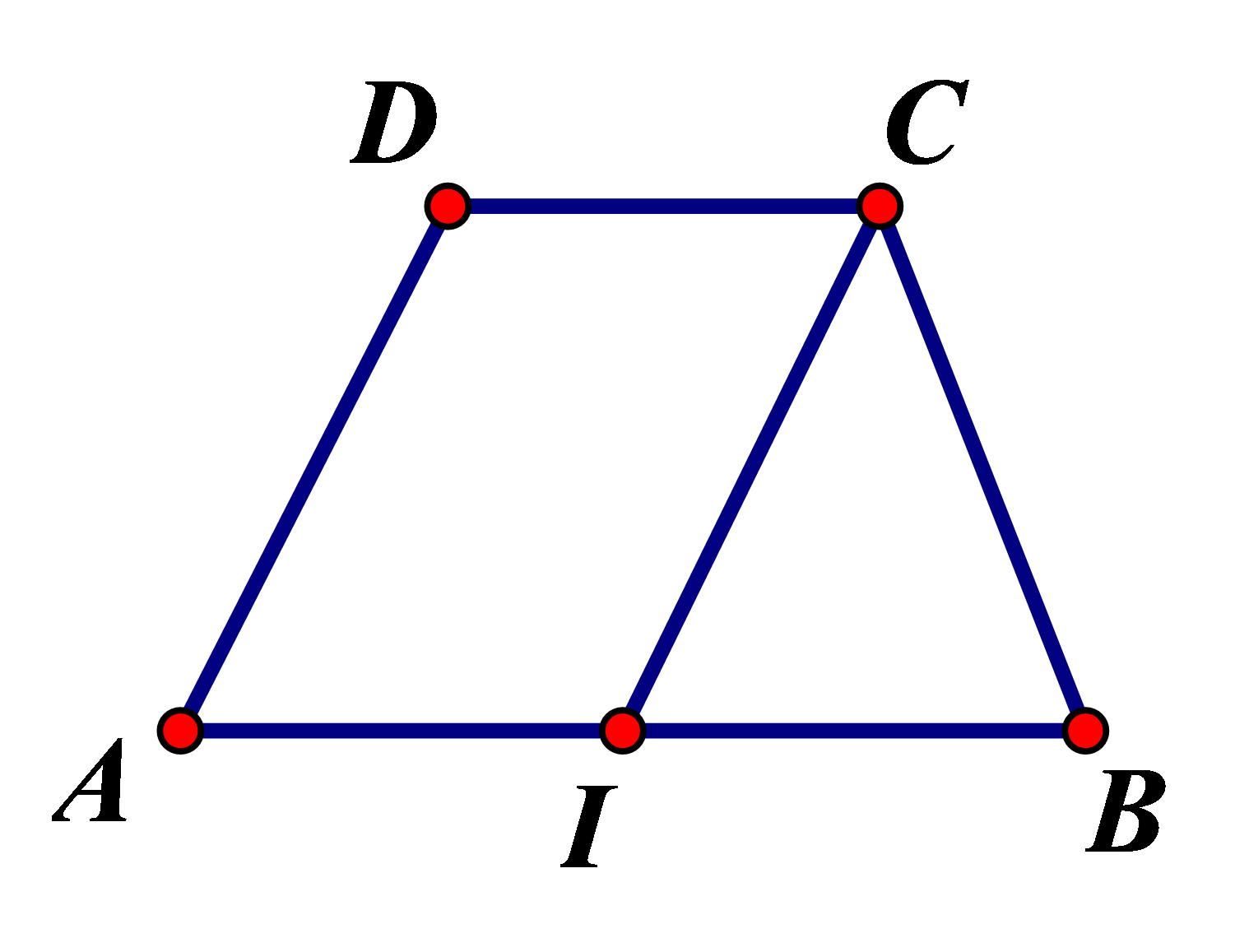
Chọn C
Ta có \[\overrightarrow {CI} = \overrightarrow {DA} \] suy ra \(AICD\) là hình bình hành
\( \Rightarrow \overrightarrow {AD} = \overrightarrow {IC} \)
Ta có \(DC = AI\) mà \(AB = 2CD\) do đó \(AI = \frac{1}{2}AB \Rightarrow \)\(I\)là trung điểm \(AB\)
Ta có \(DC = IB\) và \[DC//IB \Rightarrow \]tứ giác \(BCDI\) là hình bình hành
Suy ra \[\overrightarrow {DI} = \overrightarrow {CB} \]
Câu 5
Lời giải
Chọn B

Ta có \(AH \bot BC\) và \(DC \bot BC\) (do góc \(\widehat {DCB}\) chắn nửa đường tròn). Suy ra \(AH\parallel DC.\)
Tương tự ta cũng có \(CH\parallel AD.\)
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.