Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)

$\{\begin{matrix} x - 2 \neq 0 \\ x + 2 \neq 0 \\ x \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x \neq 2 \\ x \neq - 2 \\ x \neq 0 \end{matrix}$

Suy ra:

$P = (\frac{x - 1}{x (x - 2)} + \frac{x + 1}{x (x + 2)} - \frac{4}{x (x - 2) (x + 2)}) : (1 - \frac{2}{x})$

$= (\frac{x - 1}{x (x - 2)} + \frac{x + 1}{x (x + 2)} - \frac{4}{x (x - 2) (x + 2)}) : (\frac{x - 2}{x})$

$= (\frac{x - 1}{x (x - 2)} + \frac{x + 1}{x (x + 2)} - \frac{4}{x (x - 2) (x + 2)}) . (\frac{x}{x - 2})$

$= \frac{x - 1}{{(x - 2)}^{2}} + \frac{x + 1}{(x - 2) (x + 2)} - \frac{4}{{(x - 2)}^{2} (x + 2)}$

$= \frac{(x - 1) (x + 2)}{{(x - 2)}^{2} (x + 2)} + \frac{(x + 1) (x - 2)}{{(x - 2)}^{2} (x + 2)} - \frac{4}{{(x - 2)}^{2} (x + 2)}$

$= \frac{x^{2} - x + 2 x - 2}{{(x - 2)}^{2} (x + 2)} + \frac{x^{2} + x - 2 x - 2}{{(x - 2)}^{2} (x + 2)} - \frac{4}{{(x - 2)}^{2} (x + 2)}$

$= \frac{x^{2} - x + 2 x - 2 + x^{2} + x - 2 x - 2 - 4}{{(x - 2)}^{2} (x + 2)}$

$= \frac{2 x^{2} - 8}{{(x - 2)}^{2} (x + 2)} = \frac{2 (x^{2} - 4)}{{(x - 2)}^{2} (x + 2)}$

$= \frac{2 (x - 2) (x + 2)}{{(x - 2)}^{2} (x + 2)} = \frac{2}{x - 2}$

b) Xét phương trình |2x - 1| = 5 ⇔ $[\begin{matrix} 2 x - 1 = 5 \\ 2 x - 1 = - 5 \end{matrix} \Leftrightarrow [\begin{matrix} 2 x = 6 \\ 2 x = - 4 \end{matrix} \Leftrightarrow [\begin{matrix} x = 3 \\ x = - 2 \end{matrix}$

Đối chiếu ĐKXĐ ta suy ra được x = 3 là nghiệm của phương trình trên.

Thay x = 3 (TMĐK) vào biểu thức P, ta được:

$P = \frac{2}{3 - 2} = \frac{2}{1} = 2.$

Vậy với x thỏa mãn điều kiện |2x - 1| = 5 thì P = 2.

Câu 2

Giải các phương trình và bất phương trình sau:

a) $\frac{2 x + 1}{2 x^{2} + 5 x + 2} - \frac{3}{x^{2} - 4} = 2;$

b) |x - 3| - |x² - x + 1| = 1;

c) (x² - 1)(x³ + 1) ³ 0.

Xem đáp án

Lời giải

a) $\frac{2 x + 1}{2 x^{2} + 5 x + 2} - \frac{3}{x^{2} - 4} = 2$

$\Leftrightarrow \frac{2 x + 1}{2 x^{2} + 4 x + x + 2} - \frac{3}{x^{2} - 4} = 2$

$\Leftrightarrow \frac{2 x + 1}{2 x (x + 2) + (x + 2)} - \frac{3}{(x - 2) (x + 2)} = 2$

$\Leftrightarrow \frac{2 x + 1}{(2 x + 1) (x + 2)} - \frac{3}{(x - 2) (x + 2)} = 2$

ĐKXĐ:

$\{\begin{matrix} 2 x + 1 \neq 0 \\ x + 2 \neq 0 \\ x - 2 \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x \neq \frac{- 1}{2} \\ x \neq - 2 \\ x \neq 2 \end{matrix}$

Phương trình (1) trở thành

$\frac{1}{x + 2} - \frac{3}{(x - 2) (x + 2)} = 2$

$\Leftrightarrow \frac{x - 2}{(x - 2) (x + 2)} - \frac{3}{(x - 2) (x + 2)} = 2$

$\Leftrightarrow \frac{x - 5}{(x - 2) (x + 2)} = 2$

$\Leftrightarrow \frac{x - 5}{x^{2} - 4} = 2$

Û x - 5 = 2(x² - 4)

Û 2x² - x - 3 = 0

Û 2x² + 2x - 3x - 3 = 0

Û 2x(x + 1) - 3(x + 1) = 0

Û (2x - 3)(x + 1) = 0

$\Rightarrow [\begin{matrix} 2 x - 3 = 0 \\ x + 1 = 0 \end{matrix} \Leftrightarrow [\begin{matrix} x = \frac{3}{2} \\ x = - 1 \end{matrix}$

Đối chiếu ĐKXĐ suy ra tập nghiệm của phương trình là $S = \{- 1; \frac{3}{2}\} .$

b) |x - 3| - |x² - x + 1| = 1

Ta có:

$x^{2} - x + 1 = (x^{2} - x + \frac{1}{4}) + \frac{3}{4}$

$= {(x - \frac{1}{2})}^{2} + \frac{3}{4} > 0 \forall x$

Nên suy ra

|x - 3| - |x² - x + 1| = 1

Û |x - 3| - (x² - x + 1) = 1

Û |x - 3| = x² - x + 2 (2)

+) TH1: x ³ 3

Phương trình (2) trở thành

Û x - 3 = x² - x + 2

Û x² - 2x + 5 = 0

Mà do x² - 2x + 5 = (x² - 2x + 1) + 4

= (x - 1)² + 4 > 0 "x

Nên suy ra TH1 không cho nghiệm của x

+) TH2: x £ 3

Phương trình (2) trở thành

Û 3 - x = x² - x + 2

Û x² = 1

Đối chiếu ĐKXĐ nên suy ra x = ± 1 là nghiệm của phương trình.

c) (x² - 1)(x³ + 1) ³ 0

Û (x - 1)(x + 1)(x + 1)(x² - x + 1) ³ 0

Û (x - 1)(x + 1)²(x² - x + 1) ³ 0 (3)

Do:

+) (x + 1)² ³ 0 "x

+) $x^{2} - x + 1 = (x^{2} - x + \frac{1}{4}) + \frac{3}{4}$

$= {(x - \frac{1}{2})}^{2} + \frac{3}{4} > 0 \forall x$

Nên suy ra bất phương trình (3) trở thành

Û x - 1 ³ 0 Û x ³ 1

Vậy tập nghiệm của bất phương trình là S = {x | x ³ 1}.

Câu 3

Một người lái ô tô dự định đi từ địa điểm A đến địa điểm B với vận tốc 48 km/h. Nhưng thực tế, sau khi đi được 1 giờ với vận tốc dự định, ô tô nghỉ trong 10 phút. Do đó để kịp đến B đúng thời gian dự định, người đó phải tăng vận tốc thêm 6 km/h trên quãng đường còn lại. Tính quãng đường AB.

b) Kích thước một bể bơi được cho trên hình vẽ (mặt nước có dạng hình chữ nhật). Hãy tính xem bể chứa được bao nhiêu mét khối nước khi nó đầy ắp nước (coi thành bể có độ dày không đáng kể; làm tròn kết quả đến hàng phần trăm).

Xem đáp án

Lời giải

a) Gọi x (km) là độ dài quãng đường AB

+) Theo dự định, người đó đi từ A đến B với vận tốc 48 km/h với thời gian là $\frac{x}{48} h$

+) Thực tế, sau khi đi 1 giờ với vận tốc 48 km/h, người đó đi được quãng đường dài:

48.1 = 48 (km)

Vậy số quãng đường còn lại là x - 48 (km)

Sau khi nghỉ 10 phút, tức là $\frac{10}{60} = \frac{1}{6} h$ , để đến B đúng thời gian dự định thì người đó phải tăng vận tốc thêm 6 km/h trên quãng đường còn lại hết $\frac{x - 48}{48 + 6} = \frac{x - 48}{54} h$

Vậy trên thực tế người đó đến B đúng thời gian dự định nên suy ra ta có phương trình

$1 + \frac{1}{6} + \frac{x - 48}{54} = \frac{x}{48}$

$\Leftrightarrow \frac{x}{48} - \frac{x - 48}{54} = \frac{7}{6}$

$\Leftrightarrow \frac{9 x}{432} - \frac{8 (x - 48)}{432} = \frac{7}{6}$

$\Leftrightarrow \frac{9 x - 8 x + 384}{432} = \frac{7}{6}$

$\Leftrightarrow \frac{x + 384}{432} = \frac{7}{6}$

$\Leftrightarrow x + 384 = \frac{7}{6} .432 = 504$

Û x = 504 - 384 = 120

Vậy quãng đường AB có độ dài là 120 km.

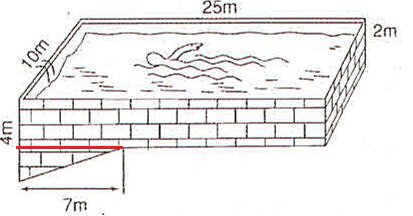
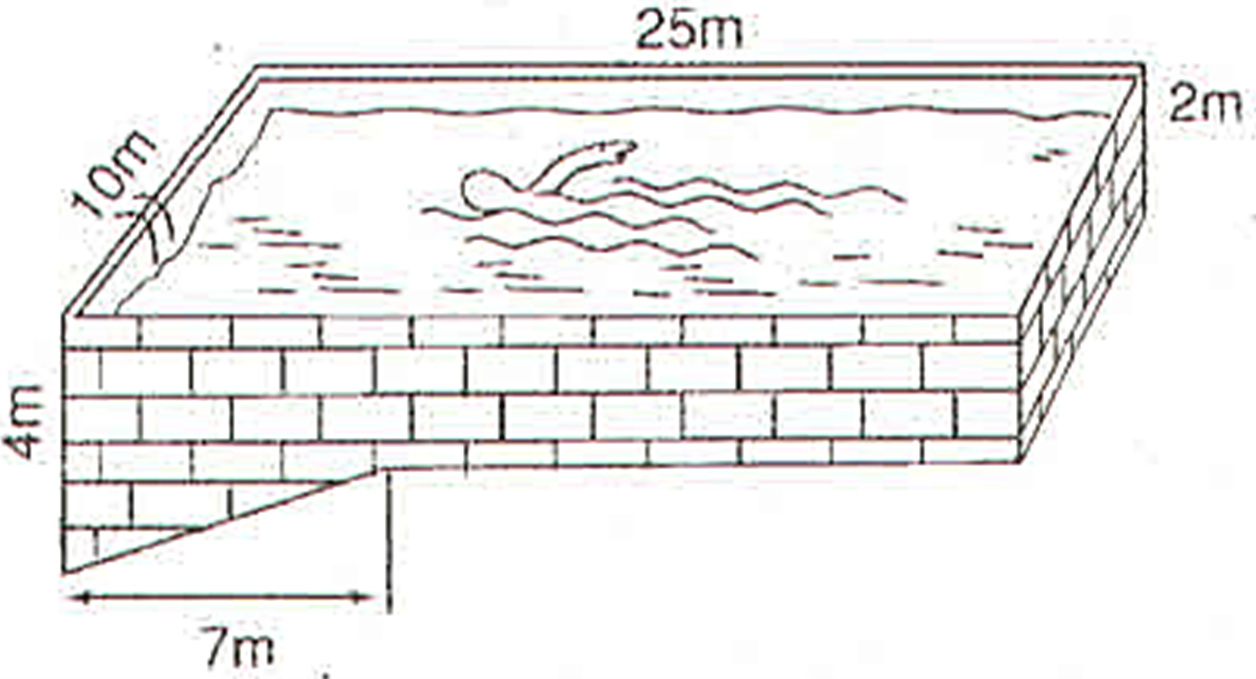
Media VietJack

Dựa vào hình vẽ ta thấy Bể bơi được chia thành hai phần:

+) Phần hình hộp chữ nhật với các kích thước là 10 m, 25 m, 2 m

+) Phần hình lăng trụ đứng với đáy là tam giác vuông có hai cạnh góc vuông là 4 - 2 = 2 m, 7 m và có chiều cao 10 m

Ta tính được:

+) Thể tích hình hộp chữ nhật là :

V_hhcn = 10.25.2 = 500 (m³)

+) Thể tích lăng trụ đứng tam giác :

$V_{l t} = S . h = (\frac{1}{2} .2.7) .10 = 70 (m^{3})$

Vậy thể tích bể bơi khi đầy ắp nước là

V = V_hhcn + V_lt = 500 + 70 = 570 (m³).

Câu 4

Cho tam giác ABC vuông tại A (AB < AC) và các điểm D, E, F lần lượt là trung điểm của các cạnh BC, AB, AC. Lấy điểm M thuộc đoạn EB (M khác E và B). Kẻ đường thẳng qua D vuông góc với MD tại D, đường thẳng này cắt AC tại N.

a) Chứng minh tam giác DEM đồng dạng tam giác DFN.

b) Chứng minh tam giác DMN đồng dạng tam giác ACB.

c) Chứng minh MN² = BM² + CN².

Xem đáp án

Lời giải

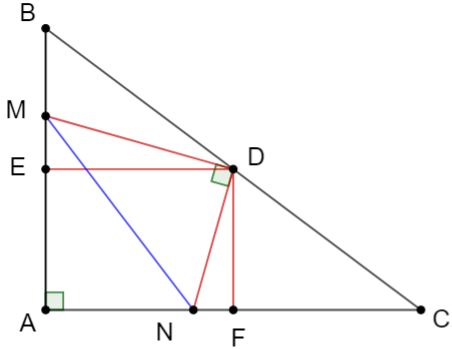
Media VietJack

a) +) Xét tam giác BAC có E, D lần lượt là trung điểm của BA và BC nên suy ra ED là đường trung bình của tam giác BAC

Þ ED // AC và $E D = \frac{A C}{2}; B E = \frac{A B}{2}$

Mà BA ^ AC nên suy ra BA ^ ED

Suy ra $\hat{M E D} = 90 °$

+) Xét tam giác CBA có F, D lần lượt là trung điểm của CA và CB nên suy ra FD là đường trung bình của tam giác BAC

Þ FD // AB và $F D = \frac{A B}{2}; C F = \frac{A C}{2}$

Mà BA ^ AC nên suy ra AC ^ FD

Suy ra $\hat{N F D} = 90 °$

+) Ta có:

ED // AC, FD // AB mà BA ^ AC nên suy ra ED ^ FD

$\Rightarrow \hat{E D N} + \hat{N D F} = 90 °$ (1)

Mà $\hat{M D N} = \hat{M D E} + \hat{E D N} = 90 °$ (2)

Từ (1) và (2) nên suy ra $\hat{M D E} = \hat{N D F}$ (Do cùng phụ với góc $\hat{E D N}$ )

Xét hai tam giác DDEM và DDFN có:

$\begin{matrix} \hat{M D E} = \hat{N D F} (c m t) \\ \hat{M E D} = \hat{N F D} (= 90 °) \end{matrix}\}$ ⇒ ∆DEM ᔕ DDFN (g – g)

b) Do DDEM ᔕ DDFN (g – g)

$\Rightarrow \frac{D M}{D N} = \frac{D E}{D F} = \frac{\frac{A C}{2}}{\frac{A B}{2}} = \frac{A C}{A B}$

$\Leftrightarrow \frac{D M}{A C} = \frac{D N}{A B}$

Xét hai tam giác DDMN và DACB có:

$\begin{matrix} \frac{D M}{A C} = \frac{D N}{A B} (c m t) \\ \hat{M D N} = \hat{C A B} (= 90 °) \end{matrix}\}$ ⇒ ∆DMN ᔕ DACB (c – g – c)

c) +) Ta có:

MN² = AM² + AN² = (AB - BM)² + (AC - CN)²

= AB² - 2AB.BM + BM² + AC² - 2AC.CN + CN²

= AB(AB - 2BM) + AC(AC - 2CN) + BM² + CN²

= AB(2BE - 2BM) + AC(2CF - 2CN) + BM² + CN²

= 2AB(BE - BM) - 2AC(CN - CF) + BM² + CN²

= 2AB.EM - 2AC.FN + BM² + CN² (3)

+) Lại có:

DDEM ᔕ DDFN (g.g)

$\Rightarrow \frac{E M}{F N} = \frac{D E}{D F} = \frac{\frac{A C}{2}}{\frac{A B}{2}} = \frac{A C}{A B}$

Û AB.EM = AC.FN (4)

Thay (4) vào (3) suy ra (3) trở thành

MN² = BM² + CN² (đpcm).

Câu 5

Cho x, y là hai số thực thỏa mãn điều kiện x² + 2y² + 2xy + 7x + 7y + 10 = 0. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức $P = \frac{2 x + 2 y - 3}{x + y + 6} .$

Xem đáp án

Lời giải

Ta có:

x² + 2y² + 2xy + 7x + 7y + 10 = 0

Û (x² + 2xy + y²) + 7x + 7y + y² + 10 = 0

Û (x + y)² + 7(x + y) + y² + 10 = 0 (1)

Đặt S = x + y nên suy ra phương trình (1) trở thành

(1) Û S² + 7S + y² + 10 = 0

$\Leftrightarrow S^{2} + 7 S + \frac{49}{4} = \frac{9}{4} - y^{2}$

$\Leftrightarrow {(S + \frac{7}{2})}^{2} = \frac{9}{4} - y^{2} \leq \frac{9}{4}$

Dấu “=” xảy ra Û $\frac{9}{4} - y^{2} = \frac{9}{4} \Leftrightarrow y = 0$

Vậy ${(S + \frac{7}{2})}^{2} \leq \frac{9}{4}$

\Leftrightarrow \frac{- 3}{2} \leq S + \frac{7}{2} \leq \frac{3}{2}

Û - 5 £ S £ -2

$P = \frac{2 x + 2 y - 3}{x + y + 6} = \frac{2 (x + y + 6) - 15}{x + y + 6}$

$= 2 - \frac{15}{x + y + 6} = 2 - \frac{15}{S + 6}$ (2)

Với - 5 £ S £ -2

Û 1 £ S + 6 £ 4

$\Leftrightarrow \frac{15}{4} \leq \frac{15}{S + 6} \leq 15$

$\Leftrightarrow 2 - 15 \leq 2 - \frac{15}{S + 6} \leq 2 - \frac{15}{4}$

$\Leftrightarrow - 13 \leq 2 - \frac{15}{S + 6} \leq - \frac{7}{4}$

$\Leftrightarrow - 13 \leq P \leq - \frac{7}{4}$

Vậy suy ra GTNN của P = -13 $\Leftrightarrow \{\begin{matrix} x = - 5 \\ y = 0 \end{matrix}$

Và GTLN của $P = \frac{- 7}{4} \Leftrightarrow \{\begin{matrix} x = - 2 \\ y = 0 \end{matrix} .$

Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 9

🔥 Đề thi HOT:

15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án

15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án

10 Bài tập Nhận biết đơn thức, đơn thức thu gọn, hệ số, phần biến và bậc của đơn thức (có lời giải)

Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)

15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án

10 Bài tập Tìm giá trị đơn thức khi biết giá trị của biến (có lời giải)

10 Bài tập Thu gọn đơn thức (có lời giải)

15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 3: Phép cộng và phép trừ đa thức có đáp án

Nội dung liên quan:

Top 11 Đề kiểm tra Đại số Toán 8 Học Kì 1 Chương 1 có đáp án, cực hay

Top 8 Đề kiểm tra Đại Số Toán 8 Học Kì 1 Chương 2 có đáp án, cực hay

Top 8 Đề kiểm tra Toán 8 Học Kì 1 Chương 1 Hình học có đáp án, cực hay

Top 6 Đề kiểm tra Toán 8 Học Kì 1 Chương 2 Hình học có đáp án, cực hay

Top 4 Đề thi Toán 8 Học kì 1 có đáp án, cực sát đề chính thức

Đề thi Toán 8 Học kì 1 có đáp án, cực hay

Đề thi Toán lớp 8 Học kì 1 năm 2020 - 2021 cực hay, có đáp án

Đề thi Giữa kì 1 Toán 8 có đáp án

Đề kiểm tra Giữa kì 1 Toán 8 có đáp án (Mới nhất)

Bộ đề kiểm tra Học kì 1 Toán 8 có đáp án (Mới nhất)

Danh sách câu hỏi:

Cho biểu thức P=x−1x2−2x+x+1x2+2x−4x3−4x:1−2x. a) Tìm điều kiện xác định và rút gọn biểu thức P. b) Tính giá trị của biểu thức P biết x là số thực thỏa mãn điều kiện: |2x - 1| = 5.

Giải các phương trình và bất phương trình sau: a) 2x+12x2+5x+2−3x2−4=2; b) |x - 3| - |x2 - x + 1| = 1; c) (x2 - 1)(x3 + 1) ³ 0.

Cho x, y là hai số thực thỏa mãn điều kiện x2 + 2y2 + 2xy + 7x + 7y + 10 = 0. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức P=2x+2y−3x+y+6.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Giải các phương trình và bất phương trình sau:

a) $\frac{2 x + 1}{2 x^{2} + 5 x + 2} - \frac{3}{x^{2} - 4} = 2;$

b) |x - 3| - |x² - x + 1| = 1;

c) (x² - 1)(x³ + 1) ³ 0.

Cho x, y là hai số thực thỏa mãn điều kiện x² + 2y² + 2xy + 7x + 7y + 10 = 0. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức $P = \frac{2 x + 2 y - 3}{x + y + 6} .$