Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 7
25 người thi tuần này 4.0 21.8 K lượt thi 6 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 10
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 09
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 08
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 07
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 06
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 05
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 04
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 03
Danh sách câu hỏi:
Lời giải
1) Ta có: 2(2x − 1) − x = 4
4x – 2 – x = 4
4x – x = 4 +2
3x = 6
x = 2
Vậy tập nghiệm của phương trình là S = {2}.
2) Ta có: + =
ĐKXĐ: x ≠ 2 và x ≠ 0
+ =
+ =
x.(x + 1) + x – 2 = 5x – 4
x2 + x + x – 2 = 5x – 4
x2 + x + x – 5x – 2 + 4 = 0
x2 – 3x + 2 = 0
x2 – x – 2x + 2 = 0
x(x – 1) – 2(x – 1) = 0
(x – 1). (x – 2) = 0
Ta thấy chỉ có x = 1 thỏa mãn điều kiện.
Vậy tập nghiệm của phương trình là S = {1}.
Lời giải
1) Ta có: 3(x + 2) > 2x – 1
3x + 6 > 2x – 1
3x – 2x > – 1 – 6
x > – 7.
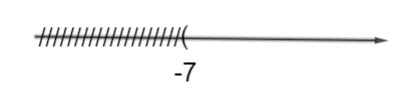
Vậy bất phương trình có tập nghiệm là S = (–7; +∞).
Biểu diễn tập nghiệm của bất phương trình trên trục số là:
2) Ta có: − ≥ + 3 (1)
Nhân cả hai vế của bất phương trình (1) với 12 ta được:
− ≥ + 3.12
− ≥ + 3.12
6. (x + 1) – 4. (3x – 5) ≥ 3x + 36
6x + 6 – 12x + 20 ≥ 3x + 36
6x – 12x – 3x ≥ 36 – 6 – 20
– 9x ≥ 10
x ≤ .
Vậy tập nghiệm của bất phương trình là:
Biểu diễn tập nghiệm của bất phương trình là:
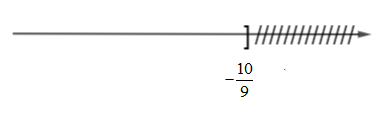
Lời giải
Gọi x (áo) là số áo mà xưởng phải dệt theo kế hoạch (x ∈ ℕ*)
Theo kế hoạch xưởng sẽ dệt xong số áo trong (ngày)
Thực tế, số áo may được là x + 20 (cái)
Số ngày thực tế là: (ngày)
Vì xưởng đã hoàn thành trước thời hạn 3 ngày nên:
= + 3
– =
40x – 30x = 4200
x = 420 (cái áo)
Vậy số áo xưởng phải dệt theo kế hoạch phân là 420 cái áo.
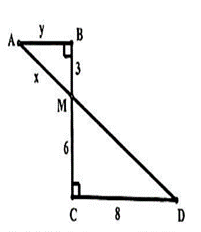
Lời giải
Áp dụng định lý Pytago vào ∆ DCM vuông tại C ta được:
DM2 = CM2 + CD2 = 62 + 82 = 100
DM = 10
Xét ∆ ABM và ∆ DCM ta có:
= (2 góc đối đỉnh)
= = 90°
Do đó ∆ABM ᔕ ∆DCM (g.g)
= =
= =
y = = 4
x = = 5
Vậy x = 5 và y = 4.
Lời giải
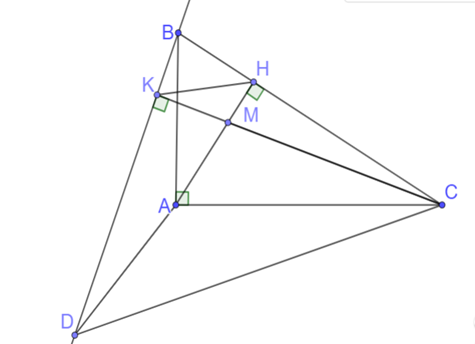
a) Vì ∆ ABC vuông tại A nên = 90°
Vì AH ⊥ BC nên = 90°
Xét ∆ ABC và ∆ HBA ta có:
Chung
= = 90°
Do đó ∆ ABC ᔕ ∆ HBA (g.g)
b) Vì AH ⊥ BC nên = 90°
Vì AM ⊥ BD tại K nên = 90°
Xét ∆CHM và ∆CBK ta có:
Chung
= = 90°
Do đó ∆ CHM ᔕ ∆ CBK (g.g)
=
CH. CK = CM. CB (đpcm)
c) Xét ∆CMH và ∆DMK, có:
(2 góc đối đỉnh)
⇒ ∆CMH ᔕ ∆DMK (g – g)
⇒ (hai cạnh tương ứng)
⇒
Xét ∆MHK và ∆MCD, có:
(cmt)
(2 góc đối đỉnh)
⇒ ∆MHK ᔕ ∆MCD (c – g – c)
⇒ (2 góc tương ứng)
Ta lại có:
(∆CDH vuông tại H)
(hai góc phụ nhau)
Mà (cmt)
hay = .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.