Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 5

a) ĐKXĐ: $\{\begin{array}{l}x\ne 0\\ x-2\ne 0\\ x+2\ne 0\end{array}\iff \{\begin{array}{l}x\ne 0\\ x\ne \pm 2\end{array}$

Ta có: $A=(\frac{1}{x-2}+\frac{2x}{x^2-4}+\frac{1}{x+2})(\frac{2}{x}-1)$

$=[\frac{1}{x-2}+\frac{2x}{(x-2)(x+2)}+\frac{1}{x+2}].\frac{2-x}{x}$

$=[\frac{x+2}{(x-2)(x+2)}+\frac{2x}{(x-2)(x+2)}+\frac{x-2}{(x-2)(x+2)}].\frac{-(x-2)}{x}$

$=\frac{x+2+2x+x-2}{(x-2)(x+2)}.\frac{-(x-2)}{x}$

$=\frac{4x}{x+2}.\frac{-1}{x}=\frac{-4}{x+2}$.

Vậy $A=(\frac{1}{x-2}+\frac{2x}{x^2-4}+\frac{1}{x+2})(\frac{2}{x}-1)=\frac{-4}{x+2}$.

 b) Ta có A = 1 hay $\frac{-4}{x+2}=1$.

Û x + 2 = − 4

Û x = − 6 (TMĐK).

Vậy để A =1 thì x = − 6.

a) |x – 9| = 2x + 5

• Với x ≥ 9 thì |x – 9| = x – 9.

Khi đó: x – 9 = 2x + 5

Û 2x – x = – 9 – 5

Û x = − 14 (loại).

• Với x < 9 thì |x – 9| = 9 – x.

Khi đó:  9 – x = 2x + 5

Û 2x + x = 9 – 5

Û 3x = 4

$\iff x=\frac{4}{3}$ (TMĐK).

Vậy tập nghiệm của phương trình đã cho là $S=\left\{\frac{4}{3}\right\}$.

b) $\frac{1-2x}{4}-2\le \frac{1-5x}{8}+x$

$\iff \frac{2(1-2x)}{8}-\frac{16}{8}\le \frac{1-5x}{8}+\frac{8x}{8}$

Û 2(1 – 2x) – 16 ≤ 1 – 5x + 8x

Û 2 – 4x – 16 ≤ 1 + 3x

Û – 4x – 3x ≤ 1 – 2 + 16

Û – 7x ≤ 15

$\iff x\ge \frac{-15}{7}$.

Vậy tập nghiệm của bất phương trình là $S=\left\{x|x\ge \frac{-15}{7}\right\}$.

Gọi x (km/h) vận tốc của tàu khi nước yên lặng (x > 4).

Đổi: 8 giờ 20 phút = $\frac{25}{3}$ giờ.

Vận tốc của tàu khi xuôi dòng là: x + 4 (km/h).

Vận tốc của tàu khi ngược dòng là: x − 4 (km/h).

Thời gian tàu đi xuôi dòng là: $\frac{80}{x+4}$ (giờ).

Thời gian tàu đi ngược dòng là: $\frac{80}{x-4}$ (giờ).

Vì thời gian cả đi lẫn về là 8 giờ 20 phút hay $\frac{25}{3}$ giờ nên ta có phương trình:

$\frac{80}{x+4}+\frac{80}{x-4}=\frac{25}{3}$

$\iff \frac{16}{x+4}+\frac{16}{x-4}=\frac{5}{3}$

$\iff \frac{48(x-4)}{3(x+4)(x-4)}+\frac{48(x+4)}{3(x+4)(x-4)}=\frac{5(x+4)(x-4)}{3(x+4)(x-4)}$

$\Rightarrow$ 48(x – 4) + 48(x + 4) = 5(x + 4)(x – 4)

Û 48(x – 4 + x + 4) = 5(x² – 16)

Û 96x = 5x² – 80

Û 5x² – 96x – 80 = 0

Û (x – 20)(5x + 4) = 0

Û x = 20 (TM) hoặc $x=\frac{-4}{5}$ (loại)

Vậy vận tốc của tàu khi nước yên lặng là 20 km/h.

Ta có ABCD là hình bình hành nên:

+ AD // BC hay BF // AD.

Khi đó: $\widehat{EDA}=\widehat{EBF}$; $\widehat{EAD}=\widehat{EFB}$ (các cặp góc so le trong).

+ AB // CD hay AB//GD.

$\widehat{DGE}=\widehat{BAE}$ (hai góc so le trong).

Xét ∆DEA và ∆BEF có:

$\widehat{EDA}=\widehat{EBF}$ (cmt).

$\widehat{EAD}=\widehat{EFB}$ (cmt).

Do đó ∆DEA  ∆BEF (g.g).

Xét ∆DGE và ∆BAE có:

$\widehat{DGE}=\widehat{BAE}$ (cmt)

$\widehat{DEG}=\widehat{BEA}$ (hai góc đối đỉnh)

Do đó ∆DGE ∆BAE (g.g).

Vậy ∆DEA ∆BEF và ∆DGE  ∆BAE.

b) Theo câu a, ta có:

+ ∆DEA ∆BEF suy ra: $\frac{EA}{EF}=\frac{DE}{BE}$ (1)

+ ∆DGE ∆BAE suy ra:  ^{$\frac{DE}{BE}=\frac{EG}{EA}$} (2)

Từ (1) và (2) suy ra $\frac{EA}{EF}=\frac{EG}{EA}$.

Do đó: EA² = EF . FG (đpcm).

c) Theo câu a, ta có:

+ ∆DEA ∆BEF suy ra: $\frac{DA}{BF}=\frac{DE}{BE}$ (3)

+ ∆DGE ∆BAE suy ra: $\frac{DE}{BE}=\frac{DG}{BA}$ (4)

Từ (3) và (4) suy ra $\frac{DA}{BF}=\frac{DG}{BA}$.

Do đó: BF . DG = AD . AB (không đổi).

Vậy BF . DG không đổi khi F thay đổi trên BC.

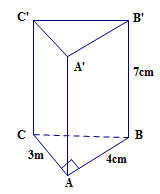
Áp dụng định lí Py-ta-go vào ∆ABC vuông tại A, ta có:

BC² = AB² + AC² = 3² + 4² = 25.

Suy ra: BC = 5 cm.

Ta có: S_xq = (AB +AC + BC) . BB’

= (3 + 4 + 5) . 7 = 84 (cm²).

Vậy diện tích xung quanh của hình lăng trụ là 84 cm².