Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 6)

a) 2x² – 5x + 2 = 0

Cách 1:

Ta có D = (–5)² – 4.2.2 = 9 > 0

Khi đó phương trình đã cho có hai nghiệm phân biệt

$x_1=\frac{5+\sqrt{9}}{2.2}=2$ và $x_2=\frac{5-\sqrt{9}}{2.2}=\frac{1}{2}$

Vậy phương trình đã cho có tập nghiệp $S=\left\{2;\frac{1}{2}\right\}$

Cách 2:

2x² – 5x + 2 = 0

Û x² − $\frac{5}{2}$ x + 1 = 0

Û x² − $\frac{1}{2}$ x – 2x + 1 = 0

Û x$\left(x-\frac{1}{2}\right)$  − 2$\left(x-\frac{1}{2}\right)$  = 0

Û (x – 2)$\left(x-\frac{1}{2}\right)$ = 0

Û$\left[\begin{array}{c}x-2=0\\ x-\frac{1}{2}=0\end{array}\right.$  Û $\left[\begin{array}{c}x=2\\ x=\frac{1}{2}\end{array}\right.$ .

Vậy phương trình đã cho có tập nghiệp $S=\left\{2;\frac{1}{2}\right\}$

b) x⁴ + x² – 6 = 0   (1)

Đặt t = x² (t ≥ 0), phương trình (1) trở thành:

t² + t – 6 = 0           (2)

Ta có hai cách giải phương trình (2) như sau:

Cách 1:

Ta có D = 1² – 4.1.(–6) = 25 > 0

Khi đó phương trình đã cho có hai nghiệm phân biệt là:

$t_1=\frac{-1+\sqrt{25}}{2.1}=2$ (thỏa mãn) và  $t_2=\frac{-1-\sqrt{25}}{2.1}=-3$ (không thỏa mãn)

Cách 2:

t² + t – 6 = 0           (2)

Û t² – 2t + 3t – 6 = 0

Û t(t – 2) + 3(t – 2) = 0

Û (t – 2)(t + 3) = 0

Û $\left[\begin{array}{c}t-2=0\\ t+3=0\end{array}\right.$

Û t = 2 (thỏa mãn) hay t = −3 (không thỏa mãn).

Với t = 2, ta có: x² = 2

Û x = $\sqrt{2}$  hoặc x = $-\sqrt{2}$ .

Vậy phương trình đã cho có tập nghiệm $S=\left\{\sqrt{2};-\sqrt{2}\right\}.$

+ Vẽ (P): y =  $\frac{x^2}{2}$

Bảng giá trị

Do đó (P) là đồ thị đi qua các điểm:

A(−2; 2); $B\left(-1;\frac{1}{2}\right)$ ; O(0; 0);$C\left(1;\frac{1}{2}\right)$ ; D(2; 2).

+ Vẽ (D): y = −3x – 4

Đường thẳng (D): y = −3x – 4 có a = −3, b = −4 đi qua 2 điểm M(0; b) và N$\left(\frac{-b}{a};0\right)$

Do đó 2 điểm thuộc đường thẳng (D) là M(0;−4) và N$\left(\frac{-4}{3};0\right)$ 

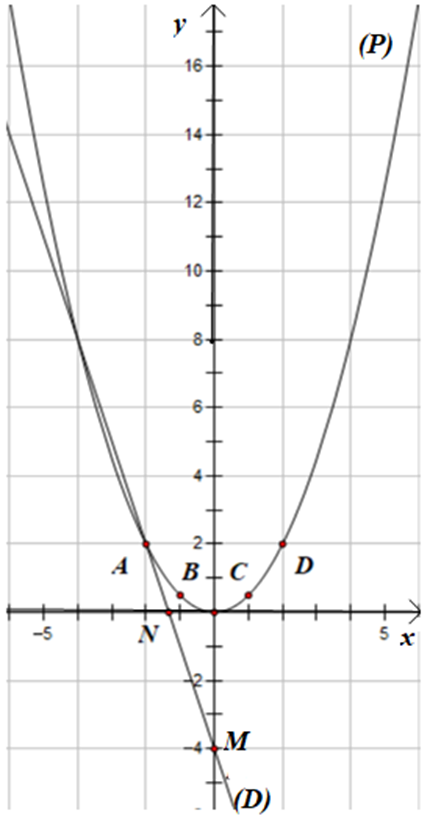
b) Phương trình hoành độ giao điểm của (P) và (D) là:

$\frac{1}{2}$x² = −3x – 4

Û x² = –6x – 8

Û x² + 6x + 8 = 0

Û x² + 4x + 2x + 8 = 0

Û x(x + 4) + 2(x + 4) = 0

Û (x + 4)(x + 2) = 0

Û $\left[\begin{array}{c}x+4=0\\ x+2=0\end{array}\right.$

Û $\left[\begin{array}{c}x=-2\\ x=-4\end{array}\right.$

• Thay x = −2 vào phương trình của (D): y = −3x – 4 ta được:

y = −3.(−2) − 4 = 2

Ta có tọa độ giao điểm là (−2; 2).

• Thay x = −4 vào phương trình của (D): y = −3x – 4 ta được:

y = −3.(−4) − 4 = 8

Ta có tọa độ giao điểm là (−4; 8).

Vậy tọa độ các giao điểm của (P) và (D) là (−2; 2) và (−4; 8).

x² + 2mx + m² + 2m – 2 = 0 có a = 1, b = 2m, c = m² + 2m – 2

Ta có:

∆ = b² – 4ac

= (2m)² – 4.1.(m² + 2m – 2)

= -8m + 8

a) Để phương trình (1) có hai nghiệm Û ∆ ≥ 0

Û −8m + 8 ≥ 0 Û m ≤ 1.

Vậy với m ≤ 1 thì phương trình (1) có hai nghiệm.

b) Với m ≤ 1, phương trình (1) có hai nghiệm x₁, x₂

Theo hệ thức Vi – ét ta có:

$\left\{\begin{array}{c}{x}_1+x_2=\frac{-b}{a}=-2m\\ x_1{x}_2=\frac{c}{a}=m^2+2m-2\end{array}\right.$

Ta có: x₁x₂ + x₁ + x₂ = 0

Û m² + 2m – 2 – 2m = 0

Û m² = 2

Û m = $\sqrt{2}$  (không thỏa mãn) hoặc m = $-\sqrt{2}$  (thỏa mãn)

Vậy m = $-\sqrt{2}$  thỏa mãn yêu cầu bài toán.

Gọi số học sinh tặng 3 quyển sách của lớp 9A là x (x ∈ ℕ*) (bạn).

Số học sinh tặng 5 quyển sách của lớp 9A là y (y ∈ ℕ*)  (bạn).

Vì lớp 9A có 42 học sinh nên ta có phương trình: x + y = 42 (1)

Vì cả lớp 9A đã tặng được 146 quyển sách nên ta có phương trình:

3x + 5y = 146 (2)

Từ (1) và (2), ta có hệ phương trình:

Û$\left\{\begin{array}{c}x+y=42\\ 3x+5y=146\end{array}\right.$

$\left\{\begin{array}{c}3x+3y=126\left(3\right)\\ 3x+5y=146\left(4\right)\end{array}\right.$

Ta lấy phương trình (4) trừ phương trình (3) vế theo vế ta được phương trình:

2y = 20

Û y = 10 (thỏa mãn)

Thay y = 10 vào phương trình (1) ta được:

x + 10 = 42 Û x = 32 (thỏa mãn)

Vậy lớp 9A có 32 bạn tặng 3 quyển sách và 10 bạn tặng 5 quyển sách.

a) Gọi y là số tiền mua kem (nghìn đồng) (y > 0).

x là số hộp kem mua được (hộp) (x > 3, x ∈ ℕ*).

Số tiền khi mua 3 hộp kem là:

3.40 = 120 (nghìn đồng)

Số hộp kem được tính với giá 20% là:

x – 3 (hộp kem)

Giá mỗi hộp kem (từ hộp thứ tư trở đi) là:

(100% – 20%).40 = 32 (nghìn đồng)

Số tiền cần trả khi mua nhiều hơn 3 hộp kem là:

y = 120 + (x – 3).32

= 32x + 24 (nghìn đồng).

b) Gọi a (hộp) là số hộp kem Bình mua (a > 3, a ∈ ℕ*)

Khi đó số hộp kem An mua là 2a (hộp kem)

Vì tổng số tiền mua kem của hai bạn là 624 nghìn đồng nên ta có phương trình:

32a + 24 + 32.2a + 24 = 624

Û 96a = 576 Û a = 6 (thỏa mãn).

Vậy Bình mua 6 hộp kem.