Đề kiểm tra giữa học kì 2 môn Toán 9 ( Mới nhất)_ đề 12
28 người thi tuần này 4.6 20 K lượt thi 5 câu hỏi 90 phút
- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
12 bài tập Một số bài toán thực tế liên quan đến độ dài cung tròn, diện tích hình quạt tròn và hình vành khuyên có lời giải
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
15 câu trắc nghiệm Toán 9 Kết nối tri thức Bài 13. Mở đầu về đường tròn có đáp án
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
1) Khi x = 25 (TMĐK) ta có:
.
Vậy giá trị của A khi x = 25 là .
2)
.
3) P = A.B
=
Ta có
.
Vậy giá trị lớn nhất của P là . Dấu bằng xảy ra khi .
Lời giải
Gọi x (sản phẩm) là số sản phẩm mà tổ I làm trong tháng đầu (0 < x < 600, x ∈ ℕ).
y (sản phẩm) là số sản phẩm mà tổ II làm trong tháng đầu (0 < y < 600, y ∈ ℕ).
Trong tháng đầu, hai tổ làm được 600 sản phẩm ta có:
x + y = 600 (sản phẩm) (1)
Số sản phẩm mà tổ I làm được trong tháng hai là:
x + 10%x = 1,1x (sản phẩm)
Số sản phẩm mà tổ II làm được trong tháng hai là:
y + 20%y = 1,2y (sản phẩm)
Tháng thứ hai cả hai tổ làm được 685 sản phẩm ta có:
1,1x + 1,2y = 685 (sản phẩm) (2)
Từ (1) và (2) ta có hệ phương trình:
(thỏa mãn)
Vậy trong tháng thứ nhất tổ I làm được 350 sản phẩm, tổ II làm được 250 sản phẩm.
Lời giải
1) Phương trình hoành độ giao điểm của (P) và (d) là:
x2 = x + 2
Û x2 – x – 2 = 0
Û x2 – 2x + x −2 = 0
Û x(x – 2) + (x – 2) = 0
Û (x + 1)(x − 2) = 0
• Với x = −1 thì y = x + 2 = –1 + 2 = 1.
Do đó, ta có tọa độ giao điểm của (P) và (d) là A(−1; 1).
• Với x = 2 thì y = x + 2 = 2 + 2 = 4.
Do đó, ta có tọa độ giao điểm của (P) và (d) là B(2; 4).
Vậy hai đồ thị hàm số trên có 2 giao điểm là A(−1; 1) và B(2; 4).
Vẽ (P)
Bảng giá trị:
|
x |
−2 |
−1 |
0 |
1 |
2 |
|
y = x2 |
4 |
1 |
0 |
1 |
4 |
Vẽ (d)
(d) y = x + 2 đi qua 2 điểm A(−1; 1) và B(2; 4).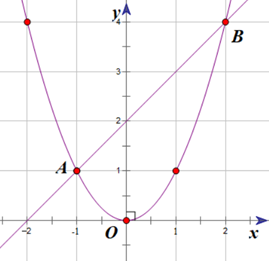
2) Để hệ phương trình có nghiệm duy nhất thì:
Giải hệ phương trình với m là tham số
Để hệ có nghiệm x, y nguyên thì
nguyên nguyên
Xét
Để nguyên thì m + 1 bằng các giá trị {−1; 1}.
Do đó m ∈ {−2; 0} (thỏa).
Vậy m ∈ {−2; 0} thì hệ phương trình có nghiệm duy nhất nguyên.
Lời giải
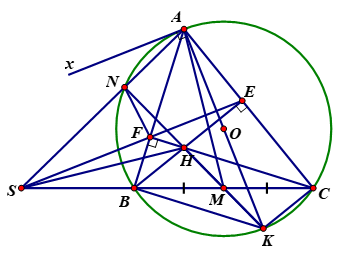
) Ta có (CF ⊥ AB)
(BE ⊥ AC)
Xét tứ giác BFEC có
Suy ra tứ giác BFEC nội tiếp.
2) Từ A kẻ tiếp tuyến Ax của (O)
Ta có (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cùng chắn cung AB)
Mà (tứ giác FECB nội tiếp)
Suy ra Ax // FE (hai góc so le trong)
Mà Ax ⊥ AO (Ax là tiếp tuyến của (O))
Suy ra FE ⊥ OA (điều phải chứng minh)
3) Ta có: (góc nội tiếp chắn nửa đường tròn)
(góc nội tiếp chắn nửa đường tròn)
Xét tứ giác BHCK có:
BH // CK (cúng vuông góc AC)
CH // BK (cùng vuông góc AB)
Suy ra tứ giác BHCK là hình bình hành
Tứ giác BHCK là hình bình hành có M là trung điểm BC
Suy ra M cũng là trung điểm HK suy ra M, H, K thẳng hàng
SA cắt đường tròn (O) tại N
Xét tứ giác nội tiếp BFEC có FE cắt BC tại S
Xét ∆SFB và ∆SCE có:
là góc chung
(tứ giác BFEC nội tiếp)
Suy ra ∆SFB ![]() ∆SCE (g.g)
∆SCE (g.g)
Suy ra
Tương tự tứ giác BNAC nội tiếp (O) có AN cắt CB tại S.
Suy ra SN.SA = SB.SC
Từ 2 điều trên suy ra SN.SA = SF.SE
Xét ∆SNF và ∆SEA có:
là góc chung
(chứng minh trên)
Do đó ∆SNF ![]() ∆SEA (c.g.c)
∆SEA (c.g.c)
Suy ra .
Suy ra tứ giác ANFE nội tiếp (1)
Ta có (CF ⊥ AB)
(BE ⊥ AC)
Xét tứ giác AFHE có
Suy ra tứ giác AFHE nội tiếp. (2)
Từ (1) và (2) suy ra A, N, F, H, E nội tiếp cùng một đường tròn.
Có (BE ⊥ AC) AH là đường kính .
Suy ra (góc nội tiếp chắn nửa đường tròn)
.
Ta có (góc nội tiếp chắn nửa đường tròn)
.
Mà NH ⊥ SA (cmt).
Suy ra K, H, N thẳng hàng hay 4 điểm K, M, H, N thẳng hàng.
Suy ra MH ⊥ SA.
Xét tam giác ABC có H là giao điểm của 2 đường cao CF và BE.
Suy ra AH là dường cao thứ ba suy ra AH ⊥ BC hay AH ⊥ SM.
Xét tam giác ASM có:
MH ^ SA (cmt);
AH ^ SM (cmt).
Suy ra H là trực tâm của tam giác ASM.
Vậy SH ⊥ AM (điều phải chứng minh).
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki, ta có:
Xét S2 =
![]()
Vậy Max S
Dấu bằng xảy khi .
Mà x2 + y2 + z2 = 6 nên x = y = z = .
Do 1 ≤ x ≤ 2 Û 1 ≤ x2 ≤ 4 Û 3 ≥ 4 – x2 ≥ 0 .
Tương tự ta có: , .
Áp dụng tính chất: 0 ≤ a ≤ 1 thì .
Ta có:
.
Vậy Min S = khi (a; b; c) là hoán vị (2; 1; 1).