50 bài tập Nguyên hàm, tích phân và ứng dụng có lời giải
181 người thi tuần này 4.6 4 K lượt thi 50 câu hỏi 50 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Cụm trường THPT Hà Tĩnh có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Sở Phú Thọ có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Đồng Hỷ (Thái Nguyên) có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Chuyên Trần Phú (Hải Phòng) lần 1 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Lê Quý Đôn (Hà Nội) lần 01 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Nguyễn Khuyến (TP.HCM) có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Cửa Lò (Nghệ An) có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Chuyên Hạ Long lần 01 có đáp án
Danh sách câu hỏi:
Câu 1
A. \(f\left( x \right) = 2x{e^{{x^2}}}\).
B. \(f\left( x \right) = {x^2}{e^{{x^2}}} - 1\).
C. \(f\left( x \right) = {e^{2x}}\).
D. \(f\left( x \right) = \frac{{{e^{{x^2}}}}}{{2x}}\).
Lời giải
Câu 2
A. \(F\left( x \right) = - \cos x - \sin x + C\).
B. \(F\left( x \right) = \cos x + \sin x + C\)
Lời giải
Ta có:
Chọn D.
Câu 3
Lời giải
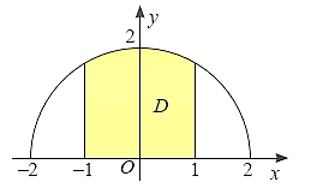
Xét \(x \in \left[ {0;2} \right]\), ta có \({2^x} \ge {2^0} \Leftrightarrow {2^x} \ge 1\) nên \(\left| {{2^x} - 1} \right| = {2^x} - 1\).
Diện tích hình phẳng cần tính là \(S = \int\limits_0^2 {\left| {{2^x} - 1} \right|{\rm{d}}x} = \int\limits_0^2 {\left| {1 - {2^x}} \right|{\rm{d}}x} = \int\limits_0^2 {\left( {{2^x} - 1} \right){\rm{d}}x} \). Chọn C.
Câu 4
Lời giải
Ta có . Chọn B.
Câu 5
Lời giải
Vận tốc của ô tô là \(v\left( t \right) = \int {a\left( t \right){\rm{dt}}} \)\( = \int {\left( { - \frac{8}{5}t} \right){\rm{dt}}} \)\( = - \frac{4}{5}{t^2} + C\).
Ta có \(72\,{\rm{km/h}} = 20\,{\rm{m/s}}\). Vì \(v\left( 0 \right) = 20\) nên \(C = 20\)\( \Rightarrow v\left( t \right) = - \frac{4}{5}{t^2} + 20\).
Khi xe dừng hẳn thì vận tốc bằng \(0\) nên \( - \frac{4}{5}{t^2} + 20 = 0 \Rightarrow t = 5\).
Quãng đường cần tìm là \(s = \int\limits_0^5 {\left( { - \frac{4}{5}{t^2} + 20} \right)} \,{\rm{dt}}\)\( = \left. {\left( { - \frac{4}{{15}}{t^3} + 20t} \right)} \right|_0^5\)\( = \frac{{200}}{3}\,\,\,\left( {\rm{m}} \right)\). Chọn C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A. \(2{F_1}\left( x \right) - {F_2}\left( x \right) + C\).
B. \({F_2}\left( x \right) - {F_1}\left( x \right) + C\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
A. \(\int {f\left( x \right){\rm{d}}x = } \frac{{{x^3}}}{3} - \frac{1}{x} + C\).
B. \(\int {f\left( x \right){\rm{d}}x = } \frac{{{x^3}}}{3} + \frac{2}{x} + C\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
A. \(F\left( x \right) = {x^2} + {e^x} + 2023\).
B. \(F\left( x \right) = {x^2} + {e^x} - 2023\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
A. \[{e^x} - \frac{1}{2}{e^{ - 2x}} + C\].
B. \[\frac{{{{25}^x}}}{{2\ln 5}} + 12{e^{ - \frac{x}{2}}} + C\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 26
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 27
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 28
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 31
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 32
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 33
A. \(S = \int\limits_a^c {f\left( x \right){\rm{d}}x + \int\limits_c^b {f\left( x \right){\rm{d}}x} } .\)
B. \[S = \int\limits_a^b {f\left( x \right){\rm{d}}x} .\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 34
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 35
D. \(V = \int\limits_0^2 {{e^{2x}}} \;{\rm{d}}x\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 36
A. \[f\left( c \right) > f\left( a \right) > f\left( b \right)\].
B. \[f\left( c \right) > f\left( b \right) > f\left( a \right)\].
C. \[f\left( a \right) > f\left( b \right) > f\left( c \right)\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 37
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 38
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 39
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 40
A. \[\frac{2}{3}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 41
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 42
A. \[\frac{{11\pi }}{3}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
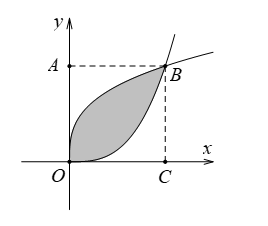
![Cho đồ thị hàm số \(y = {{\rm{e}}^x}\) và hình được tô màu như hình bên. a) Hình phẳng được tô màu giới hạn bởi \[3\] đường. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid0-1735917286.png)
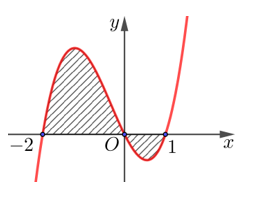
![Diện tích của hình phẳng được giới hạn bởi đồ thị hàm số \[y = f\left( x \right)\] như vẽ hình bên, trục hoành và hai (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid0-1736178868.png)
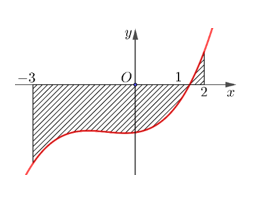
![Cho hàm số \[y = f\left( x \right)\] có đồ thị \[y = f'\left( x \right)\] cắt trục \[Ox\] tại ba điểm có hoành (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid2-1736179204.png)
![Cho một vật thể bằng gỗ có dạng hình trụ với chiều cao và bán kính đáy cùng bằng \[R\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid8-1736179875.png)