Lấy ngẫu nhiên một viên bi, rồi lấy ngẫu nhiên một viên bi nữa từ một bình đựng 5 bi xanh và 3 bi đỏ $\Rightarrow n_{Ω} = C_{8}^{1} . C_{7}^{1} = 56$ .

Biến cố A: “Lấy lần thứ hai được một viên bi xanh”.

Trường hợp 1: lần 1 lấy được bi đỏ và lần hai lấy được bi xanh: $C_{3}^{1} . C_{5}^{1} = 15$ cách.

Trường hợp 2: cả lần 1 và lần 2 đều lấy được bi xanh: $C_{5}^{1} . C_{4}^{1} = 20$ cách.

$\Rightarrow n (A) = 15 + 20 = 35$ .

$\Rightarrow P (A) = \frac{35}{56} = \frac{5}{8}$ .

Câu 2/50

Cho hàm số bậc ba y=f(x) có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên dương của m để phương trình f(x) = m có ba nghiệm phân biệt?

A. 3

B. 2

C. 4

D. 5

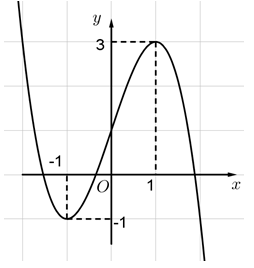
Lời giải

Đáp án đúng là: A

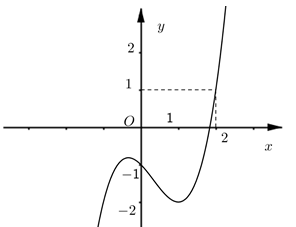
Phương trình $f (x) = m$ có 3 nghiệm phân biệt khi đường thẳng y = m cắt đồ thị hàm số $y = f (x)$ tại 3 điểm phân biệt.

$\Leftrightarrow - 1 < m < 3$ .

Mà $m \in ℤ \Rightarrow m \in \{0; 1; 2\}$

Vậy có 3 số nguyên thỏa mãn yêu cầu bài toán.

Câu 3/50

Hàm số $y = a x^{4} + b x^{2} + c$ với $a > 0$ có đồ thị là hình nào trong bốn hình dưới đây?

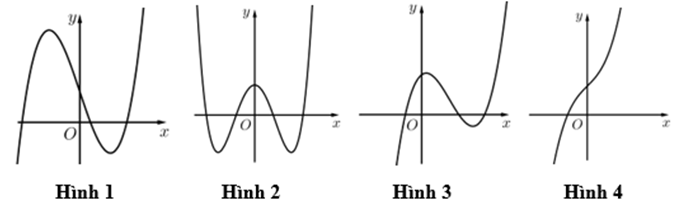
A. Hình 2

B. Hình 3

C. Hình 4

D. Hình 1

Lời giải

Đáp án đúng là: A

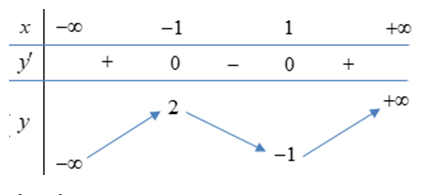
Đồ thị ở trong các hình 1, 3, 4 đều là đồ thị của các hàm số bậc 3 nên loại.

Chọn đáp án A là hình số 2.

Câu 4/50

Tập hợp điểm biểu diễn số phức z thỏa mãn điều kiện $|\bar{z} + 1 + 2 i| = 2$ là

A. Đường tròn I(-1;2), bán kính R = 2.

B. Đường tròn I(1;-2), bán kính R = 2.

C. Đường tròn I(-1;-2), bán kính R = 2.

D. Đường tròn I(1;2), bán kính R = 2.

Lời giải

Đáp án đúng là: A

Đặt $z = x + y i \Rightarrow \bar{z} = x - y i$ .

$|\bar{z} + 1 + 2 i| = 2 \Leftrightarrow {(x + 1)}^{2} + {(2 - y)}^{2} = 4$

Vậy tập hợp các điểm biểu diễn số phức z là đường tròn tâm $I (- 1; 2)$ và bán kính R = 2.

Câu 5/50

Khối lập phương có độ dài đường chéo là $5 \sqrt{3}$ . Thể tích của khối lập phương đã cho bằng

A. $\frac{125}{3}$

B. 125

C. 27

D. $25 \sqrt{3}$

Lời giải

Đáp án đúng là: B

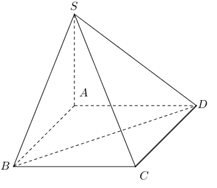
Đặt cạnh hình lập phương là x.

Khi đó đường chéo hình lập phương là $x \sqrt{3}$ .

$\Rightarrow x \sqrt{3} = 5 \sqrt{3} \Leftrightarrow x = 5$ .

Thể tích khối lập phương là $V = 5^{3} = 125$ .

Câu 6/50

Trong không gian Oxyz, góc giữa trục Oy và mp (Oxz) bằng

A. $120 °$

B. $60 °$

C. $90 °$

D. $45 °$

Lời giải

Đáp án đúng là: C

Ta có $\{\begin{cases} O y ⊥ O x \\ O y ⊥ O z \end{cases} \Rightarrow O y ⊥ (O x z)$ . Vậy góc giữa trục Oy và mp (Oxz) bằng $90 °$ .

Câu 7/50

Tiệm cận ngang của đồ thị hàm số $y = \frac{6}{x - 5}$ là

A. y = 6

B. x = 5

C. y = 0

D. y = - 6

Lời giải

Đáp án đúng là: C

$\lim_{x \to \pm \infty} y = \lim_{x \to \pm \infty} \frac{6}{x - 5} = 0 \Rightarrow y = 0$ là tiệm cận ngang của đồ thị hàm số đã cho.

Câu 8/50

Nếu $\int_{1}^{2} f (x) d x = 5$ và $\int_{1}^{3} f (x) d x = 15$ thì $\int_{2}^{3} f (x) d x$ bằng

A. 20

B. 25

C. 10

D. 3

Lời giải

Đáp án đúng là: C

$\int_{1}^{3} f (x) d x = \int_{1}^{2} f (x) d x + \int_{2}^{3} f (x) d x \Rightarrow \int_{2}^{3} f (x) d x = \int_{1}^{3} f (x) d x - \int_{1}^{2} f (x) d x = 15 - 5 = 10$

Câu 9/50

Cho hàm số $y = a x^{4} + b x^{2} + c$ có đồ thị như hình vẽ. Điểm cực đại của đồ thị hàm số đã cho có tọa độ là

A. (-1;-4)

B. (1;-4)

C. (-3;0)

D. (0;-3)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10/50

Trên khoảng $(0; + \infty)$ , đạo hàm của hàm số $y = x^{e}$ là

x^{e - 1}

\frac{x^{e + 1}}{e + 1}

e x^{e - 1}

(e - 1) x^{e - 1}

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11/50

Trong không gian Oxyz cho mặt cầu (S) có tâm $I (0; 0; - 3)$ và đi qua điểm $M (4; 0; 0) .$ Phương trình của (S) là

A. $x^{2} + y^{2} + {(z + 3)}^{2} = 5$

B. $x^{2} + y^{2} + {(z - 3)}^{2} = 25$

C. $x^{2} + y^{2} + {(z + 3)}^{2} = 25$

D. $x^{2} + y^{2} + {(z - 3)}^{2} = 5$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 12/50

Tập nghiệm của bất phương trình $e^{x^{2} - x + 1} < e$ là

A. $(1; + \infty)$

B. (1;2)

C. $(- \infty; 0)$

D. (0;1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 13/50

Cho hàm số y=f(x) có bảng biến thiên như sau:

Giá trị cực đại của hàm số đã cho là

A. 5

B. 2

C. 1

D. 0

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 14/50

Số cách sắp xếp 3 học sinh nam và 3 học sinh nữ vào một dãy ghế hàng ngang có 6 chỗ ngồi là

A. 6

B. 12

C. 26

D. 720

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 15/50

Cho $A (2; 1; - 1)$ và $(P) : x + 2 y - 2 z + 3 = 0$ . Goi d là đường thẳng đi qua A và vuông góc với (P). Tìm tọa độ M thuộc d sao cho $O M = \sqrt{3}$ .

A. $(1; - 1; 1); (\frac{5}{3}; \frac{1}{3}; - \frac{1}{3})$

B. $(1; - 1; - 1); (\frac{5}{3}; - \frac{1}{3}; \frac{1}{3})$

C. $(1; - 1; - 1); (\frac{5}{3}; \frac{1}{3}; \frac{1}{3})$

D. $(1; - 1; - 1); (\frac{5}{3}; \frac{1}{3}; - \frac{1}{3})$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 16/50

Cho số phức z = 2 -3i. Số phức $w = \frac{z - 2}{\bar{z} + 2 i}$ có phần thực bằng

A. $\frac{15}{29} .$

B. -15

C. 15

D. $\frac{- 15}{29} .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 17/50

Cho a là số thực dương khác 1. Giá trị của $\log_{\frac{1}{a}} a^{2023}$ là

A. 2023

B. $- \frac{1}{2023} .$

C. $\frac{1}{2023} .$

D. -2023

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 18/50

Cho hình chóp sabcd có đáy là hình vuông cạnh a, SA vuông góc với đáy và $S A = \frac{a \sqrt{6}}{2}$ (tham khảo hình vẽ). Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng

A. $45 ° .$

B. $60 ° .$

C. $30 ° .$

D. $90 ° .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 19/50

Cho hàm số $y = a x^{3} + b x^{2} + c x + d$ có đồ thị là đường cong trong hình bên. Toạ độ giao điểm của đồ thị đã cho và đường thẳng y = 1 là

A. (2;1)

B. (1;2)

C. (2;0)

D. (0;2)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 20/50

Cho khối chóp SABC có SA,AB,AC đôi một vuông góc. Biết SA= 3a, AB = 4a, AC = 2a. Thể tích V của khối chóp đã cho bằng

A. $V = 24 a^{3} .$

B. $V = 4 a^{3} .$

C. $V = 6 a^{3} .$

D. $V = 2 a^{3} .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem tiếp với tài khoản VIP

Còn 42/50 câu hỏi, đáp án và lời giải chi tiết.

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán