Đề thi ôn tốt nghiệp THPT Toán có lời giải ( Đề 2)
44 người thi tuần này 4.6 4.5 K lượt thi 22 câu hỏi 50 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Nguyễn Thị Minh Khai (Hà Nội) lần 1 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Liên trường THPT (Nghệ An) có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Chuyên Đại học Vinh lần 1 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Cụm liên trường Nghệ An có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Sở Bắc Ninh có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Chuyên ĐH KHTN Hà Nội lần 1 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Sở Hưng Yên có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Nguyễn Gia Thiều (Hà Nội) có đáp án
Danh sách câu hỏi:
Câu 1
Lời giải
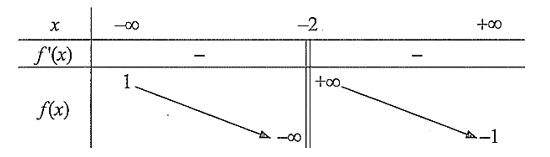
Dựa vào bảng biến thiên ta thấy:
Đồ thị hàm số có tiệm cận đứng là \(x = - 2\) và có 2 tiệm cận ngang là \(y = 1;y = - 1\).
Vậy tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là 3. Chọn C.
Câu 2
Lời giải
Ta có \(y' = {e^x}\left( {x - 1} \right)\). Bảng xét dấu của đạo hàm

Từ đó, hàm số nghịch biến trên khoảng \(\left( { - \infty ;1} \right)\). Chọn D.
Câu 3
Lời giải
Ta có \(f'\left( x \right) = 1 + \frac{4}{{{{\left( {x - 3} \right)}^2}}} > 0,\forall x \in \left[ { - 1;2} \right]\).
Suy ra \(M = \mathop {\max }\limits_{\left[ { - 1;2} \right]} f\left( x \right) = f\left( 2 \right) = 7;m = \mathop {\min }\limits_{\left[ { - 1;2} \right]} f\left( x \right) = f\left( { - 1} \right) = 1\). Vậy \(M - m = 6\). Chọn C.
Câu 4
Lời giải
Ta có \(y' = \frac{{ - 2m - 1}}{{{{\left( {x - m} \right)}^2}}},x \ne m\). Điều kiện \(\left\{ \begin{array}{l} - 2m - 1 > 0\\m \ge - 4\end{array} \right. \Leftrightarrow - 4 \le m < - \frac{1}{2}\).
Có bốn giá trị nguyên \(m\) thỏa mãn \( - 4; - 3; - 2; - 1\). Chọn B.
Câu 5
Lời giải
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
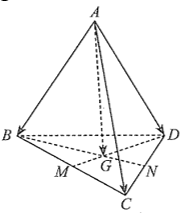
A. \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AG} \).
B. \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \).
C. \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AN} = 3\overrightarrow {AG} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.