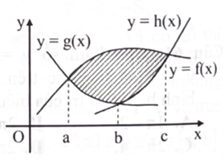
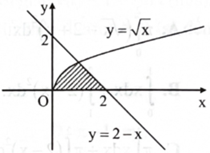
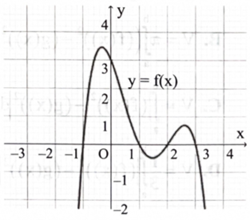
DẠNG 3. MỐI LIÊN HỆ GIỮA TÍCH PHÂN VÀ DIỆN TÍCH HÌNH PHẲNG
28 người thi tuần này 4.6 3.3 K lượt thi 24 câu hỏi 60 phút
🔥 Đề thi HOT:
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
33 K lượt thi
34 câu hỏi
CÂU TRẮC NGHIỆM ĐÚNG SAI
13 K lượt thi
20 câu hỏi
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
6.8 K lượt thi
34 câu hỏi
Đề số 01
13.5 K lượt thi
51 câu hỏi
Bộ Đề thi THPT Quốc gia chuẩn cấu trúc Bộ Giáo dục môn Toán 2019 (Đề số 1)
14.5 K lượt thi
50 câu hỏi
20 Bộ đề ôn luyện thi thpt quốc gia môn Toán có lời giải (Đề số 1)
7.7 K lượt thi
50 câu hỏi
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
158.3 K lượt thi
50 câu hỏi
Bộ đề thi thử Đại học môn Toán mới nhất cực hay có lời giải (Đề 1)
45.4 K lượt thi
50 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
A. \(S = \int_b^a f (x)dx.\)
B. \(S = \int_b^a | f(x)|dx.\)
C. \(S = \left| {\int_a^b f (x)dx} \right|.\)
D. \(S = \int_a^b | f(x)|dx.\)
Lời giải
Chọn đáp án D
Câu 2
A. \(S = \left| {\int_a^b {(f(} x) - g(x))dx} \right|.\)
B. \(S = \int_b^a \mid (f(x) - g(x))dx.\)
C. \(S = \int_a^b \mid (f(x) - g(x))dx.\)
D. \(S = \int_b^a {(f(} x) - g(x))dx.\)
Lời giải
Chọn đáp án C
Câu 3
A. \(\int_{\rm{a}}^{\rm{b}} {\rm{f}} ({\rm{x}}){\rm{dx}} = {\rm{S}}.\)
B. \(\int_a^b f (x)dx = (a - b)S.\)
C. \(\int_a^b f (x)dx = - S.\)
D. \(\int_a^b f (x)dx = (b - a)S.\)
Lời giải
Chọn đáp án A
Câu 4
A. \(\int_a^b f (x)dx = S.\)
B. \(\int_a^b f (x)dx = (a - b)S.\)
C. \(\int_a^b f (x)dx = - S.\)
D. \(\int_a^b f (x)dx = (b - a)S.\)
Lời giải
Chọn đáp án C
Câu 5
A. \({{\rm{S}}_1} + {{\rm{S}}_2}.\)
B. \({{\rm{S}}_1} - {{\rm{S}}_2}.\)
C. \( - {{\rm{S}}_1} + {{\rm{S}}_2}.\)
D. \( - {{\rm{S}}_1} - {{\rm{S}}_2}.\)
Lời giải
\(\int_a^b f (x)dx = \int_a^c f (x)dx + \int_c^b f (x)dx = {S_1} - {S_2}.\) Chọn B.
Câu 6
A. \({{\rm{S}}_1} + {{\rm{S}}_2}.\)
B. \({{\rm{S}}_1} - {{\rm{S}}_2}.\)
C. \( - {{\rm{S}}_1} + {{\rm{S}}_2}.\)
D. \( - {{\rm{S}}_1} - {{\rm{S}}_2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \({{\rm{S}}_1} + {{\rm{S}}_2}.\)
B. \({{\rm{S}}_1} - {{\rm{S}}_2}.\)
C. \( - {{\rm{S}}_1} + {{\rm{S}}_2}.\)
D. \( - {{\rm{S}}_1} - {{\rm{S}}_2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. \({{\rm{S}}_1} + {{\rm{S}}_2}.\)
B. \({{\rm{S}}_1} - {{\rm{S}}_2}.\)
C. \( - {{\rm{S}}_1} + {{\rm{S}}_2}.\)
D. \( - {{\rm{S}}_1} - {{\rm{S}}_2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. \({{\rm{S}}_1} + {{\rm{S}}_2}.\)
B. \({S_1} - {S_2}.\)
C. \( - {{\rm{S}}_1} + {{\rm{S}}_2}.\)
D. \( - {{\rm{S}}_1} - {{\rm{S}}_2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. \({{\rm{S}}_1} + {{\rm{S}}_2}.\)
B. \({{\rm{S}}_1} - {{\rm{S}}_2}.\)
C. \( - {{\rm{S}}_1} + {{\rm{S}}_2}.\)
D. \( - {{\rm{S}}_1} - {{\rm{S}}_2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. \({{\rm{S}}_1} + {{\rm{S}}_2}.\)
B. \({{\rm{S}}_1} - {{\rm{S}}_2}.\)
C. \( - {{\rm{S}}_1} + {{\rm{S}}_2}.\)
D. \( - {{\rm{S}}_1} - {{\rm{S}}_2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. \({{\rm{S}}_1} + {{\rm{S}}_2}.\)
B. \({{\rm{S}}_1} - {{\rm{S}}_2}.\)
C. \( - {{\rm{S}}_1} + {{\rm{S}}_2}.\)
D. \( - {{\rm{S}}_1} - {{\rm{S}}_2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A. \(4\pi - 2.\)
B. \(2\pi + 2.\)
C. \(2\pi - 4.\)
D. \(2\pi - 2.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A. \(\frac{4}{3}.\)
B. \(\frac{2}{3}.\)
C. \(\frac{8}{3}.\)
D. \(\frac{{20}}{3}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
A. \(\frac{{49}}{3}.\)
B. \(\frac{{29}}{3}.\)
C. \(\frac{{22}}{3}.\)
D. \(\frac{{32}}{3}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
A. \(\frac{1}{{\rm{e}}}.\)
B. \(1 - \frac{1}{{\rm{e}}}.\)
C. \({\rm{e}} - 1.\)
D. e.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
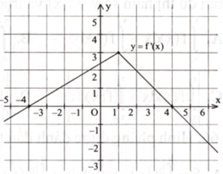
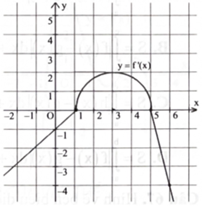
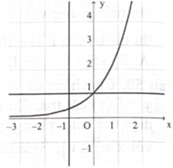
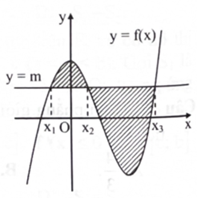
![Hình vẽ bên biểu diễn trục hoành cắt đồ thị hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) tại ba điểm có hoành độ \({{\rm{x}}_1},{{\rm{x}}_2},{{\rm{x}}_3}\) \(\left( {{x_1} < {x_2} < {x_3}} \right).\) Diện tích phần hình phẳng giới hạn bởi đồ thị hàm số \(y = f(x)\) và trục hoành là A. \(\int_{{x_1}}^{{x_2}} f (x)dx + \int_{{x_2}}^{{x_3}} f (x)dx.\) B. \(\int_{{x_1}}^{{x_2}} f (x)dx - \int_{{x_2}}^{{x_3}} f (x)dx.\) C. \[\left| {\int_{{x_1}}^{{x_2}} f (x)dx + \int_{{x_2}}^{{x_3}} f (x)dx} \right|.\] D. \(\left| {\int_{{{\rm{x}}_1}}^{{{\rm{x}}_3}} {\rm{f}} ({\rm{x}}){\rm{dx}}} \right|.\) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/09/blobid3-1727016691.png)
A. \(\int_{{x_1}}^{{x_2}} f (x)dx + \int_{{x_2}}^{{x_3}} f (x)dx.\)
B. \(\int_{{x_1}}^{{x_2}} f (x)dx - \int_{{x_2}}^{{x_3}} f (x)dx.\)
C. \[\left| {\int_{{x_1}}^{{x_2}} f (x)dx + \int_{{x_2}}^{{x_3}} f (x)dx} \right|.\]
D. \(\left| {\int_{{{\rm{x}}_1}}^{{{\rm{x}}_3}} {\rm{f}} ({\rm{x}}){\rm{dx}}} \right|.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A. \(S = \int_a^b | h(x) - g(x)|dx + \int_b^c | h(x) - f(x)|dx.\)
B. \(S = \int_a^c | f(x) - g(x)|dx + \int_b^c | f(x) - h(x)|dx.\)
C. \(S = \int_a^c | h(x) - g(x)|dx + \int_b^c | h(x) - f(x)|dx.\)
D. \(S = \int_a^b | f(x) - g(x)|dx + \int_b^c | f(x) - h(x)|dx.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
A. \(\int_{{x_1}}^{{x_2}} {(f(} x) - m)dx + \int_{{x_2}}^{{x_2}} {(f(} x) - m)dx.\)
B. \(\int_{{x_1}}^{{x_2}} {(f(} x) - m)dx - \int_{{x_2}}^{{x_2}} {(f(} x) - m)dx.\)
C. \(\int_{{x_1}}^{{x_2}} {(m - f(} x))dx + \int_{{x_2}}^{{x_2}} {(m - f(} x))dx.\)
D. \(\left| {\int_{{x_1}}^{{x_1}} {(f(} x) - m)dx} \right|.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
A. \(\int_0^2 {(\sqrt x - 2 + x)} dx.\)
B. \(\int_0^2 {(2 - x - \sqrt x )} dx.\)
C. \(\int_0^1 {\sqrt x } dx + \int_1^2 {(2 - x)} dx.\)
D. \(\int_0^2 {\sqrt x } dx + \int_0^2 {(2 - x)} dx.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
A. \(\int_1^2 {\left( {{2^x} - 2} \right)} dx.\)
B. \(\int_{ - 1}^2 {\left( {{2^x} - 2} \right)} dx.\)
C. \(\int_{ - 1}^2 {\left( {2 - {2^x}} \right)} dx.\)
D. \(\int_{ - 1}^1 {\left( {2 - {2^x}} \right)} dx + \int_1^2 {\left( {{2^x} - 2} \right)} dx.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo