19 câu Trắc nghiệm Phép đối xứng tâm có đáp án

Lấy hai điểm A, B bất kì lần lượt thuộc a, b. Trung điểm I của AB chính là tâm đối xứng của hình.

Vì A và B là 2 điểm bất kì nên có vô số điểm I thỏa mãn.

Chọn đáp án D

Phép đối xứng tâm O biến: 

 ${Đ}_O( B) = D; {Đ}_O ( E) = F:\hspace{0.17em} {Đ}_O( C) = A; {Đ}_O\left(O\right)= O; {Đ}_O\left(D\right) = B$

Ba phương án A, B, C đều sai về hướng của vecto

Đáp án D

Phép đối xứng tâm O biến M(x;y) thành M’(-x;-y).

Áp dụng biểu thức tọa độ của  phép đối xứng tâm ta  có:

Chọn đáp án B

Phép đối xứng tâm I biến điểm M thành điểm M'  thì điểm I là trung  điểm của MM'.
Do đó: 

Lấy M(x;y) thuộc d, phép đối xứng tâm I (x0; y0) biến M(x; y) thành M'(x'; y') thuộc d'

Suy ra,  I là trung điểm của MM'. Do đó: 

   (1) 

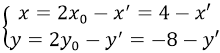
Vì điểm M(x, y) thuộc  đường thẳng d nên :  2x - 6y +  5 =  0   (2) 

Thay (1) vào (2) ta được :

2(4 - x') - 6(-8 - y') + 5 = 0 ⇒ 2x' - 6y' - 61 = 0

Suy ra,phương trình đường thẳng d' là:   2x - 6y - 61 = 0.

Chọn đáp án B

Hình bình hành có tâm đối xứng; hình tam giác cân và hình tam giác đều chỉ có trục đối xứng.

Đáp án B

Đáp án A.

Hình chữ nhật có 1 tâm đối xứng là giao điểm của 2 đường chéo

Do đó, có duy nhất một phép đối xứng tâm biến hình chữ nhật thành chính nó.

Đáp án C

Phép đối xứng tâm I biến điểm M(x;y) thành điểm M'(x'; y') nên I là  trung điểm của đoạn thẳng MM '

Đáp án D

Đáp án C

Thay tọa độ điểm I  vào phương trình đường thẳng d  ta được: 

 6. 2 + 5. (-1) - 7 = 0

Suy ra,điểm I  nằm trên đường thẳng d 

Vì tâm đối xứng I thuộc d thì phép đối xứng tâm I biến d thành chính nó.

Nhận xét: lưu ý kiểm tra xem tâm có thuộc d không, cũng như với phép tịnh tiến thì kiểm tra xem vecto tịnh tiến có cùng phương với vecto chỉ phương của d không.

Đáp án B

Hai đường thẳng d và d’ song song.

+  Xét phương án A  và B : vì điểm A(1; 2) thuộc d và điểm B(-4; 0) thuộc d’ nên A  và B  bị loại

+ Xét phương án C: điểm C ( 0;  19/10)

Tính khoảng cách từ C tới hai đường thẳng d, d’

⇒ d(C;d)=d(C;d')=> C là tâm đối xứng của hình 

Nhận xét: nếu I là tâm đối xứng của hình gồm hai đường thẳng song song thì I cách đều hai đường thẳng song song đó.

Đáp án C

Đường thẳng d vó vecto chỉ phương $\overrightarrow{u}=\left(5;3\right)$; Đường thẳng d’ có vecto chỉ phương $\overrightarrow{v}(-3;1)$ nên d không song song với d’. Tâm đối xứng của hình (H) chính là giao điểm của d và d’:

Gọi I là giao điểm của d và d’.

Điểm I thuộc d’ nên tọa độ I(2- 3t;  4+ t)

Lại có, I thuộc d nên thay tọa độ điểm I vào phương trình đường thẳng d ta được: 

    3(2 - 3t) - 5(4 + t) + 7 = 0 ⇒ -14t = 7

$\Rightarrow t=\frac{-1}{2}\Rightarrow I\left(\frac{7}{2};\frac{7}{2}\right)$

Đáp án C

Đường tròn (C) có tâm I(2; -4), bán kính  R= 3

Đường tròn (C’) có tâm J( 3; -3) và bán kính R’  = 3

Vì R=  R’ nên tồn tại phép  đối xứng tâm: biến đường tròn (C) thành (C’).

Khi đó; tâm đối xứng K là trung điểm IJ.

$\left\{\begin{array}{c}{x}_K=\frac{2+\text{}3}{2}=\frac{5}{2}\\ y_K=\frac{(-4)+\text{}(-3)}{2}=\frac{-7}{2}\end{array}\right.$

$\Rightarrow K\left(\frac{5}{2}; -\frac{7}{2}\right)$

Đáp án D

Phép đối xứng tâm I(1; 2) biến đường  tròn (C) thành đường tròn  (C')

 và biến M(x; y) thuộc (C) thành M’(x’; y’) thuộc (C') thì:

(1)

Vì điểm M(x, y) thuộc (C) nên: 

$x^2 +\hspace{0.17em} y^2+2x - 6y+\hspace{0.17em} 6 = 0$  (2) 

Thay (1) vào (2)  ta được:

${\left(2 - x\text{'}\right)}^2 + {\left(4 - y\text{'}\right)}^2 + 2(2 - x\text{'} ) - 6(4 - y\text{'} ) + 6 = 0$

⇒ $x{\text{'}}^2 + y{\text{'}}^2 - 6x\text{'} - 2y\text{'} + 6 = 0$

Suy ra phương trình (C')  $x^2 + y^2 - 6x - 2y + 6 = 0$

Đáp án A

Đáp án D

Đáp án C

Phép đối xứng tâm I biến M(x; y) thành M’(x’; y’) thì:

Thay vào phương trình (P) ta được:

$-6 - y\text{'} = {\left(8 - x\text{'}\right)}^2 - 3(8 - x\text{'}) + 1$

⇒ $-y\text{'} = x{\text{'}}^2 - 13x\text{'} + 47$ hay

$y = -x^2 + 13x - 47$

Đáp án A

Dễ thấy d // d’, ta có d ∩ Oy = A(0; 1); d’ ∩ Oy = A’(0; -4). Phép đối xứng tâm I biến Oy thành Oy thì I thuộc trục Oy; biến d thành d’ thì I là trung điểm của AA’ ⇒ I(0; -3/2).

Đáp án D