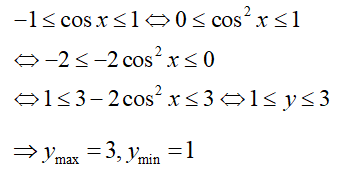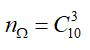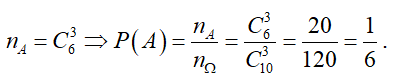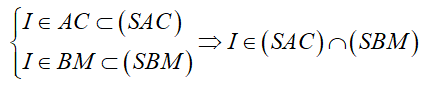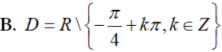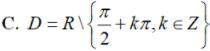Bộ 4 Đề thi Học kì 1 Toán lớp 11 năm 2020 - 2021 có đáp án (Đề 1)
53 người thi tuần này 5.0 11.8 K lượt thi 24 câu hỏi 90 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 3
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 2
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 1
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 2
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 1
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
A. = 3, = 1
B. = 1, = -1
C. = 5, = 1
D. = 5, = -1
Lời giải
Ta có:
Lời giải
Chọn D
Số phần tử của không gian mẫu:
Gọi A: “3 bạn được chọn toàn nam”.
Khi đó,
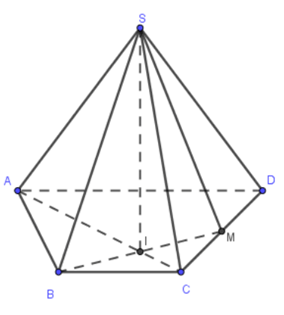
Câu 3
A. SP (P là giao điểm của AB và CD).
B. SO (O là giao điểm của AC và BD)
C. SJ (J là giao điểm của AM và BD)
D. SI (I là giao điểm của AC và BM)
Lời giải
Chọn D
Trong (ABCD), gọi I là giao điểm của AC và BM
Khi đó:
Mà 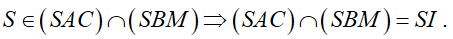
Câu 4
A. (C'):(x + 1) + (y + 2) = 4
B. (C'):(x + 1) + (y - 2) = 4
C. (C'):(x - 1) + (y - 2) = 4
D. (C'):(x - 1) + (y - 2) = 2
Lời giải
Chọn C
+ Đường tròn (C ): (x-1) + (y + 2) = 4 có tâm I( 1; -2), bán kính R = 2
+ Qua phép đối xứng trục Ox, biến tâm I (1; -2) thành tâm I’ (1; 2); bán kính R’ = R= 2.
Do đó. ảnh của đường tròn (C )qua phép đối xứng trục Ox là:
(C'): (x-1) + (y - 2) = 4
Lời giải
Chọn A
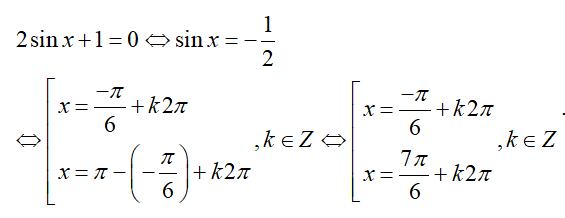
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. - 21
B. 23
C. – 17
D.- 19
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. M'(-0,5;1)
B. M'(0,5;1)
C. M'(2;-4)
D. M'(-2;4)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. “Phép vị tự tỉ số k = -1 là phép dời hình”.
B. “Phép đối xứng tâm biến đường tròn thành đường tròn có cùng bán kính”
C. “Phép đối xứng trục biến đường thẳng thành đường thẳng song song với nó”
D. “Phép quay tâm I góc quay 90° biến đường thẳng thành đường thẳng vuông góc với nó.”
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A. Tam giác MNE
B. Hình thang MNEF với F là điểm trên cạnh BD mà EF// BC
C. Tứ giác MNEF với F là điểm bất kì trên cạnh BD
D. Hình bình hành MNEF với F là điểm trên cạnh BD mà EF// BC
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
A. 4
B. 3
C. 5
D. 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
A. Nếu hai mặt phẳng 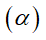
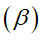
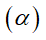
B. Nếu hai đường thẳng song song với nhau lần lượt nằm trong hai mặt phẳng phân biệt 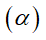
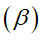
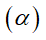
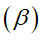
C. Qua một điểm nằm ngoài mặt phẳng cho trước ta vẽ được một và chỉ một đường thẳng song song với mặt phẳng cho trước đó
D. Nếu hai mặt phẳng 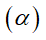
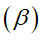
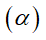
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
A. IJ // (SCD)
B. IJ // (SBD)
C. IJ // (SBC)
D. IJ // (SBM)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.