✕

✨ Đăng kí VIP để truy cập không giới hạn. Đăng ký ngay

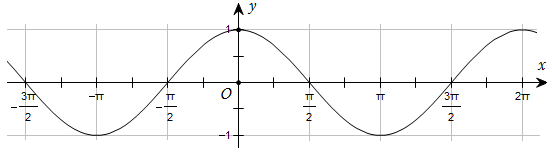
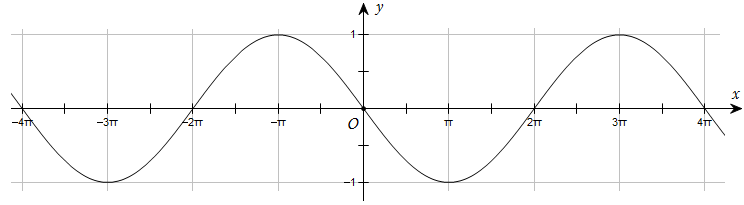
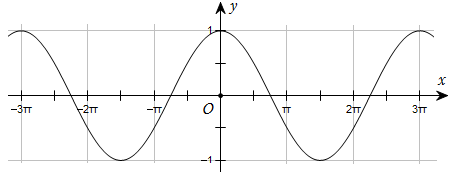
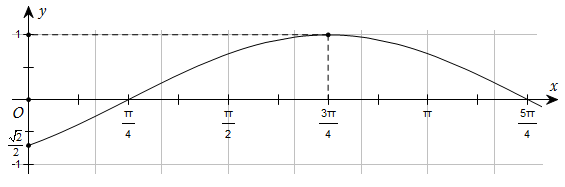
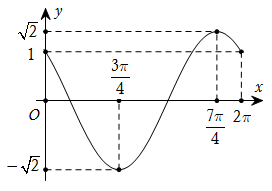
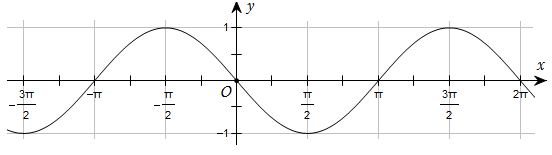
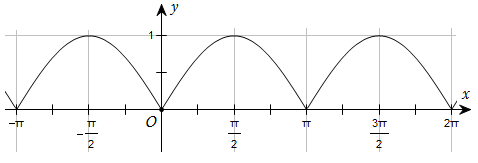
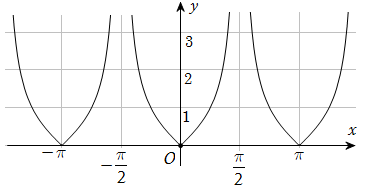
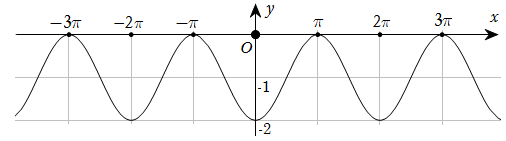
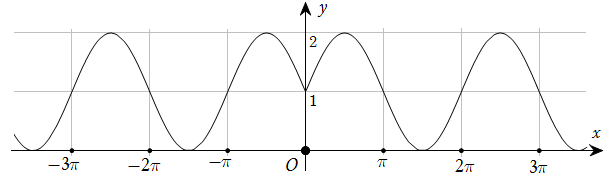
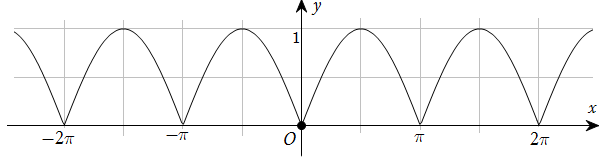
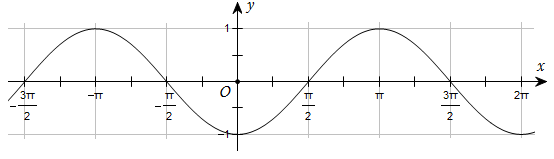184 câu Trắc nghiệm Toán 11 Bài 1: Hàm số lượng giác có đáp án (Mới nhất)

76 người thi tuần này 4.6 6.5 K lượt thi 184 câu hỏi 45 phút

Đề số 1

🔥 Đề thi HOT:

4135 người thi tuần này

Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)

55.3 K lượt thi 30 câu hỏi

1349 người thi tuần này

Bài tập Giới hạn cơ bản, nâng cao có lời giải (P1)

17.3 K lượt thi 25 câu hỏi

420 người thi tuần này

Bài tập Lượng giác lớp 11 cơ bản, nâng cao có lời giải (P1)

20.5 K lượt thi 30 câu hỏi

410 người thi tuần này

Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P3)

51.6 K lượt thi 23 câu hỏi

392 người thi tuần này

Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P2)

51.6 K lượt thi 26 câu hỏi

293 người thi tuần này

12 câu Trắc nghiệm Toán 11 Kết nối tri thức Giá trị lượng giác của góc lượng giác có đáp án

8.2 K lượt thi 12 câu hỏi

291 người thi tuần này

20 câu trắc nghiệm Toán 11 Kết nối tri thức Mẫu số liệu ghép nhóm có đáp án

3 K lượt thi 20 câu hỏi

228 người thi tuần này

20 câu Trắc nghiệm Toán 11 Cánh diều Bài 4. Hai mặt phẳng song song (Đúng-sai, trả lời ngắn) có đáp án

869 lượt thi 20 câu hỏi

Nội dung liên quan:

29 câu Trắc nghiệm Hàm số lượng giác có đáp án

lượt thi

1 đề

15 câu Trắc nghiệm Hàm số lượng giác có đáp án (Nhận biết)

lượt thi

1 đề

15 câu Trắc nghiệm Hàm số lượng giác có đáp án (Thông hiểu)

lượt thi

1 đề

10 câu Trắc nghiệm Hàm số lượng giác có đáp án (Vận dụng)

lượt thi

1 đề

21 câu Trắc nghiệm Hàm số lượng giác có đáp án (Phần 2)

lượt thi

1 đề

27 câu Trắc nghiệm Phương trình lượng giác cơ bản có đáp án

lượt thi

1 đề

15 câu Trắc nghiệm Phương trình lượng giác cơ bản có đáp án (Nhận biết)

lượt thi

1 đề

15 câu Trắc nghiệm Phương trình lượng giác cơ bản có đáp án (Thông hiểu)

lượt thi

1 đề

10 câu Trắc nghiệm Phương trình lượng giác cơ bản có đáp án (Vận dụng)

lượt thi

1 đề

Danh sách câu hỏi:

Câu 1

Tìm tập xác định của hàm số $y = \tan (x - \frac{π}{6})$

Xem đáp án

Lời giải

· Điều kiện: $\cos (x - \frac{π}{6}) \neq 0 \Leftrightarrow x - \frac{π}{6} \neq \frac{π}{2} + k π \Leftrightarrow x \neq \frac{2 π}{3} + k π$

· TXĐ: $D = ℝ \ \{\frac{2 π}{3} + k π, k \in ℤ\}$ .

Câu 2

Tìm tập xác định của hàm số $y = \cot^{2} (\frac{2 π}{3} - 3 x)$

Xem đáp án

Lời giải

· Điều kiện: $\sin (\frac{2 π}{3} - 3 x) \neq 0 \Leftrightarrow \frac{2 π}{3} - 3 x \neq k π \Leftrightarrow x \neq \frac{2 π}{9} - k \frac{π}{3}$

· TXĐ: $D = ℝ \ \{\frac{2 π}{9} + k \frac{π}{3}, k \in ℤ\}$ .

Câu 3

Tìm tập xác định của hàm số $y = \frac{\tan 2 x}{\sin x + 1} + \cot (3 x + \frac{π}{6})$

Xem đáp án

Lời giải

· Điều kiện: $\{\begin{cases} \sin x \neq - 1 \\ \sin (3 x + \frac{π}{6}) \neq 0 \end{cases} \Leftrightarrow \{\begin{cases} x \neq - \frac{π}{2} + k 2 π \\ x \neq - \frac{π}{18} + \frac{k π}{3} \end{cases}$

· Vậy TXĐ: $D = ℝ \ \{- \frac{π}{2} + k 2 π, - \frac{π}{18} + \frac{k π}{3}; k \in ℤ\}$

Câu 4

Tìm tập xác định của hàm số $y = \frac{\tan 5 x}{\sin 4 x - \cos 3 x}$

Xem đáp án

Lời giải

· Ta có: $\sin 4 x - \cos 3 x = \sin 4 x - \sin (\frac{π}{2} - 3 x)$

$= 2 \cos (\frac{x}{2} + \frac{π}{4}) \sin (\frac{7 x}{2} - \frac{π}{4})$

· Điều kiện: $\{\begin{cases} \cos 5 x \neq 0 \\ \cos (\frac{x}{2} + \frac{π}{4}) \neq 0 \\ \sin (\frac{7 x}{2} + \frac{π}{4}) \neq 0 \end{cases} \Leftrightarrow \{\begin{cases} x \neq \frac{π}{10} + k \frac{π}{5} \\ x \neq \frac{π}{2} + k 2 π \\ x \neq - \frac{π}{14} + \frac{k 2 π}{7} \end{cases}$

· Vậy TXĐ: $D = ℝ \ \{\frac{π}{10} + \frac{k π}{5}; \frac{π}{2} + k 2 π, - \frac{π}{14} + \frac{k 2 π}{7}\}$ .

Câu 5

Xét tính tuần hoàn và tìm chu kì (nếu có) của hàm số sau: $y = \cos^{2} x - 1$ .

Xem đáp án

Lời giải

Ta biến đổi: $y = \cos^{2} x - 1 = \frac{1 + \cos 2 x}{2} - 1 = \frac{1}{2} \cos 2 x - \frac{1}{2} .$

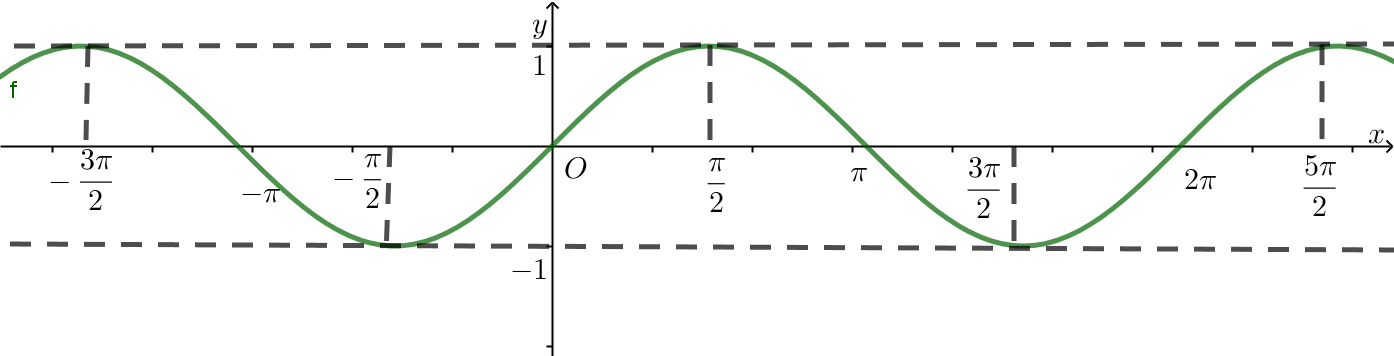
Do đó f là hàm số tuần hoàn với chu kì $Τ = \frac{2 π}{2} = π$ .

Câu 6

Xét tính tuần hoàn và tìm chu kì (nếu có) của hàm số sau: $y = \sin (\frac{2}{5} x) . \cos (\frac{2}{5} x)$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Xét tính tuần hoàn và tìm chu kì (nếu có) của hàm số sau: $y = \cos x + \cos (\sqrt{3} . x)$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8

Chứng minh rằng hàm số sau là hàm số tuần hoàn và tìm chu kì của nó: $y = \frac{1}{\sin x}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9

Xét tính chẵn, lẻ của hàm số $y = f (x) = \sin (2 x + \frac{9 π}{2})$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10

Xét tính chẵn, lẻ của hàm số $y = f (x) = \tan x + \cot x$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11

Xét tính chẵn lẻ của hàm số $y = \tan^{7} 2 x . \sin 5 x$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 12

Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau $y = 4 \sin x \cos x + 1$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 13

Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau $y = 4 - 3 \sin^{2} 2 x$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 14

Tìm giá trị lớn nhất của hàm số sau $y = \sin x - \frac{1}{\sin x}$ trong khoảng $0 < x < π$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 15

Tìm tập xác định của hàm số $y = \frac{1 - 2 x}{\sin 2 x}$ .

A. $D = ℝ \ \{k π, k \in ℤ\}$

B. $D = ℝ \ \{\frac{π}{2} + k 2 π, k 2 π, k \in ℤ\}$ .

C. $D = ℝ \ \{\frac{π}{2} + k π, k \in ℤ\}$ .

D. $D = ℝ \ \{k \frac{π}{2}, k \in ℤ\}$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 16

Tìm tập xác định của hàm số $y = \frac{3}{\cos x + 1}$

A. $D = ℝ \ \{\frac{π}{2} + k 2 π, k \in ℤ\}$ .

B. $D = ℝ \ \{k 2 π, k \in ℤ\}$ .

C. $D = ℝ \ \{π + k 2 π, k \in ℤ\}$ .

D. $D = ℝ \ \{π + k π, k \in ℤ\}$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 17

Tập xác định của hàm số $y = \sqrt{\sin x - 1}$ là

A. $ℝ$ .

B. $\{k π | k \in ℤ\}$ .

C. $\{\frac{π}{2} + k 2 π | k \in ℤ\}$ .

D. $\{\frac{π}{2} + k π | k \in ℤ\}$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 18

Tìm tập xác định D của hàm số $y = \frac{1}{\sqrt{1 - \sin x}}$ .

A. $D = ℝ \ \{k 2 π, k \in ℤ\}$ .

B. $D = ℝ \ \{π + k 2 π, k \in ℤ\}$ .

C. $D = ℝ \ \{\frac{π}{2} + k 2 π, k \in ℤ\}$ .

D. $D = ℝ \ \{- \frac{π}{2} + k 2 π, k \in ℤ\}$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 19

Tập xác định D của hàm số $y = \tan 3 x$ là

A. $D = ℝ \ \{\frac{k π}{3}, k \in ℤ\}$ .

B. $D = ℝ \ \{\frac{π}{6} + \frac{k π}{3}, k \in ℤ\}$ .

C. $D = ℝ \ \{k π, k \in ℤ\}$ .

D. $D = ℝ \ \{\frac{π}{2} + k π, k \in ℤ\}$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 20

Tìm tập xác định của hàm số $y = \frac{\tan x}{\sin x - 1}$

A. $ℝ .$

B. $ℝ \ \{\frac{π}{2} + k 2 π, k \in ℤ\}$ .

C. $ℝ \ \{\frac{π}{2} + k π, k \in ℤ\}$ .

D. $ℝ \ \{k π, k \in ℤ\}$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 21

Tập xác định của hàm số $y = \tan (2 x + \frac{π}{6})$ là

A. $ℝ \ \{\frac{π}{2} + k π, k \in ℤ\}$ .

B. $ℝ \ \{\frac{- π}{6} + \frac{k π}{2}, k \in ℤ\}$ .

C. $ℝ \ \{\frac{π}{6} + k π, k \in ℤ\}$ .

D. $ℝ \ \{\frac{π}{6} + \frac{k π}{2}, k \in ℤ\}$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 22

Tìm tập xác định của hàm số $y = \sqrt{1 - \cos x} + \cot x$ .

A. $ℝ \ \{k π, k \in ℤ\}$ .

B. $(- \infty; 1]$ .

C. $ℝ \ \{\frac{π}{2} + k π, k \in ℤ\}$ .

D. $[- 1; 1] \ \{0\}$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 23

Hàm số $y = \sqrt{\frac{\sin x - 1}{3 + \sin x}}$ có tập xác định là

A. $ℝ \ \{\frac{π}{2} + k 2 π | k \in ℤ\}$

B. $ℝ$ .

C. $\emptyset$ .

D. $\{\frac{π}{2} + k 2 π | k \in ℤ\}$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 24

Tìm tập xác định của hàm số $y = \sqrt{\frac{1 + \cos x}{1 - \sin x}}$ .

A. $ℝ \ \{k π | k \in ℤ\}$ .

B. $ℝ \ \{\frac{π}{2} + k 2 π | k \in ℤ\}$ .

C. $ℝ$ .

D. $ℝ \ \{k 2 π | k \in ℤ\}$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 25

Tập xác định của hàm số $y = \frac{\cot x}{\cos x - 1}$ là

A. $ℝ \ \{k \frac{π}{2}, k \in ℤ\}$ .

B. $ℝ \ \{\frac{π}{2} + k π, k \in ℤ\}$ .

C. $ℝ \ \{k π, k \in ℤ\}$ .

D. $ℝ \ \{k 2 π, k \in ℤ\}$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 26

Tập xác định của hàm số $f (x) = \frac{1}{1 - \cos x}$ là

A. $ℝ \ \{(2 k + 1) \frac{π}{2} |k \in ℤ\}$ .

B. $ℝ \ \{(2 k + 1) π |k \in ℤ\}$ .

C. $ℝ \ \{k π |k \in ℤ\}$ .

D. $ℝ \ \{k 2 π |k \in ℤ\}$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 27

Tìm tập xác định D của hàm số $y = \frac{1}{\sin (x - \frac{π}{2})}$

A. $D = R \ \{(2 k + 1) π, k \in ℤ\}$

B. $D = R \ \{\frac{k π}{2}, k \in ℤ\}$

C. $D = R \ \{(2 k + 1) \frac{π}{2}, k \in ℤ\}$

D.

D = R \ \{k π, k \in ℤ\}

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 28

Hàm số $y = \frac{\tan 2 x}{1 - \tan x}$ có tập xác định là

A. $ℝ$ .

B. $ℝ \ \{\frac{π}{4} + k \frac{π}{2} | k \in ℤ\}$ .

C. $ℝ \ \{\frac{π}{2} + k π | k \in ℤ\}$ .

D. $ℝ \ \{\frac{π}{4} + k \frac{π}{2}, \frac{π}{2} + k π | k \in ℤ\}$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 29

Tập xác định của hàm số $y = \frac{3 + \cot \frac{x}{2}}{\cos x + 1}$ là:

A. $ℝ \ \{k π |k \in ℤ\} .$

B. $ℝ \ \{k 2 π |k \in ℤ\} .$

C. $ℝ \ \{π + k 2 π |k \in ℤ\} .$

D.

ℝ \ \{\frac{π}{2} + k 2 π |k \in ℤ\} .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 30

Cho các hàm số

$(1) y = \sin 3 x . (2) y = \frac{\tan x + 3}{\cos^{2} x + 2} . (3) y = \frac{2 \cos x - 1}{\sin^{2} x + 1}$

$(4) y = \sqrt{1 - \sin x} . (5) y = \sqrt{\frac{2 \cos x + 3}{\sin x + 1}} .$

Trong các hàm số trên có bao nhiêu hàm số có tập xác định là $ℝ$

A.4 .

B. 1 .

C. 3 .

D. 2

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 31

Tập xác định của hàm số $y = \frac{\cos x - 2}{1 + \sin x}$ là

A. $ℝ \ \{k π | k \in ℤ\}$ .

B. $ℝ \ \{- \frac{π}{2} + k π | k \in ℤ\}$ .

C. $ℝ \ \{k 2 π | k \in ℤ\}$ .

D. $ℝ \ \{- \frac{π}{2} + k 2 π | k \in ℤ\}$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 32

Tập xác định của hàm số $y = \frac{1}{\sqrt{s inx + 1}}$ là

A. $ℝ \ \{\frac{π}{2} + k 2 π, k \in ℤ\}$ .

B. $ℝ \ \{- \frac{π}{2} + k 2 π, k \in ℤ\}$ .

C. $ℝ \ \{- \frac{π}{2} + k π, k \in ℤ\}$ .

D. $ℝ$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 33

Tập xác định của hàm số $y = \frac{s inx + 1}{s inx - 2}$ là

A. $(- 2; + \infty)$

B. $(2; + \infty)$

C. $ℝ \ \{2\}$ .

D. $ℝ$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 34

Hàm số $y = \frac{2 \sin x + 1}{1 - \cos x}$ xác định khi

A. $x \neq \frac{π}{2} + k 2 π$ .

B. $x \neq k π$ .

C. $x \neq k 2 π$ .

D.

x \neq \frac{π}{2} + k π

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 35

Trong các mệnh đề sau, mệnh đề nào đúng?

A. Các hàm số $y = \sin x, y = \cos x, y = \cot x$ đều là hàm số chẵn.

B. Các hàm số $y = \sin x, y = \cot x, y = \tan x$ đều là hàm số lẻ.

C. Các hàm số $y = \sin x, y = \cot x, y = \tan x$ đều là hàm số chẵn.

D. Các hàm số $y = \sin x, y = \cos x, y = \cot x$ đều là hàm số lẻ.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 36

Hàm số nào sau đây là hàm số chẵn?

A. y= cot 4x .

B. $y = \tan 6 x$ .

C. $y = \sin 2 x$ .

D. $y = \cos x$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 37

Trong các hàm số sau đây, hàm số nào có đồ thị đối xứng qua trục tung?

A. $y = \tan x$ .

B. $y = \cos x$ .

C. $y = \sin x$ .

D. $y = \cot x$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 38

Trong các hàm số sau, hàm số nào là hàm số chẵn?

A. $y = \cos x$ .

B. $y = \tan x$ .

C. $y = s i n x$ .

D. $y = \cot x$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 39

Trong các hàm số sau, hàm số nào là hàm số lẻ?

A. $y = 1 + \sin x$ .

B. $y = x . \tan x$ .

C. $y = \sin^{5} x$ .

D. $y = \cos x . \sin^{2} x$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 40

Hàm số nào sau đây là hàm số chẵn?

A. $y = - 2 \sin x$ .

B. $y = 2 \sin 2 x$ .

C. $y = \sin x - \cos x$ .

D. $y = - 2 \cos x$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 41

Trong các hàm số sau, hàm số nào là hàm số chẵn trên $ℝ$ ?

A. $y = \sin (\frac{π}{2} - x)$ .

B. $y = \tan x$ .

C.

y = \sin x

.

D.

y = \sin (x + \frac{π}{6})

.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 42

Cho hàm số $y = \frac{1}{\cos x}$ . Phát biểu nào sau đây đúng?

A. Hàm số có tập xác định là $ℝ \ \{0\}$ .

B. Đồ thị của hàm số nhận trục tung làm trục đối xứng.

C. Hàm số đó là hàm số lẻ trên $D = ℝ \ \{\frac{π}{2} + k π, k \in ℤ\}$ .

D. Hàm số đó là hàm số lẻ trên $ℝ$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 43

Trong các hàm số sau, hàm số nào là hàm số lẻ?

A. $y = x^{2} \cos x$ .

B. $y = \sin 2 x$ .

C. $y = \sin^{2} x$ .

D. $y = \cos 2 x$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 44

Trong các hàm số sau, hàm số nào không là hàm số chẵn và cũng không là hàm số lẻ?

A. $y = \sin (x + \frac{π}{4}) + \tan (x + \frac{π}{4})$ .

B. $y = \tan x - \frac{1}{\sin x}$ .

C. $y = \sin^{4} x - \cos^{4} x$ .

D.

y = \cos x

.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 45

Hàm số nào sau đây là hàm số chẵn.

A. $y = \cot x$ .

B. $y = \sin x$ .

C. $y = \tan x$ .

D. $y = \cos x$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 46

Trong các hàm số sau, hàm số nào là hàm chẵn?

A. $y = \cos (x + \frac{π}{3})$ .

B.

y = |\sin x|

.

C.

y = 1 - \sin x

.

D.

y = \sin x + \cos x

.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 47

Trong các hàm số sau, hàm số nào là hàm số chẵn?

A. $y = \tan x$ .

B. $y = \sin x$ .

C. $y = \cos x$ .

D. $y = \cot x$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 48

Hàm số nào sau đây là hàm số tuần hoàn với chu kỳ $T = π$ ?

A. $y = \sin x$ .

B. $y = 2 \sin x$ .

C. $y = \sin 2 x$ .

D. $y = 2 + \sin x$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 49

Hàm số nào sau đây tuần hoàn với chu kì $T = \frac{π}{2}$ ?

A. $y = \tan \frac{x}{3}$ .

B. $y = \tan \frac{x}{2}$ .

C. $y = \tan 3 x$ .

D. $y = \tan 2 x$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 50

Chọn khẳng định sai?

A. Hàm số $y = \tan x + \sin x$ là hàm số tuần hoàn với chu kì $2 π .$

B. Hàm số $y = \cos x$ là hàm số tuần hoàn với chu kì $2 π .$

C. Hàm số $y = \cot x + \tan x$ là hàm số tuần hoàn với chu kì $π .$

D. Hàm số $y = \sin x$ là hàm số tuần hoàn với chu kì $π$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 51

Chu kỳ tuần hoàn của hàm số $y = \cot (3 x + \frac{π}{6})$ là

A. $π$ .

B. $\frac{2 π}{3}$ .

C. $\frac{π}{3}$ .

D. $2 π$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 52

Khẳng định nào sau đây đúng?

A. Hàm số $y = \sin x$ tuần hoàn với chu kì $π$ .

B. Hàm số $y = \tan x$ tuần hoàn với chu kì $2 π$ .

C. Hàm số $y = \cos x$ tuần hoàn với chu kì $\frac{π}{2}$ .

D. Hàm số $y = \cot x$ tuần hoàn với chu kì $π$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 53

Trong bốn hàm số: $(1) y = \cos 2 x; (2) y = \sin x; (3) y = \tan 2 x; (4) y = \cot 4 x$ có mấy hàm số tuần hoàn với chu kỳ $π$ ?

A. 3.

B. 2.

C. 0.

D. 1.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 54

Khẳng định nào sai trong các khẳng định sau?

A. $y = \cos x$ tuần hoàn với chu kỳ $π$ .

B. $y = \cos x$ là hàm nghịch biến trên $(0; π)$ .

C. $y = \cos x$ là hàm chẵn.

D.

y = \cos x

có tập xác định

ℝ

.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 55

Hàm số $y = \frac{1}{1 + \tan^{2} x} + \frac{1}{1 + \cot^{2} 2 x}$ có chu kì là:

A. $T = \frac{π}{2}$ .

B. $T = 2 π$ .

C. $T = π$ .

D. $T = 4 π$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 56

Chu kì tuần hoàn của hàm số $y = \cot x$ là

A. $π$ .

B. $2 π$ .

C. $k π$ , (

k \in ℤ

).

D. $k 2 π$ , (

k \in ℤ

).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 57

Chu kỳ tuần hoàn của hàm số $y = \tan x$ là

A. $2 π$

B. $π$

C. $\frac{π}{2}$

D.

3 π

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 58

Chu kỳ tuần hoàn của hàm số $y = \cos x$

A. $T = \frac{π}{2}$ .

B. $T = π$ .

C. $T = 2$ .

D. $T = 2 π$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 59

Giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y = 3 \cos 2 x - 5$ lần lượt là

A. $- 8$ và -2 .

B. 2 và 8 .

C. -5 và 3 .

D. -5 và 2 .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 60

Giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y = 7 - 2 \sin (x + \frac{π}{4})$ lần lượt là

A. 4 và 7.

B. 5 và 9.

C. -2 và 7.

D. -2 và 2.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 61

Tìm tập giá trị của hàm số $y = 2 \cos 3 x + 1$ .

A. $[- 3; 1]$ .

B. $[- 3; - 1]$ .

C. $[- 1; 3]$ .

D. $[1; 3]$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 62

Tổng giá trị lớn nhất và nhỏ nhất của hàm số $y = 3 \cos x + 4$ là

A. 7.

B. 5.

C. 8.

D. 6.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 63

Giá trị nhỏ nhất của hàm số: $y = 3 \sin (x + \frac{π}{4})$ là:

A. 0.

B. -3.

C. 3.

D. -1.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 64

Hàm số $y = \sin x$ có tập giá trị là:

A. $ℝ$ .

B. $[- 1; 1]$ .

C. $[- π; π]$ .

D. $[0; π]$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 65

Giá trị lớn nhất của hàm số $y = 2 \sin x + 1$ là

A. $- 1$ .

B. $1$ .

C. $- \frac{1}{2}$ .

D. $3$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 66

Giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y = 4 \sqrt{\sin x + 3} - 1$ lần lượt là

A. $\sqrt{2}$ và $2$ .

B. $4 \sqrt{2}$ và

8

.

C. $2$ và 4.

D.

4 \sqrt{2} - 1

và

7

.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 67

Giá trị lớn nhất, giá trị nhỏ nhất của hàm số $y = 2 - \cos^{2} x$ là

A. 2 và -1.

B. 2 và 0.

C. 2 và 1.

D. 3 và 1.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 68

Cho hàm số $y = \sin x$ trên đoạn $[\frac{- 3 π}{2}; \frac{5 π}{2}]$ có đồ thị như hình vẽ. Tìm những giá trị x để hàm số nhận giá trị âm.

A. .

B. .

C. .

D. .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 69

Giá trị lớn nhất, nhỏ nhất của hàm số $y = 3 - 2 \cos^{2} x$ lần lượt là

A. $y_{\max} = 5, y_{\min} = 1$ .

B.

y_{\max} = 1, y_{\min} = - 1

.

C.

y_{\max} = 3, y_{\min} = 1

.

D.

y_{\max} = 5, y_{\min} = - 1

.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 70

Tìm giá trị lớn nhất M của hàm số $y = 2 \cos x - \sin x$ .

A. $M = \sqrt{\frac{11}{2}}$ .

B. $M = \sqrt{5}$ .

C. $M = \sqrt{3}$ .

D. $M = \sqrt{6}$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 71

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \sqrt{2} \cos 2 x - 1$ trên đoạn $[- \frac{π}{6}; \frac{3 π}{8}]$ . khi đó $M . m$ bằng

A. -1.

B. $2 - 2 \sqrt{2} .$

C. $2 - \sqrt{2} .$

D.

2 \sqrt{2} - 2.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 72

Tập giá trị hàm số y= 5sinx- 12cosx là

A. $[- 12; 5]$ .

B. $[- 13; 13]$ .

C. $[- 17; 17]$ .

D. $(- 13; 13)$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 73

Hàm số $y = 4 - 11 \cos^{3} x$ có tất cả bao nhiêu giá trị nguyên dương?

A. 15.

B. 14.

C.13.

D.23.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 74

Giá trị lớn nhất của hàm số $y = 5 \sin 2 x + 12 \cos 2 x$ là

A. 10.

B. 12.

C. 17.

D. 13.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 75

Đồ thị trong hình vẽ dưới đây là của hàm số nào?

A. $y = \cot x$ .

B. $y = \sin 2 x$ .

C. $y = \sin x$ .

D. $y = \cos 2 x$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 76

Cho đồ thị với $x \in [- π; π]$ . Đây là đồ thị của hàm số của hàm số nào?

A. $y = \cos x$ .

B. $y = - \cos x$ .

C. $y = \sin x$ .

D. $y = \cos |x|$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 77

Dựa vào đồ thị của hàm số $y = \sin x$ , hãy tìm số nghiệm của phương trình: $\sin x = \frac{1}{2018}$ trên đoạn $[\frac{- 5 π}{2}; \frac{5 π}{2}]$ .

A. 4.

B. 6.

C. 10.

D. 5.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 78

Hình bên là một phần đồ thị của hàm số nào sau đây?

A. $y = \cos \frac{2 x}{3}$ .

B. $y = \sin \frac{2 x}{3}$ .

C. $y = \cos \frac{3 x}{2}$

D. $y = \sin \frac{3 x}{2}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 79

Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C,D.

Hỏi hàm số đó là hàm số nào?

A. $y = \sin \frac{3 x}{2} .$

B. $y = \sin \frac{2 x}{3} .$

C. $y = cos \frac{3 x}{2} .$

D. $y = cos \frac{2 x}{3} .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 80

Tìm mệnh đề sai trong các mệnh đề sau.

A. Hàm số $y = \cos x$ tuần hoàn với chu kì $2 π$ .

B. Hàm số $y = \sin x$ nghịch biến trên khoảng $(\frac{π}{2}; π)$ .

C. Hàm số $y = \cot x$ đồng biến trên khoảng $(\frac{π}{2}; π)$ .

D. Hàm số $y = \tan x$ tuần hoàn với chu kì $π$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 81

Hàm số $y = \tan x$ đồng biến trên khoảng nào dưới đây?

A. $(0; π)$ .

B. $(- \frac{3 π}{2}; - \frac{π}{2})$ .

C. $(- \frac{3 π}{2}; \frac{π}{2})$

D. $(- 2 π; - π)$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 82

Tìm mệnh đề đúng trong các mệnh đề sau?

A. Hàm số $y = \cot x$ đồng biến trên khoảng $(0; π)$ .

B. Hàm số $y = \sin x$ đồng biến trên khoảng $(\frac{3 π}{2}; \frac{5 π}{2})$ .

C. Hàm số $y = \sin x$ nghịch biến trên khoảng $(π; 2 π)$ .

D. Hàm số $y = \cos x$ đồng biến trên khoảng $(- \frac{π}{2}; \frac{π}{2})$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 83

Cho hàm số $y = \sin x$ . Khẳng định nào dưới đây sai?

A. Hàm số đã cho là hàm lẻ.

B. Hàm số đã cho có tập giá trị là $[- 1; 1]$ .

C. Hàm số đã cho đồng biến trên $(0; 2 π)$ .

D. Hàm số đã cho có tập xác định

ℝ

.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 84

Cho ba hàm số $y = s in x; y = cos x; y = tan x$ . Có bao nhiêu hàm số đồng biến trên $(0; \frac{3 π}{2})$ ?

A. 1.

B. 3.

C. 0.

D. 2.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 85

Tìm tập xác định D của hàm số $y = \frac{2019}{\sin x} .$

A. $D = ℝ .$

B. $D = ℝ \ \{0\} .$

C.

D = ℝ \ \{k π, k \in ℤ\} .

D.

D = ℝ \ \{\frac{π}{2} + k π, k \in ℤ\} .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 86

Tìm tập xác định D của hàm số $y = \frac{1 - \sin x}{\cos x - 1} .$

A. $D = ℝ .$

B. $D = ℝ \ \{\frac{π}{2} + k π, k \in ℤ\} .$

C. $D = ℝ \ \{k π, k \in ℤ\} .$

D.

D = ℝ \ \{k 2 π, k \in ℤ\} .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 87

Tìm tập xác định D của hàm số $y = \frac{1}{\sin (x - \frac{π}{2})} .$

A. $D = ℝ \ \{k \frac{π}{2}, k \in ℤ\} .$

B. $D = ℝ \ \{k π, k \in ℤ\} .$

C. $D = ℝ \ \{(1 + 2 k) \frac{π}{2}, k \in ℤ\} .$

D.

D = ℝ \ \{(1 + 2 k) π, k \in ℤ\} .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 88

Tìm tập xác định D của hàm số $y = \frac{1}{\sin x - \cos x} .$

A. $D = ℝ .$

B. $D = ℝ \ \{- \frac{π}{4} + k π, k \in ℤ\} .$

C. $D = ℝ \ \{\frac{π}{4} + k 2 π, k \in ℤ\} .$

D. $D = ℝ \ \{\frac{π}{4} + k π, k \in ℤ\} .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 89

Hàm số $y = \tan x + \cot x + \frac{1}{\sin x} + \frac{1}{\cos x}$ không xác định trong khoảng nào trong các khoảng sau đây?

A. $(k 2 π; \frac{π}{2} + k 2 π)$ với $k \in ℤ .$

B. $(π + k 2 π; \frac{3 π}{2} + k 2 π)$ với $k \in ℤ .$

C. $(\frac{π}{2} + k 2 π; π + k 2 π)$ với $k \in ℤ .$

D.

(π + k 2 π; 2 π + k 2 π)

với

k \in ℤ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 90

Tìm tập xác định D của hàm số $y = \cot (2 x - \frac{π}{4}) + \sin 2 x .$

A. $D = ℝ \ \{\frac{π}{4} + k π, k \in ℤ\} .$

B. $D = \emptyset .$

C. $D = ℝ \ \{\frac{π}{8} + k \frac{π}{2}, k \in ℤ\} .$

D. $D = ℝ .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 91

Tìm tập xác định D của hàm số $y = 3 \tan^{2} (\frac{x}{2} - \frac{π}{4}) .$

A. $D = ℝ \ \{\frac{3 π}{2} + k 2 π, k \in ℤ\} .$

B. $D = ℝ \ \{\frac{π}{2} + k 2 π, k \in ℤ\} .$

C. $D = ℝ \ \{\frac{3 π}{2} + k π, k \in ℤ\} .$

D. $D = ℝ \ \{\frac{π}{2} + k π, k \in ℤ\} .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 92

Hàm số $y = \frac{\cos 2 x}{1 + \tan x}$ không xác định trong khoảng nào trong các khoảng sau đây?

A. $(\frac{π}{2} + k 2 π; \frac{3 π}{4} + k 2 π)$ với $k \in ℤ .$

B. $(- \frac{π}{2} + k 2 π; \frac{π}{2} + k 2 π)$ với $k \in ℤ .$

C. $(\frac{3 π}{4} + k 2 π; \frac{3 π}{2} + k 2 π)$ với $k \in ℤ .$

D.

(π + k 2 π; \frac{3 π}{2} + k 2 π)

với

k \in ℤ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 93

Tìm tập xác định D của hàm số $y = \frac{3 \tan x - 5}{1 - \sin^{2} x} .$

A. $D = ℝ \ \{\frac{π}{2} + k 2 π, k \in ℤ\} .$

B. $D = ℝ \ \{\frac{π}{2} + k π, k \in ℤ\} .$

C. $D = ℝ \ \{π + k π, k \in ℤ\} .$

D. $\cos x \neq \pm 1 \Leftrightarrow \sin x \neq 0 \Leftrightarrow x \neq k π, k \in ℤ .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 94

Tìm tập xác định D của hàm số $y = \sqrt{\sin x + 2} .$

A. $D = ℝ .$

B.

D = [- 2; + \infty) .

C.

D = [0; 2 π] .

D. $D = \emptyset .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 95

Tìm tập xác định D của hàm số $y = \sqrt{\sin x - 2} .$

A. $D = ℝ .$

B.

ℝ \ \{k π, k \in ℤ\} .

C.

D = [- 1; 1] .

D. $D = \emptyset .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 96

Tìm tập xác định $D$ của hàm số $y = \frac{1}{\sqrt{1 - \sin x}} .$

A. $D = ℝ \ \{k π, k \in ℤ\} .$

B. $D = ℝ \ \{\frac{π}{2} + k π, k \in ℤ\} .$

C. $D = ℝ \ \{\frac{π}{2} + k 2 π, k \in ℤ\} .$

D. $D = \emptyset .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 97

Tìm tập xác định D của hàm số $y = \sqrt{1 - \sin 2 x} - \sqrt{1 + \sin 2 x} .$

A. $D = \emptyset .$

B. $D = ℝ .$

C. $D = [\frac{π}{6} + k 2 π; \frac{5 π}{6} + k 2 π], k \in ℤ .$

D.

D = [\frac{5 π}{6} + k 2 π; \frac{13 π}{6} + k 2 π], k \in ℤ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 98

Tìm tập xác định D của hàm số $y = \sqrt{5 + 2 \cot^{2} x - \sin x} + \cot (\frac{π}{2} + x) .$

A. $D = ℝ \ \{\frac{k π}{2}, k \in ℤ\} .$

B. $D = ℝ \ \{- \frac{π}{2} + k π, k \in ℤ\} .$

C. $D = ℝ .$

D.

D = ℝ \ \{k π, k \in ℤ\} .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 99

Tìm tập xác định D của hàm số $y = \tan (\frac{π}{2} \cos x) .$

A. $D = ℝ \ \{\frac{π}{2} + k π, k \in ℤ\}$ .

B. $D = ℝ \ \{\frac{π}{2} + k 2 π, k \in ℤ\}$ .

C. $D = ℝ$ .

D. $D = ℝ \ \{k π, k \in ℤ\}$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 100

Trong các hàm số sau, hàm số nào là hàm số chẵn?

A. $y = \sin x .$

B. $y = \cos x .$

C. $y = \tan x .$

D.

y = \cot x .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 101

Trong các hàm số sau, hàm số nào là hàm số chẵn?

A. $y = - \sin x .$

B. $y = \cos x - \sin x .$

C. $y = \cos x + \sin^{2} x .$

D. $y = \cos x \sin x .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 102

Trong các hàm số sau, hàm số nào là hàm số chẵn?

A. $y = \sin 2 x .$

B.

y = x \cos x .

C.

y = \cos x . \cot x .

D.

y = \frac{\tan x}{\sin x} .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 103

Trong các hàm số sau, hàm số nào là hàm số chẵn?

A. $y = |\sin x| .$

B.

y = x^{2} \sin x .

C. $y = \frac{x}{\cos x} .$

D.

y = x + \sin x .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 104

Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua trục tung?

A. $y = \sin x \cos 2 x .$

B. $y = \sin^{3} x . \cos (x - \frac{π}{2}) .$

C. $y = \frac{\tan x}{\tan^{2} x + 1} .$

D.

y = \cos x \sin^{3} x .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 105

Trong các hàm số sau, hàm số nào là hàm số lẻ?

A. y = cosx + sin²x.

B. y = sinx + cosx.

C. y = ‒cosx.

D. y = sinxcos3x.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 106

Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?

A. $y = \cot 4 x .$

B. $y = \frac{\sin x + 1}{\cos x} .$

C. $y = \tan^{2} x .$

D.

y = |\cot x| .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 107

Trong các hàm số sau, hàm số nào là hàm số lẻ?

A. $y = \sin (\frac{π}{2} - x) .$

B. $y = \sin^{2} x .$

C. $y = \frac{\cot x}{\cos x} .$

D. $y = \frac{\tan x}{\sin x} .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 108

Trong các hàm số sau, hàm số nào là hàm số lẻ?

A. $y = 1 - \sin^{2} x .$

B. $y = |\cot x| . \sin^{2} x .$

C. $y = x^{2} \tan 2 x - \cot x .$

D.

y = 1 + |\cot x + \tan x| .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 109

Cho hàm số $f (x) = \sin 2 x$ và $g (x) = \tan^{2} x .$ Chọn mệnh đề đúng

A. $f (x)$ là hàm số chẵn, $g (x)$ là hàm số lẻ.

B. $f (x)$ là hàm số lẻ, $g (x)$ là hàm số chẵn.

C. $f (x)$ là hàm số chẵn, $g (x)$ là hàm số chẵn.

D. $f (x)$ và $g (x)$ đều là hàm số lẻ.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 110

Cho hai hàm số $f (x) = \frac{\cos 2 x}{1 + \sin^{2} 3 x}$ và $g (x) = \frac{|\sin 2 x| - \cos 3 x}{2 + \tan^{2} x}$ . Mệnh đề nào sau đây là đúng?

A. $f (x)$ lẻ và $g (x)$ chẵn.

B. $f (x)$ và $g (x)$ chẵn.

C. $f (x)$ chẵn, $g (x)$ lẻ.

D.

f (x)

và

g (x)

lẻ.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 111

Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?

A. $y = \frac{1}{\sin^{3} x} .$

B.

y = \sin (x + \frac{π}{4}) .

C.

y = \sqrt{2} \cos (x - \frac{π}{4}) .

D.

y = \sqrt{\sin 2 x} .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 112

Mệnh đề nào sau đây là sai?

A. Đồ thị hàm số $y = |\sin x|$ đối xứng qua gốc tọa độ O

B. Đồ thị hàm số $y = \cos x$ đối xứng qua trục Oy

C. Đồ thị hàm số $y = |\tan x|$ đối xứng qua trục Oy.

D. Đồ thị hàm số $y = \tan x$ đối xứng qua gốc tọa độ O

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 113

Trong các hàm số sau, hàm số nào là hàm số chẵn?

A. $y = 2 \cos (x + \frac{π}{2}) + \sin (π - 2 x) .$

B. $y = \sin (x - \frac{π}{4}) + \sin (x + \frac{π}{4}) .$

C. $y = \sqrt{2} \sin (x + \frac{π}{4}) - \sin x .$

D.

y = \sqrt{\sin x} + \sqrt{\cos x} .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 114

Trong các hàm số sau, hàm số nào là hàm số lẻ ?

A. $y = x^{4} + \cos (x - \frac{π}{3}) .$

B. $y = x^{2017} + \cos (x - \frac{π}{2}) .$

C. $y = 2015 + \cos x + \sin^{2018} x .$

D. $y = \tan^{2017} x + \sin^{2018} x .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 115

Mệnh đề nào sau đây là sai?

A. Hàm số $y = \sin x$ tuần hoàn với chu kì $2 π .$

B. Hàm số $y = \cos x$ tuần hoàn với chu kì $2 π .$

C. Hàm số $y = \tan x$ tuần hoàn với chu kì $2 π .$

D. Hàm số $y = \cot x$ tuần hoàn với chu kì $π .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 116

Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn?

A. $y = \sin x$

B. $y = x + \sin x$

C.

y = x \cos x .

D. $y = \frac{\sin x}{x} .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 117

Trong các hàm số sau đây, hàm số nào không tuần hoàn?

A. $y = \cos x .$

B. $y = \cos 2 x .$

C. $y = x^{2} \cos x$

D. $y = \frac{1}{\sin 2 x} .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 118

Tìm chu kì T của hàm số $y = \sin (5 x - \frac{π}{4}) .$

A. $T = \frac{2 π}{5} .$

B. $T = \frac{5 π}{2} .$

C. $T = \frac{π}{2} .$

D.

T = \frac{π}{8} .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 119

Tìm chu kì T của hàm số $y = \cos (\frac{x}{2} + 2016) .$

A. $T = 4 π .$

B. $T = 2 π .$

C. $T = - 2 π .$

D. $T = π .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 120

Tìm chu kì T của hàm số $y = - \frac{1}{2} \sin (100 π x + 50 π) .$

A. $T = \frac{1}{50} .$

B.

T = \frac{1}{100} .

C.

T = \frac{π}{50} .

D.

T = 200 π^{2} .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 121

Tìm chu kì T của hàm số $y = \cos 2 x + \sin \frac{x}{2} .$

A. $T = 4 π .$

B. $T = π .$

C. $T = π .$

D. $T = \frac{π}{2} .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 122

Tìm chu kì T của hàm số $y = \cos 3 x + \cos 5 x .$

A. $T = π .$

B. $T = 3 π .$

C. $T = 2 π .$

D. $T = 5 π .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 123

Tìm chu kì T của hàm số $y = 3 \cos (2 x + 1) - 2 \sin (\frac{x}{2} - 3) .$

A. $T = 2 π .$

B.

T = 4 π

C. $T = 6 π$

D.

T = π .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 124

Tìm chu kì T của hàm số $y = \sin (2 x + \frac{π}{3}) + 2 \cos (3 x - \frac{π}{4}) .$

A. $T = 2 π .$

B. $T = π .$

C. $T = 3 π .$

D.

T = 4 π .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 125

Tìm chu kì T của hàm số $y = \tan 3 π x .$

A. $T = \frac{π}{3} .$

B. $T = \frac{4}{3} .$

C. $T = \frac{2 π}{3} .$

D. $T = \frac{1}{3} .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 126

Tìm chu kì T của hàm số $y = \tan 3 x + \cot x .$

A. $T = 4 π .$

B. $T = π .$

C. $T = 3 π .$

D. $T = \frac{π}{3} .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 127

Tìm chu kì T của hàm số $y = \cot \frac{x}{3} + \sin 2 x .$

A. $T = 4 π .$

B. $T = π .$

C. $T = 3 π .$

D. $T = \frac{π}{3} .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 128

Tìm chu kì T của hàm số $y = \sin \frac{x}{2} - \tan (2 x + \frac{π}{4}) .$

A. $T = 4 π .$

B. $T = π .$

C. $T = 3 π .$

D.

T = 2 π .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 129

Tìm chu kì T của hàm số $y = 2 \cos^{2} x + 2017.$

A. $T = 3 π .$

B. $T = 2 π .$

C.

T = π .

D.

T = 4 π .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 130

Tìm chu kì T của hàm số $y = 2 \sin^{2} x + 3 \cos^{2} 3 x .$

A. $T = π .$

B.

T = 2 π .

C.

T = 3 π .

D. $T = \frac{π}{3} .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 131

Tìm chu kì T của hàm số $y = \tan 3 x - \cos^{2} 2 x .$

A. $T = π .$

B.

T = \frac{π}{3} .

C.

T = \frac{π}{2} .

D.

T = 2 π .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 132

Hàm số nào sau đây có chu kì khác $π$ ?

A. $y = \sin (\frac{π}{3} - 2 x) .$

B. $y = \cos 2 (x + \frac{π}{4}) .$

C. $y = \tan (- 2 x + 1) .$

D.

y = \cos x \sin x .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 133

Hàm số nào sau đây có chu kì khác $2 π$ ?

A. $y = \cos^{3} x .$

B.

y = \sin \frac{x}{2} \cos \frac{x}{2} .

C.

y = \sin^{2} (x + 2) .

D.

y = \cos^{2} (\frac{x}{2} + 1) .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 134

Hai hàm số nào sau đây có chu kì khác nhau?

A. $y = \cos x$ và $y = \cot \frac{x}{2} .$

B. $y = \sin x$ và $y = \tan 2 x .$

C. $y = \sin \frac{x}{2}$ và $y = \cos \frac{x}{2} .$

D. $y = \tan 2 x$ và

y = \cot 2 x .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 135

Cho hàm số $y = \sin x$ . Mệnh đề nào sau đây là đúng?

A. Hàm số đồng biến trên khoảng $(\frac{π}{2}; π)$ , nghịch biến trên khoảng $(π; \frac{3 π}{2})$ .

B. Hàm số đồng biến trên khoảng $(- \frac{3 π}{2}; - \frac{π}{2})$ , nghịch biến trên khoảng $(- \frac{π}{2}; \frac{π}{2})$ .

C. Hàm số đồng biến trên khoảng $(0; \frac{π}{2})$ , nghịch biến trên khoảng $(- \frac{π}{2}; 0)$ .

D. Hàm số đồng biến trên khoảng $(- \frac{π}{2}; \frac{π}{2})$ , nghịch biến trên khoảng $(\frac{π}{2}; \frac{3 π}{2})$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 136

Với $x \in (\frac{31 π}{4}; \frac{33 π}{4})$ , mệnh đề nào sau đây là đúng?

A. Hàm số $y = \cot x$ nghịch biến.

B. Hàm số $y = \tan x$ nghịch biến.

C. Hàm số $y = \sin x$ đồng biến.

D. Hàm số

y = \cos x

nghịch biến.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 137

Với $x \in (0; \frac{π}{4})$ , mệnh đề nào sau đây là đúng?

A. Cả hai hàm số $y = - \sin 2 x$ và $y = - 1 + \cos 2 x$ đều nghịch biến.

B. Cả hai hàm số $y = - \sin 2 x$ và $y = - 1 + \cos 2 x$ đều đồng biến.

C. Hàm số $y = - \sin 2 x$ nghịch biến, hàm số $y = - 1 + \cos 2 x$ đồng biến.

D. Hàm số $y = - \sin 2 x$ đồng biến, hàm số $y = - 1 + \cos 2 x$ nghịch biến.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 138

Hàm số $y = \sin 2 x$ đồng biến trên khoảng nào trong các khoảng sau?

A. $(0; \frac{π}{4})$ .

B.

(\frac{π}{2}; π)

.

C.

(π; \frac{3 π}{2})

.

D.

(\frac{3 π}{2}; 2 π)

.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 139

Trong các hàm số sau, hàm số nào đồng biến trên khoảng $(- \frac{π}{3}; \frac{π}{6})$ ?

A. $y = \tan (2 x + \frac{π}{6})$ .

B. $y = \cot (2 x + \frac{π}{6})$ .

C. $y = \sin (2 x + \frac{π}{6})$ .

D. $y = \cos (2 x + \frac{π}{6})$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 140

Đồ thị hàm số $y = \cos (x - \frac{π}{2})$ được suy từ đồ thị $(C)$ của hàm số $y = \cos x$ bằng cách:

A. Tịnh tiến $(C)$ qua trái một đoạn có độ dài là $\frac{π}{2} .$

B. Tịnh tiến $(C)$ qua phải một đoạn có độ dài là $\frac{π}{2} .$

C. Tịnh tiến $(C)$ lên trên một đoạn có độ dài là $\frac{π}{2} .$

D. Tịnh tiến $(C)$ xuống dưới một đoạn có độ dài là $\frac{π}{2} .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 141

Đồ thị hàm số $y = \sin x$ được suy từ đồ thị $(C)$ của hàm số $y = \cos x$ bằng cách:

A. Tịnh tiến $(C)$ qua trái một đoạn có độ dài là $\frac{π}{2} .$

B. Tịnh tiến $(C)$ qua phải một đoạn có độ dài là $\frac{π}{2} .$

C. Tịnh tiến $(C)$ lên trên một đoạn có độ dài là $\frac{π}{2} .$

D. Tịnh tiến $(C)$ xuống dưới một đoạn có độ dài là $\frac{π}{2} .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 142

Đồ thị hàm số $y = \sin x$ được suy từ đồ thị $(C)$ của hàm số $y = \cos x + 1$ bằng cách:

A. Tịnh tiến $(C)$ qua trái một đoạn có độ dài là $\frac{π}{2}$ và lên trên 1 đơn vị.

B. Tịnh tiến $(C)$ qua phải một đoạn có độ dài là $\frac{π}{2}$ và lên trên 1 đơn vị.

C. Tịnh tiến $(C)$ qua trái một đoạn có độ dài là $\frac{π}{2}$ và xuống dưới 1 đơn vị.

D. Tịnh tiến $(C)$ qua phải một đoạn có độ dài là $\frac{π}{2}$ và xuống dưới 1 đơn vị.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 143

Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.

Hỏi hàm số đó là hàm số nào?

A. $y = 1 + \sin 2 x .$

B. $y = \cos x .$

C. $y = - \sin x .$

D. $y = - \cos x .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 144

Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.

Hỏi hàm số đó là hàm số nào?

A. $y = \sin \frac{x}{2} .$

B. $y = \cos \frac{x}{2} .$

C. $y = - \cos \frac{x}{4} .$

D. $y = \sin (- \frac{x}{2}) .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 145

Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.

Hỏi hàm số đó là hàm số nào?

A. $y = \cos \frac{2 x}{3} .$

B. $y = \sin \frac{2 x}{3} .$

C. $y = \cos \frac{3 x}{2} .$

D.

y = \sin \frac{3 x}{2} .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 146

Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C,D

Hỏi hàm số đó là hàm số nào?

A.

y = \sin (x - \frac{π}{4}) .

B.

y = \cos (x + \frac{3 π}{4}) .

C.

y = \sqrt{2} \sin (x + \frac{π}{4}) .

D.

y = \cos (x - \frac{π}{4}) .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 147

Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.

Hỏi hàm số đó là hàm số nào?

A.

y = \sin (x - \frac{π}{4}) .

B. $y = \cos (x - \frac{π}{4}) .$

C.

y = \sqrt{2} \sin (x + \frac{π}{4}) .

D.

y = \sqrt{2} \cos (x + \frac{π}{4}) .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 148

Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.

Hỏi hàm số đó là hàm số nào?

A. $y = \sin x .$

B. $y = |\sin x| .$

C. $y = \sin |x| .$

D.

y = - \sin x .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 149

Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.

Hỏi hàm số đó là hàm số nào?

A. $y = \cos x .$

B. $y = - \cos x$

C. $y = \cos |x| .$

D.

y = |\cos x| .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 150

Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.

Hỏi hàm số đó là hàm số nào?

A. $y = |\sin x| .$

B. $y = \sin |x| .$

C. $y = \cos |x| .$

D.

y = |\cos x| .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 151

Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.

Hỏi hàm số đó là hàm số nào?

A. $y = \tan x .$

B. $y = \cot x .$

C. $y = |\tan x| .$

D.

y = |\cot x| .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 152

Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.

Hỏi hàm số đó là hàm số nào?

A.

y = \sin (x - \frac{π}{2}) - 1.

B.

y = 2 \sin (x - \frac{π}{2}) .

C.

y = - \sin (x - \frac{π}{2}) - 1.

D. $y = \sin (x + \frac{π}{2}) + 1.$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 153

Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.

Hỏi hàm số đó là hàm số nào?

A. $y = 1 + \sin |x| .$

B. $y = |\sin x|$ .

C.

y = 1 + |\cos x|

D.

y = 1 + |\sin x|

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 154

Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.

Hỏi hàm số đó là hàm số nào?

A. $y = 1 + \sin |x| .$

B. $y = |\sin x|$ .

C. $y = 1 + |\cos x|$ .

D. $y = 1 + |\sin x|$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 155

Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số $y = 3 \sin x - 2.$

A.

M = 1, m = - 5.

B. $M = 3, m = 1.$

C.

M = 2, m = - 2.

D.

M = 0, m = - 2.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 156

Tìm tập giá trị T của hàm số $y = 3 \cos 2 x + 5.$

A. $T = [- 1; 1] .$

B. $T = [- 1; 11] .$

C. $T = [2; 8] .$

D.

T = [5; 8] .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 157

Tìm tập giá trị T của hàm số $y = 5 - 3 \sin x .$

A. $T = [- 1; 1] .$

B. $T = [- 3; 3] .$

C. $T = [2; 8] .$

D. $T = [5; 8] .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 158

Cho hàm số $y = - 2 \sin (x + \frac{π}{3}) + 2$ . Mệnh đề nào sau đây là đúng?

A.

y \geq - 4, \forall x \in ℝ .

B.

y \geq 4, \forall x \in ℝ .

C.

y \geq 0, \forall x \in ℝ .

D.

y \geq 2, \forall x \in ℝ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 159

Hàm số $y = 5 + 4 \sin 2 x \cos 2 x$ có tất cả bao nhiêu giá trị nguyên?

A. 3

B.4

C.5

D.6

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 160

Tìm giá trị nhỏ nhất m của hàm số $y = - \sqrt{2} \sin (2016 x + 2017)$ .

A. $m = - 2016 \sqrt{2} .$

B. $m = - \sqrt{2} .$

C. $m = - 1.$

D. $m = - 2017 \sqrt{2} .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 161

Tìm giá trị nhỏ nhất m của hàm số $y = \frac{1}{\cos x + 1} .$

A. $m = \frac{1}{2} .$

B. $m = \frac{1}{\sqrt{2}} .$

C. $m = 1.$

D.

m = \sqrt{2} .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 162

Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \sin x + \cos x$ . Tính $P = M - m .$

A. $P = 4.$

B. $P = 2 \sqrt{2} .$

C. $P = \sqrt{2} .$

D. $P = 2.$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 163

Tập giá trị T của hàm số $y = \sin 2017 x - \cos 2017 x .$

A. $T = [- 2; 2] .$

B. $T = [- 4034; 4034] .$

C. $T = [- \sqrt{2}; \sqrt{2}] .$

D.

T = [0; \sqrt{2}] .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 164

Hàm số $y = \sin (x + \frac{π}{3}) - \sin x$ có tất cả bao nhiêu giá trị nguyên?

A.1

B.2

C.3

D.4

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 165

Hàm số $y = \sin^{4} x - \cos^{4} x$ đạt giá trị nhỏ nhất tại $x = x_{0}$ . Mệnh đề nào sau đây là đúng?

A.

x_{0} = k 2 π, k \in ℤ .

B. $x_{0} = k π, k \in ℤ .$

C.

x_{0} = π + k 2 π, k \in ℤ .

D. $x_{0} = \frac{π}{2} + k π, k \in ℤ .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 166

Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số $y = 1 - 2 |\cos 3 x| .$

A.

M = 3, m = - 1.

B.

M = 1, m = - 1.

C.

M = 2, m = - 2.

D.

M = 0, m = - 2.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 167

Tìm giá trị lớn nhất M của hàm số $y = 4 \sin^{2} x + \sqrt{2} \sin (2 x + \frac{π}{4}) .$

A. $M = \sqrt{2} .$

B. $M = \sqrt{2} - 1.$

C. $M = \sqrt{2} + 1.$

D. $M = \sqrt{2} + 2.$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 168

Tìm tập giá trị T của hàm số $y = \sin^{6} x + \cos^{6} x .$

A. $T = [0; 2] .$

B. $T = [\frac{1}{2}; 1] .$

C. $T = [\frac{1}{4}; 1] .$

D.

T = [0; \frac{1}{4}] .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 169

Cho hàm số $y = \cos^{4} x + \sin^{4} x$ . Mệnh đề nào sau đây là đúng?

A. $y \leq 2, \forall x \in ℝ .$

B. $y \leq 1, \forall x \in ℝ .$

C.

y \leq \sqrt{2}, \forall x \in ℝ .

D. $y \leq \frac{\sqrt{2}}{2}, \forall x \in ℝ .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 170

Hàm số $y = 1 + 2 \cos^{2} x$ đạt giá trị nhỏ nhất tại $x = x_{0}$ . Mệnh đề nào sau đây là đúng?

A.

x_{0} = π + k 2 π, k \in ℤ .

B.

x_{0} = \frac{π}{2} + k π, k \in ℤ .

C.

x_{0} = k 2 π, k \in ℤ .

D.

x_{0} = k π, k \in ℤ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 171

Tìm giá trị lớn nhất M và nhỏ nhất m của hàm số $y = \sin^{2} x + 2 \cos^{2} x .$

A. $M = 3, m = 0.$

B. $M = 2, m = 0.$

C. $M = 2, m = 1.$

D.

M = 3, m = 1.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 172

Tìm giá trị lớn nhất M của hàm số $y = \frac{2}{1 + \tan^{2} x} .$

A. $M = \frac{1}{2} .$

B.

M = \frac{2}{3} .

C.

M = 1.

D.

M = 2.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 173

Gọi m,M lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = 8 \sin^{2} x + 3 \cos 2 x$ . Tính $P = 2 M - m^{2} .$

A.

P = 1.

B.

P = 2.

C.

P = 112.

D.

P = 130.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 174

Tìm giá trị nhỏ nhất m của hàm số $y = 2 \sin^{2} x + \sqrt{3} \sin 2 x$ .

A.

m = 2 - \sqrt{3} .

B. $m = - 1.$

C.

m = 1.

D.

m = - \sqrt{3} .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 175

Tìm tập giá trị T của hàm số $y = 12 \sin x - 5 \cos x .$

A. $T = [- 1; 1] .$

B. $T = [- 7; 7] .$

C. $T = [- 13; 13] .$

D.

T = [- 17; 17] .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 176

Tìm giá trị lớn nhất M của hàm số $y = 4 \sin 2 x - 3 \cos 2 x .$

A.

M = 3.

B.

M = 1.

C.

M = 5.

D.

M = 4.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 177

Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \sin^{2} x - 4 \sin x + 5$ . Tính $P = M - 2 m^{2} .$

A.

P = 1.

B.

P = 7.

C.

P = 8.

D. $P = 2.$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 178

Hàm số $y = \cos^{2} x - \cos x$ có tất cả bao nhiêu giá trị nguyên?

A.1

B.2

C.3

D.4

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 179

Hàm số $y = \cos^{2} x + 2 \sin x + 2$ đạt giá trị nhỏ nhất tại $x_{0}$ . Mệnh đề nào sau đây là đúng?

A.

x_{0} = \frac{π}{2} + k 2 π, k \in ℤ .

B.

x_{0} = - \frac{π}{2} + k 2 π, k \in ℤ .

C.

x_{0} = π + k 2 π, k \in ℤ .

D.

x_{0} = k 2 π, k \in ℤ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 180

Tìm giá trị lớn nhất M và nhất m của hàm số $y = \sin^{4} x - 2 \cos^{2} x + 1$

A.

M = 2, m = - 2.

B.

M = 1, m = 0.

C.

M = 4, m = - 1.

D.

M = 2, m = - 1.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 181

Tìm giá trị nhỏ nhất m của hàm số $y = 4 \sin^{4} x - \cos 4 x$ .

A. $m = - 3.$

B. $m = - 1.$

C. $m = 3.$

D.

m = - 5.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 182

Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số $y = \sqrt{7 - 3 \cos^{2} x} .$

A.

M = \sqrt{10}, m = 2.

B.

M = \sqrt{7}, m = 2.

C.

M = \sqrt{10}, m = \sqrt{7} .

D.

M = 0, m = 1.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 183

Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ t của năm 2017 được cho bởi một hàm số $y = 4 \sin [\frac{π}{178} (t - 60)] + 10$ với $t \in ℤ$ và $0 < t \leq 365$ . Vào ngày nào trong năm thì thành phố A có nhiều giờ có ánh sáng mặt trời nhất?

A. 28 tháng 5.

B. 29 tháng 5.

C. 30 tháng 5.

D. 31 tháng 5

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 184

Hằng ngày mực nước của con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mực nước trong kênh được tính tại thời điểm t (giờ) trong một ngày bởi công thức $h = 3 \cos (\frac{π t}{8} + \frac{π}{4}) + 12.$ Mực nước của kênh cao nhất khi:

A.13 (giờ).

B.14 (giờ).

C.15 (giờ).

D.16 (giờ).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP